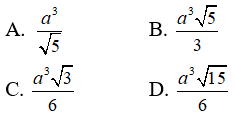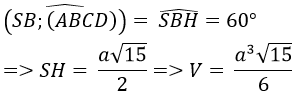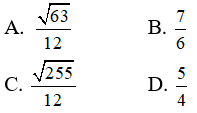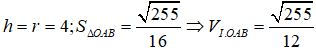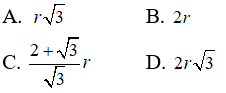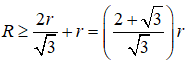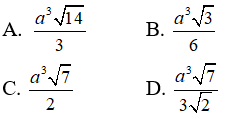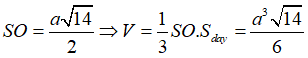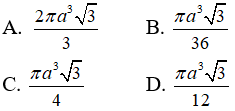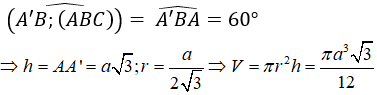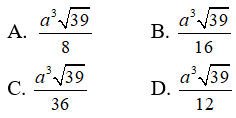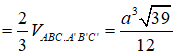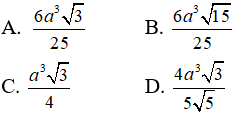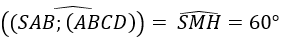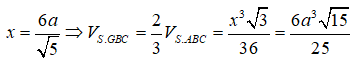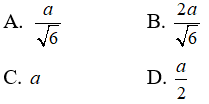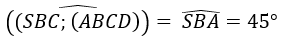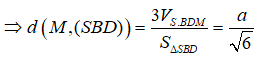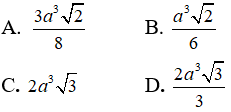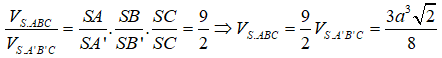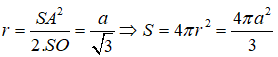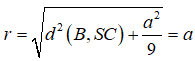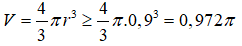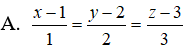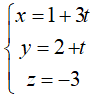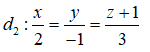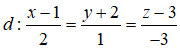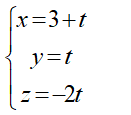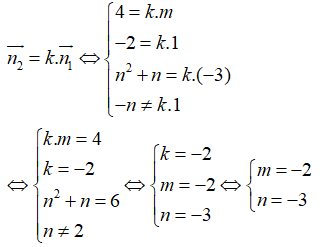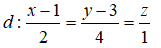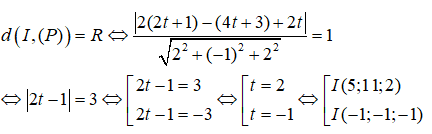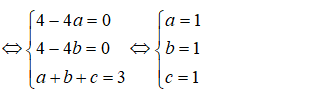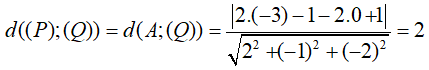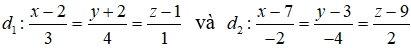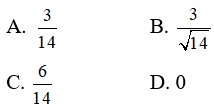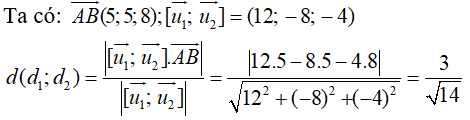Câu 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác cân tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy là 60^o . Tính thể tích khối chóp S.ABCD

Gọi H là trung điểm của AD, khi đó từ giả thiết ta có SH ⊥ (ABCD) . Ta có :

Câu 2: Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao của hình nón. Giả sử khoảng cách từ trung điểm của IO tới một đường sinh bất kì là √2 . Hai điểm A, B nằm trên đường tròn tâm O sao cho AB = 1/2. Tính thể tích khối tứ diện IABO

Từ giả thiết ta suy ra :

Câu 3: Có ba quả bóng đá hình cầu có cùng bán kính r được xếp tiếp xúc với nhau từng đôi một. Trong các rổ hình trụ có chiều cao 2r và bán kính R, hỏi bán kính R nhỏ nhất là bao nhiêu để hình trụ có thể chứa được cả ba quả bóng đó?

Do chiều cao của hình trụ là 2r nên để đựng được ba quả cầu trong hình trụ thì ba quả đó phải chạm đáy hình trụ. Khi đó gọi A,B,C là ba tâm của ba quả cầu thì tam giác ABC đều và bán kính R không nhỏ hơn bán kính đường tròn ngoại tiếp tam giác ABC cộng với bán kính r. Tam giác ABC có cạnh 2r nên ta có:

Câu 4: Trong không gian Oxyz, cho ba điểm A(1; 2; 0), B(-2; 1; 3), C(7; -3; -6). Viết phương trình tham số của đường thẳng d đi qua trọng tâm G của tam giác ABC, đồng thời d song song với hai mặt phẳng (Oxy) và (Oxz)

A. x = 2 + t, y = 0, z = -1   

B. x = -2 + t, y = 0, z = -1

C. x = 1 + 2t, y = 0, z = -t   

D. x = 6 + t, y = 0, z = -3

Câu 5: Một hình chóp có 40 cạnh. Hình chóp đó có bao nhiêu mặt?

A. 20   

B. 21   

C. 22   

D. 40

Gọi hình chóp đã cho là hình chóp n – giác, khi đó số cạnh của hình chóp là 2n=40. Suy ra n=20 và do đó số mặt của hình chóp là n+1=21

Câu 6: Trong số các mệnh đề sau đây, mệnh đề nào đúng?

A. Số cạnh của một hình đa diện luôn là một số chẵn

B. Số mặt của một hình đa diện luôn là một số chẵn

C. Số đỉnh của một hình lăng trụ luôn là một số chẵn

D. Số cạnh của một hình lăng trụ luôn là một số chẵn

Hình lăng trụ tam giác có 9 cạnh nên mệnh đề A và D sai. Hình chóp tứ giác có 5 mặt nên mệnh đề B sai. Lăng trụ n-giác có 2n đỉnh nên đáp án đúng là C.

Câu 7: Trong các mệnh đề sau đây, mệnh đề nào sai?

A. Tồn tại các khối đa diện đều loại (3;4)

B. Tồn tại các khối đa diện đều loại (5;3)

C. Tồn tại các khối đa diện đều loại (3;5)

D. Tồn tại các khối đa diện đều loại (4;4)

Trong bảng phân loại 5 khối đa diện đều ta không thấy có khối đa diện đều loại (4 ;4)

Câu 8: Trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Trong một hình đa diện đều, số đỉnh luôn lớn hơn số mặt

B. Tồn tại một hình đa diện đều có số đỉnh bằng số mặt

C. Trong một hình đa diện đều, số đỉnh luôn bằng số mặt

D. Trong một hình đa diện đều, số đỉnh luôn nhỏ hơn số mặt

Nhìn vào bảng phân loại 5 hình đa diện đều ta có đáp án đúng là B

Câu 9: Cho hình chóp tứ giác đều S.ABCD, cạnh đáy là a, SA = 2a. Thể tích khối chóp là:

Gọi O là tâm của đáy, khi đó ta có SO ⊥ (ABCD).

Diện tích đáy là: S = a²

Ta tính được:

Câu 10: Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = a , góc giữa A’B và mặt phẳng (ABC) là 60^o . Khối trụ (H) là khối trụ có hai đường tròn đáy lần lượt là đường tròn nội tiếp các tam giác ABC, A’B’C’. Tính thể tích khối trụ (H)

Từ giả thiết ta có :

Câu 11: Cho lăng trụ ABC.A'B'C' có độ dài cạnh bên bằng 2a, đáy ABC là tam giác đều cạnh a và hình chiếu vuông góc của đỉnh A’ trên mặt phẳng (ABC) là trung điểm cạnh BC. Thể tích khối chóp A.BCC’B’ là:

Gọi H là trung điểm của BC, khi đó từ giả thiết ta có A'H ⊥ (ABC). Ta có:

A'H = a√3 => V_A.BCC'B' = V_ABC.A'B'C' - V_A'.ABC

Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB = AC, SA = SB = SC = 3a. Góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) là 60^o . Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp S.GBC là:

Gọi H là chân đường vuông góc hạ từ đỉnh S lên mặt phẳng (ABC), khi đó ta chứng minh được H là trung điểm của BC. Gọi M là trung điểm của AB khi đó từ giả thiết ta có :

Đặt AB = x ta tính được :

Câu 13: Cho hình chóp S.ABCD có SA ⊥ (ABCD) , đáy ABCD là hình chữ nhật. SA = 2AD = 2a . Góc giữa mp(SBC) và mặt đáy là 45^o . Gọi M là trung điểm của BC. Khoảng cách từ M đến mp(SBD) là:

Từ giả thiết ta có :

=> AB = SA = 2a => V_S.BDM = (1/4)V_S.ABCD = a³/3

Mặt khác ta có :

SB = 2a√2; SD = a√5; BD = a√5 => S_ΔSBD = a²√6

Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là a³ . Tính thể tích khối chóp S.ABCD

A. a³   

B. 4a³   

C. 8a³    

D. 16a³

Từ giả thiết ta có :

=> AB = SA = 2a => V_S.BDM = (1/4)V_S.ABCD = a³/3

Mặt khác ta có :

SB = 2a√2; SD = a√5; BD = a√5 => S_ΔSBD = a²√6

Câu 15: Cho hình chóp S.ABC có ∠ASB = ∠BSC = ∠CSA = 60^o, SA = 2SB = 3SC = 3a Thể tích khối chóp S.ABC là :

Gọi A’,B’ lần lượt thuộc các cạnh SA, SB sao cho SA' = SB' = a. Khi đó SA’B’C’ là tứ diện đều cạnh bằng a. Theo công thức tỉ số thể tích ta có :

Câu 16: Cho hình chóp S.ABC có hình chiếu vuông góc của S lên mặt đáy là tâm O của đường tròn ngoại tiếp tam giác ABC. Biết SB = a và góc giữa cạnh bên SA và mặt đáy bằng 60^o . Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC là :

Từ giả thiết ta có SO là trục của đường tròn ngoại tiếp tam giác ABC và SA=SB=a. Trong mặt phẳng (SAO), trung trực của cạnh SA cắt SO tại I thì I là tâm của mặt cầu ngoại tiếp hình chóp. Khi đó ta tính được :

Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính của mặt cầu ngoại tâm B cắt SC theo một dây có độ dài 2a/3 là :

Từ giả thiết ta có SA ⊥ (ABCD), theo định lí ba đường vuông góc ta có tam giác SBC vuông tại B. Gọi S(B,r) là mặt cầu tâm B cắt SC theo một dây có độ dài 2a/3. Khi đó ta tính được:

Câu 18: Hình nón có thiết diện cắt bởi mặt phẳng qua trục là một tam giác vuông và có diện tích xung quanh là √2 . Độ dài đường cao của hình nón là :

A. √2    

B. 1   

C. 1/√2   

D. 2

Từ giả thiết ta có : 2α = 90^o => α = 45^o => h = r; l = r√2

Diện tích xung quanh của hình nón là : S_xq = πrl = πr²√2 = π√2 => r = 1 => h = 1

Câu 19: Bạn Nam cao 1,8m tham gia trò chơi nhà bóng. Bạn Nam phải đứng thẳng trong quả bóng hình cầu và lăn trên cỏ. Để Nam có thể đứng được trong quả bóng thì Nam phải chọn quả bóng có thể tích ít nhất là bao nhiêu trong các kết quả sau:

A. π(m³)   

B. 7,776π(m³)   

C. 2,916π(m³)   

D. 0,648π(m³)

Bạn Nam cao 1,8m nên đường kính của quả bóng không nhỏ hơn 1,8m hay bán kính không nhỏ hơn 0,9m. Do đó thể tích quả bóng thỏa mãn điều kiện là :

Câu 20: Cho hình trụ có thể tích bằng 2π và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Diện tích xung quanh của khối trụ là:

A. π   

B. 2π   

C. 4π/3   

D. 4π

Từ giả thiết ta có : h = 2r; V = πr²h = 2π => r = 1, h = 2 => S_xq = 2πrh = 4π

Câu 21: Trong không gian Oxyz, cho hai đường thẳng cắt nhau:d₁: x = 1 + t, y = 1, z = 1 - t, d₂: x = -t, y = 2 + t, z = 1. Viết phương trình của mặt phẳng (P) chứa hai đường thẳng d₁, d₂

A. x + y + z - 3 = 0    

B. x + y + z + 3 = 0  

C. x - y + z - 1 = 0  

D. x - y + z + 1 = 0

Đường thẳng d₁ đi qua A(1; 1; 1), vecto chỉ phương u₁→(1; 0; -1)

Đường thẳng d₂ đi qua B( 0; 2;1), vecto chỉ phương u₂→(-1; 1; 0)

Mặt phẳng (P) chứa hai đường thẳng d₁; d₂ nên nhận vecto [u₁→;u₂→] = (1; 1; 1) làm vecto pháp tuyến và đi qua A(1; 1; 1). Phương trình (P):

1(x - 1) + 1(y – 1) + 1(z - 1) = 0 hay x + y + z – 3= 0

Chọn A.

Câu 22: Cho một đồ chơi hình khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = 6cm. Trong tất cả các khối cầu có thể chứa đồ chơi đó thì khối cầu có bán kính nhỏ nhất là:

A. √6 (cm)   

B. 2√6 (cm)    

C. 3√3 (cm)   

D. 3√6 (cm)

Chọn hệ trục tọa độ Oxyz; trong đó điểm S(0; 0; 0); A(6; 0; 0); B(0; 6; 0) và C(0; 0; 6).

Tam giác ABC là tam giác đều: AB = BC = AC = 6√2

Xét mặt cầu tâm I, là tâm của tam giác đều ABC, và có bán kính r = 2√6, bằng bán kính đường tròn ngoại tiếp tam giác ABC.

Do I là tâm tam giác ABC nên I(2; 2; 2).

Khoảng cách 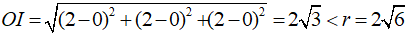 nên mặt cầu S(I,r) chứa hình chóp S.ABC. Đáp án đúng là B

Lưu ý. Lỗi thường gặp là chọn đáp án C vì đó là bán kính mặt cầu ngoại tiếp hình chóp S.ABC.

Câu 23: Trong không gian Oxyz, cho các điểm A(1;1;0), B(0;1;1). Tìm trên mặt phẳng xOz tọa độ điểm C để OABC là một tứ diện đều

A. C(0;0;1)   

B. C(1;0;0)   

C. C(1;0;1)   

D. C(2;0;2)

Dựng hình lập phương cạnh bằng 1, nhận O, A, B, C làm các đỉnh.

Câu 24: Trong không gian Oxyz, cho mặt cầu (S) có phương trình x² + y² + z² = 1. Viết phương trình mặt phẳng (P) đi qua

và tiếp xúc với (S)

A. √3x + 4z - 2 = 0   

B. √3y + z - 2 = 0

C. y + √3z = 0    

D. x + √3y + z - 2 = 0

Câu 25: Trong không gian Oxyz, cho ba điểm A(1; -2; 3), B(0; 1; 5), C(4; -1; 7). Gọi M là trung điểm của BC. Viết phương trình tham số của đường thẳng AM

B. x = -1 + t, y = 2 + 2t, z = -3 + 3t

C. x = 1 + t, y = 2 - 2t, z = 3 + 3t

D. x = 1 + t, y = -2 + 2t, z = 3 + 3t

Câu 26: Trong không gian Oxyz, viết phương trình tham số của đường thẳng d đi qua điểm M(1;2;-3) và d vuông góc với mặt phẳng (P): 3x + y + 1 = 0

A. x = -1 - 3t, y = -2 - t, z = 3   

B. x = 1 + 3t, y = 2 + t, z = -3 + t 

C. x = 3 + t, y = 1 + 2t, z = -3t  

D. x = 1 + 3t, y = 2 + t, z = -3

Mặt phẳng (P) có vecto pháp tuyến là: n_p→(3; 1; 0)

Vì đường thẳng d vuông góc với mặt phẳng (P) nên đường thẳng d có vecto chỉ phương là: u_d→ = n_p→(3; 1; 0)

Phương trình tham số của đường thẳng d:

Chọn D.

Câu 27: Trong không gian Oxyz, viết phương trình của mặt phẳng (P) chứa hai đường thẳng sau: d₁: x = 3 + 4t, y = 1 - 2t, z = 3 + 6t và

A. 7x + y - 5z - 5 = 0    

B. 7x - y - 5z - 5 = 0

C. 2x - y + 3z + 3 = 0    

D. 3x + y + 3z - 5 = 0

Câu 28: Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6) và ba điểm B, C, D cùng thuộc mặt phẳng (Oyz). Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. Lập phương trình mặt phẳng (MNP)

A. x + 1 = 0   

B. x - 1 = 0

C. y + z - 1 = 0   

D. x = 1 + t, y = -2, z = 3

* Tam giác ABC có MN là đường trung bình nên MN// BC (1)

Tam giác ACD có NP là đường trung bình nên NP // CD (2)

Từ (1) và (2) suy ra: (MNP) song song mp( BCD) hay (MNP) song song mp(Oyz).

* Mà mặt phẳng (Oyz) có 1 vecto pháp tuyến là i→(1; 0; 0) nên mặt phẳng (MNP) có VTPT i→(1; 0; 0).

* Điểm O(0; 0; 0). Gọi I(1; -2; 3) là trung điểm của AO. Suy ra; điểm I thuộc mặt phẳng (MNP).

* Phương trình mặt phẳng (MNP) là:

1(x- 1) + 0(y+ 2) + 0( z- 3) =0 hay x- 1= 0

Chọn B.

Câu 29: Trong không gian Oxyz, cho đường thẳng d và mặt phẳng (P) lần lượt có phương trình là:

(P): 2x + y - 3z - 4 = 0. Trong những khẳng định dưới đây, khẳng định nào đúng?

A. d nằm trong mặt phẳng (P)   

B. d song song với mặt phẳng (P)

C. d không vuông góc với mặt phẳng (P)   

D. d cắt mặt phẳng (P)

Ta có vectơ chỉ phương của đường thẳng d là : u_d→ = (2; 1; -3), đồng thời n_P→ = (2; 1; -3) = u_d→ cũng là vectơ pháp tuyến của mặt phẳng (P). Do đó đường thẳng d vuông góc với mặt phẳng (P), suy ra đường thẳng d cắt mặt phẳng (P).

Câu 30: Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6), B(1;1;1), C(0;3;0), D(0;0;3). Viết phương trình tham số của đường thẳng d chứa đường cao AH của tứ diện ABCD

A. x = 2 + t, y = -4 - t, z = 6 + t    

B. x = 1 + 2t, y = -1 -4t, z = 1 + 6t 

C. x = 2 + t, y = -4 + t, z = 6 + t  

D. x = 1 + 2t, y = 1 - 4t, z = 1 + 6t

Câu 31: Trong không gian Oxyz, cho hai điểm A(3;2;1), M(3;0;0) và mặt phẳng (P) có phương trình là: x + y + z - 3 = 0 . Viết phương trình của đường thẳng d đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ A đến đường thẳng d nhỏ nhất

A. x = -3 - t, y = t, z = 0    

B. x = 3 + t, y = 2t, z = 2t

C. x = 3 - t, y = t, z = 0    

D. Đáp án khác

Gọi H là hình chiếu của A trên đường thẳng d.

Ta có: AH ≤ AM nên khoảng cách từ A đến đường thẳng d nhỏ nhất khi AH trùng với mới AM, khi đó H trùng với M và AM vuông góc d. Mặt phẳng (P) có vecto pháp tuyến n_p→(1; 1; 1) . AM→(0; -2; -1) Đường thẳng d nhận vecto [AM→;n_p→] làm vecto chỉ phương. Phương trình tham số của d:

Chọn D

Câu 32: Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là mx + y - 3z + 1 = 0; 4x - 2y + (n² + n)z - n = 0, trong đó m và n là hai tham số. Với những giá trị nào của m và n thì hai mặt phẳng (P) và (Q) song song với nhau

A. m=-2 và n=2    

B. m=2 và n=-3

C. m=-2 và n=2 hoặc n=-3    

D. m=-2 và n=-3

Hai mặt phẳng đã cho song song khi và chỉ khi tồn tại một số thực k sao cho :

Câu 33: Trong không gian Oxyz, cho đường thẳng

và mặt phẳng (P): 2x - y + 2z = 0. Cho mặt cầu (S) có tâm I thuộc đường thẳng d, có bán kính bằng 1 và tiếp xúc với mặt phẳng (P). Tọa độ tất cả các điểm I có thể là:

A. I₁(5; 11; 2)   

B. I₂(3; 7; 1) 

C. I₂(3; 7; 1) hoặc I₃(-3; -5; -2)  

D. I₁(5; 11; 2) hoặc I₄(-1; -1; -1)

Phương trình tham số của đường thẳng d là : d: x = 1 +2 t, y = 3+ 4t, z = t

Ta có I ∈ d => I(1 + 2t, 3 + 4t, t). Vì (S) tiếp xúc với mặt phẳng (P) nên ta có :

Câu 34: Trong không gian Oxyz, lập phương trình của mặt cầu (S) đi qua 3 điểm O, A(2;0;0), B(0;2;0) và tâm thuộc mặt phẳng (P): x + y + z - 3 = 0

A. (x - 1)² + (y - 1)² + (z - 1)² = 3    

B. (x + 1)² + (y + 1)² + (z + 1)² = 3

C. (x - 1)² + (y - 1)² + (z - 1)² = 9   

D. (x + 1)² + (y + 1)² + (z + 1)² = 9

Gọi I(a,b,c) là tâm của mặt cầu (S). Ta có:

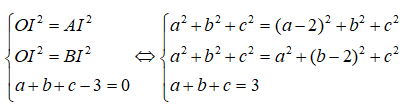
=> I(1; 1; 1); R = OI = √3

Vậy phương trình của mặt cầu (S) là: (x - 1)² + (y - 1)² + (z - 1)² = 3

Câu 35: Trong không gian Oxyz, cho bốn điểm A(1;0;0), B(0;-2;0), C(0;0;2), M(1;1;4). Tính khoảng cách từ M đến mặt phẳng (ABC)

A. 0   

B. √6/2   

C. 1/2   

D. 2

Câu 36: Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 = 0, (Q): 2x - y - 2z + 1 = 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu?

A. 4π   

B. π   

C. 2π    

D. 16π

Hai mặt phẳng (P) và (Q) có cùng vecto pháp tuyến là: n→(2; -1; -2)

Điểm A(-3; 1; 0) thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q).

Do đó, hai mặt phẳng (P) và (Q) song song với nhau.

Khoảng cách giữa hai mặt phẳng là:

Vì mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q) nên khoảng cách giữa hai mặt phẳng (P) và (Q) chính là đường kính của mặt cầu:

2R = 2 nên R = 1.

Diện tích của mặt cầu (S) là: S = 4πR² = 4 π

Câu 37: Trong không gian Oxyz, cho hai đường thẳng:

Cho M là một điểm di động trên d₁ , N là một điểm di động trên d₂ . Khoảng cách nhỏ nhất của đoạn thẳng MN là:

* Với M là một điểm di động trên d₁ , N là một điểm di động trên d₂ thì MN ≤ d(d₁; d₂)

Do đó, khoảng cách nhỏ nhất của MN chính là khoảng cách giữa hai đường thẳng d1 và d2. Khi đó, MN là đoạn vuông góc chung của hai đường thẳng đã cho.

* Đường thẳng d₁ đi qua A(2; -2; 1), vecto chỉ phương u₁→(3; 4; 1)

Đường thẳng d₂ đi qua B(7;3;9) vecto chỉ phương u₂→(-2; -4; 2)

Ta có:

Chọn B.