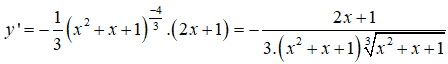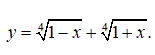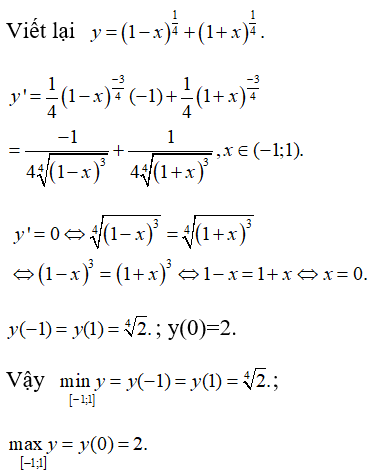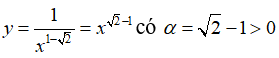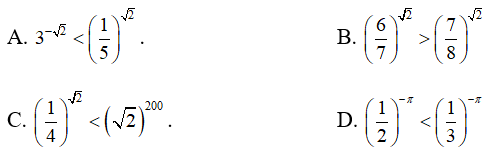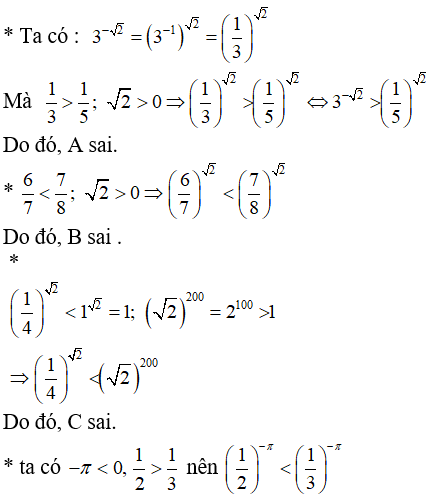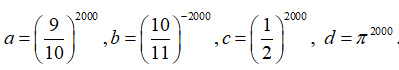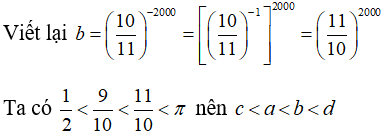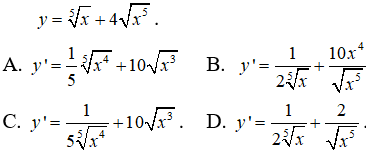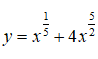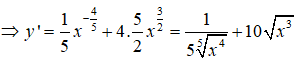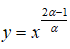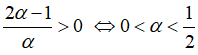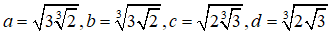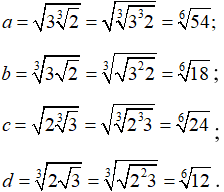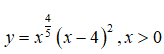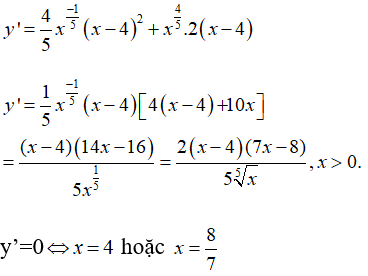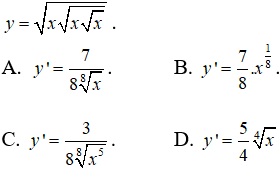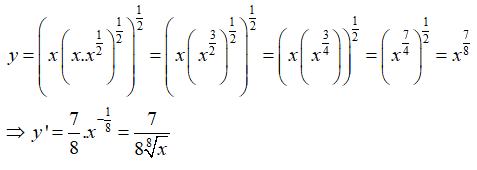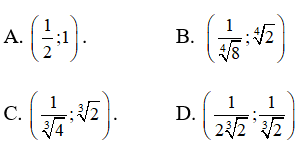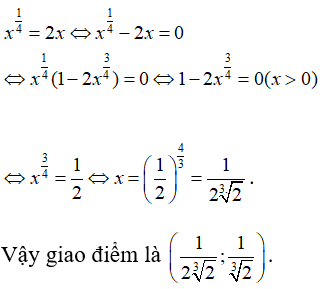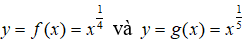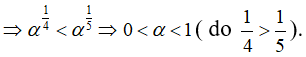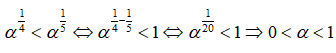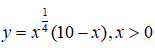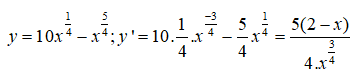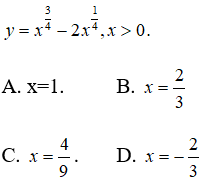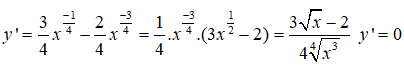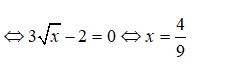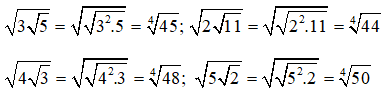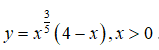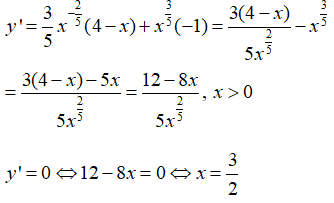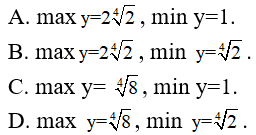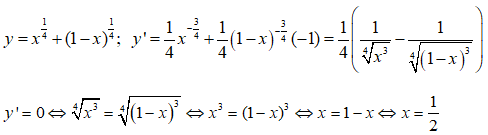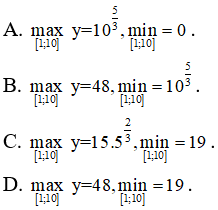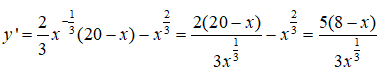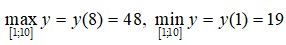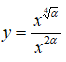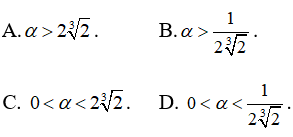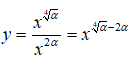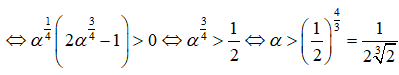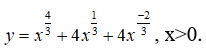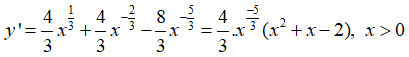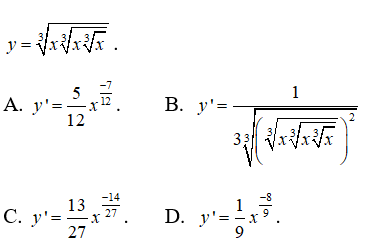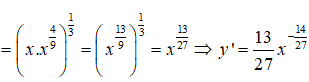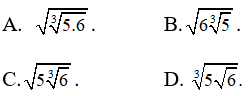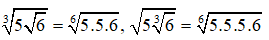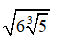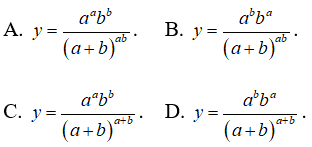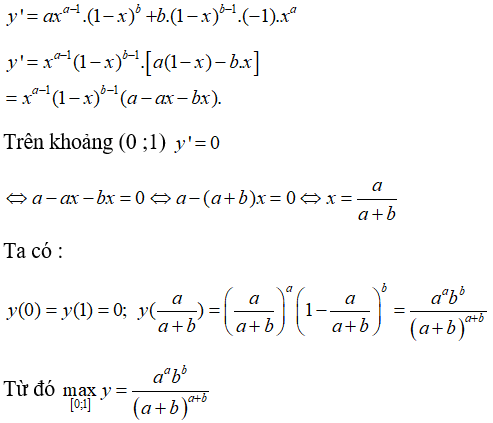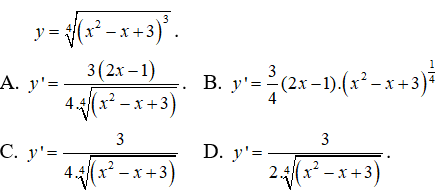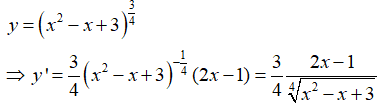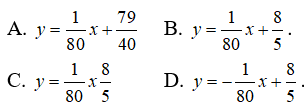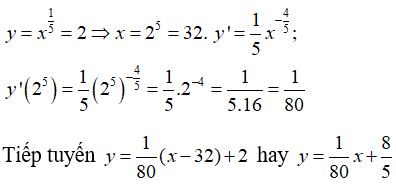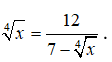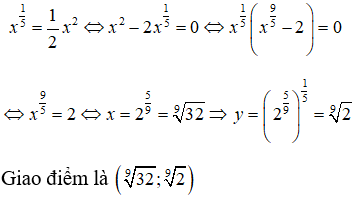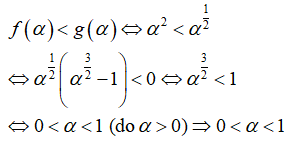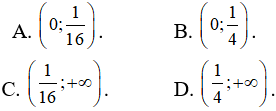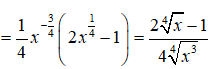Bài 1: Tìm đạo hàm của hàm số

Viết lại hàm số dưới dạng lũy thừa y = (x² + x + 1)^-1/3 .

Sử dụng công thức đạo hàm hàm hợp ta có

Chọn đáp án B.

Bài 2: Tìm giá trị lớn nhất và nhỏ nhất của hàm số

A. max y = 2√2 , min y = ∜2 .   

B.max y=2, min y=0.

C. max y = 2√2 , min y=0   

D.max y=2, min y= ∜2 .

Tập xác định D = [-1;1].

Chọn đáp án D

Bài 3: Hàm số nào sau đây đồng biến trên (0; +∞) ?

Hàm số y = x^α đồng biến trên (0; +∞) khi và chỉ khi α > 0 .

Hàm số 

nên hàm số đồng biến trên (0; +∞).

Chọn C.

Bài 4: Khẳng định nào sau đây là đúng?

Viết lại sao cho hai vế của mỗi bất đẳng thức đều là lũy thừa cùng số mũ. Lưu ý, từ tính đơn điệu của hàm số lũy thừa y = x^α , ta có

• Nếu α > 0 thì a^α < b^α ⇔ a < b

• Nếu α < 0 thì a < b ⇒ a^α > b^α

Suy ra, D đúng.

Chọn D

Bài 5: Số nào sau đây là lớn hơn 1?

Lưu ý với

Do đó, trong các số đã cho thì (0,4)^-0,3 > 1

Chọn B.

Bài 6: Sắp xếp các số theo thứ tự tăng dần:

A. d,c,a,b.   

B.d,c,b,a.   

C. c,d,b,a.   

D.c,a,b,d.

Bài 7: Tìm đạo hàm của hàm số

Bài 8: Cho α là một số thực và hàm số 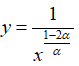 đồng biến trên (0; +∞). Khẳng định nào sau đây là đúng

A. α < 1    

B. 0 < α < 1/2    

C. 1/2 < α < 1   

D. α > 1

Hàm số đồng biến khi và chỉ khi

Chọn đáp án B

Bài 9: Sắp xếp các số sau theo thứ tự tăng dần:

A. b,c,d,a    

B. a,b,c,d    

C.c,d,a,b.   

D. d,b,c,a.

Viết lại các số dưới dạng cùng căn bậc 6:

Do 12 < 18 < 24 < 54 nên d < b < c < a các số theo thứ tự tăng dần là d,b,c,a.

Chọn đáp án D.

Bài 10: Tìm các điểm cực trị của hàm số

A. x=4 và x = 8/7 .   

B. x=4.   

C. x=2.    

D. x=2 và x = 4/9 .

Ta thấy y’ đổi dấu khi đi qua 2 điểm x=4 và x = 8/7 nên đây là 2 điểm cực trị của các hàm số đã cho.

Chọn đáp án A.

Bài 11: Tìm đạo hàm của hàm số

Viết lại hàm số dưới dạng lũy thừa

Đáp án A.

Bài 12: Đồ thị hàm số y = x^1/4 cắt đường thẳng y=2x tại một điểm nằm bên phải trục tung. Tìm tọa độ điểm này.

Phương trình hoành độ giao điểm

Chọn đáp án D.

Bài 13: Đường thẳng x = α ( α là số thực dương) cắt đồ thị các hàm số

lần lượt tại hai điểm A và B. Biết rằng tung độ điểm A bé hơn tung độ điểm B. Khẳng định nào sau đây là đúng?

A. 0 < α < 1    

B. α > 1   

C. 1/5 < α < 4   

D. 1/4 < α < 5

Từ giả thiết suy ra f(α) < g(α)

Chọn đáp án A.

Nhận xét. Ở đây ta sử dụng tính chất:

Nếu a > 1 thì a^α > a^β <=> α > β ;

Nếu 0 < a < 1 thì a^α > a^β <=> α < β .

Học sinh có thể không áp dụng tính chất trên mà giải tiếp:

Bài 14: Cho hàm số

Khẳng định nào sau đây là đúng?

A. Hàm số nghịch biến trên (0;2).

B. Hàm số nghịch biến trên khoảng (5; +∞) .

C. Hàm số đồng biến trên (2; +∞) .

D. Hàm số không có điểm cực trị nào.

Ta có

Ta thấy y'(x) < 0 <=> x > 2 nên hàm số nghịch biến trên (2; +∞) , và do đó, hàm số nghịch biến trên (5; +∞) .

Chọn đáp án B.

Bài 15: Tìm các điểm cực trị của hàm số

y’ đổi dấu khi qua điểm x = 4/9 nên hàm số có một điểm cực trị là x = 4/9 .

Chọn đáp án C.

Bài 16: Số nào lớn nhất trong các số được liệt kê trong bốn phương án A,B,C,D dưới đây?

Viết lại các số dưới dạng cùng căn bậc 4:

Từ đó ta thấy 5√2 là lớn nhất

Bài 17: Tìm các điểm cực trị của hàm số

A. x=2.   

B. 3/2   

C. x=6.   

D. x=4.

y’ đổi dấu khi đi qua điểm x = 3/2 nên hàm số có một điểm cực trị là x = 3/2

Bài 18: Tìm các giá trị lớn nhất và nhỏ nhất của hàm số 

Tập xác định D = [0; 1]

Ta có:

y(0) = y(1) = 1; y(1/2) = ∜8. Từ đó max y = y(1/2) = ∜8, min y = y(0) = 1

Bài 19: Tìm các giá trị lớn nhất và nhỏ nhất của hàm số y = x^2/3(20 - x) trên đoạn [1; 10]

y' = 0 <=> x = 8

Ta có: y(1) = 19, y(8) = 48, y(10) = 10^5/3 ≈ 46,6 > 19

Từ đó:

Bài 20: Với là một số thực dương và hàm số

nghịch biến trên khoảng (0; +∞). Khẳng định nào sau đây là đúng?

Hàm số

nghịch biến trên (0; +∞) nên ∜α - 2α < 0

Bài 21: Tìm các điểm cực trị của hàm số

A. x=1.   

B.x=2.

C. x=1 va x=-2   

D. x=2 và x=-1.

y'= 0 <=> x² + x - 2 = 0 <=> x = -2 (loại) hoặc x = 1

y' đổi dấu khi đi qua điểm x = 1 nên hàm số có một điểm cực trị là x = 1

Bài 22: Tìm đạo hàm của hàm số

Viết lại

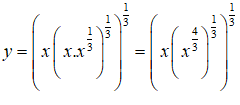
Bài 23: Số nào lớn nhất trong các số được liệt kê trong bốn phương án A,B,C,D dưới đây?

Viết lại các số

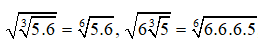
Từ đó ta thấy số lớn nhất là

Bài 24: Cho a và b là hai số dương. Tìm giá trị lớn nhất của hàm số y = x^a(1 - x)^b trên [0;1].

Bài 25: Tìm đạo hàm của hàm số

Viết lại:

Bài 26: Viết phương trình tiếp tuyến của đồ thị hàm số y = x^1/5 tại điểm có tung độ bằng 2.

Bài 27: Tính tổng các nghiệm của phương trình

A. 7.   B. 25.    C. 73.     D.337.

Tổng hai nghiệm : 81 + 256 = 337

Bài 28: Tìm tọa độ giao điểm của đồ thị

Phương trình hoành độ giao điểm

Bài 29: Cho 2 hàm số f(x) = x² và g(x) = x^1/2 . Biết rằng α > 0, f(α) < g(α). Khẳng định nào sau đây là đúng?

A. 0 < α < 1/2    

B. 0 < α < 1   

C. 1/2 < α < 2   

D. α > 1

Bài 30: Tìm các khoảng đồng biến của hàm số y = √x - ∜x, x > 0

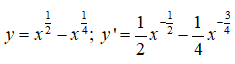
y' = 0 <=> 2∜x - 1 > 0 <=> x > 1/16 => Khoảng đồng biến của hàm số là (1/16; +∞)