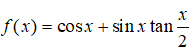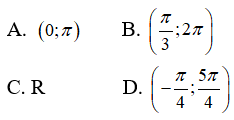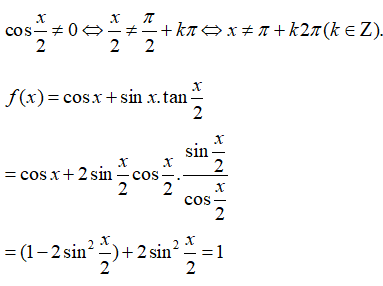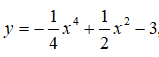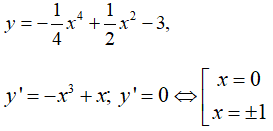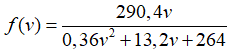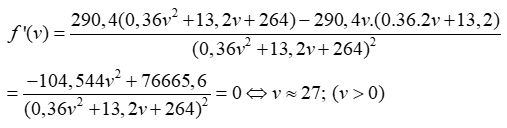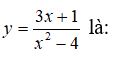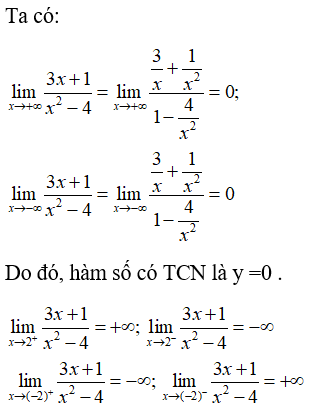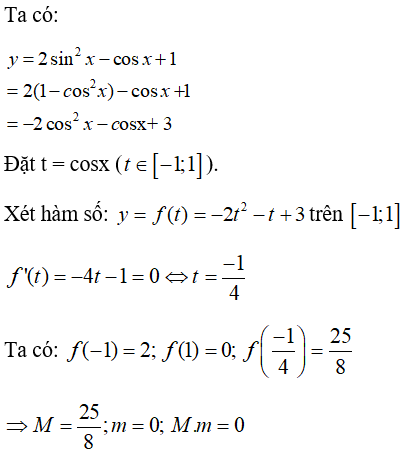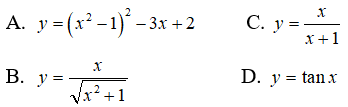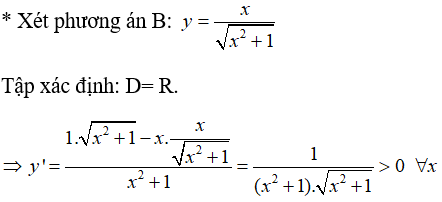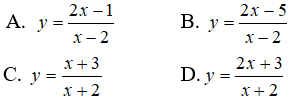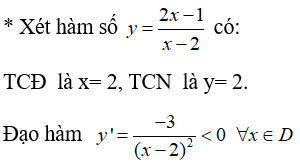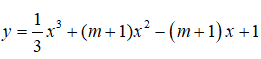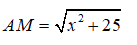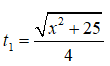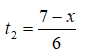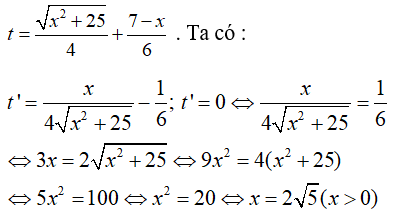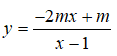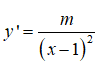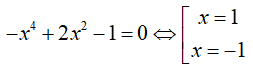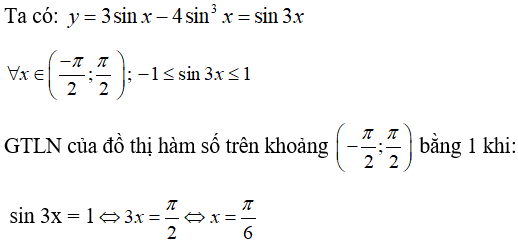Bài 1: Hàm số:

là hàm hằng trên khoảng nào sau đây?

Điều kiện:

Hàm số là hàm hằng x ≠ π +2kπ (k ∈ Z)

Do đó, hàm số đã cho cũng là hàm hằng trên khoảng (0; π) .

Bài 2: Trong các khẳng định sau về hàm số

khẳng định nào là đúng?

A. Hàm số có điểm cực tiểu là x = 0

B. Hàm số có hai điểm cực đại là x = ±1

C. Cả A và B đều đúng;

D. Cả A và B đều sai,

Lập bảng biến thiên, ta thấy hàm số có điểm cực tiểu là x = 0, có hai điểm cực đại là x = 1 và x = -1.

Bài 3: Trong các mệnh đề sau, hãy tìm mệnh đề sai:

A. Hàm số y = -x³ + 3x² - 3 có cực đại và cực tiểu;

B. Hàm số y = x³ + 3x + 1 có cực trị;

C. Hàm số 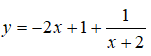 không có cực trị;

D. Hàm số 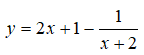 đồng biến trên từng khoảng xác định.

Xét hàm số y=x³ + 3x + 1 có: y' = 3x² + 3

Phương trình y’ = 0 vô nghiệm. Do đó, hàm số này không có cực trị

⇔ mệnh đề B sai .

Bài 4: Lưu lượng xe vào hầm cho bởi công thức

trong đó v (km/h) là vận tốc trung bình của các xe khi vào hầm. Với giá trị xấp xỉ nào của v thì lưu lượng xe là lớn nhất?

A. 26    

B.27    

C. 28    

D. 29

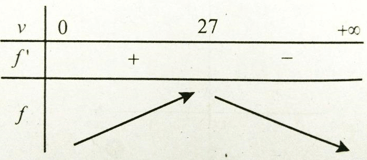
Xét

Hàm số đạt giá trị lớn nhất tại v ≈ 27 .

Bài 5: Đồ thị hàm số nào sau đây có hình dạng như hình bên?

A. y = x³ + 3x + 1

B. y = x³ - 3x + 1

C. y = -x³ - 3x + 1

D. y = - x³ + 3x + 1

Dựa vào hình vẽ ta suy ra, hàm số đã cho là hàm số bậc ba có hệ số a > 0 và hàm số không có điểm cực trị.

⇒ Loại C và D.

* Xét phương án A y = x³ + 3x + 1

có y' = 3x² + 3 nên hàm số không có cực trị.

⇒ A thỏa mãn

* xét phương án B: y = x³ - 3x + 1 có y' = 3x² - 3; y' = 0 ⇔ x = ±1

Và y’ đổi dấu khi qua 2 điểm 1; -1 . Do đó, hàm số này có 2 điểm cực trị.

⇒ Loại B

Bài 6: Số đường tiệm cận của đồ thị hàm số

A. 3    

B.2    

C. 1   

D.4

Suy ra, hàm số có tiệm cận đứng x = ±2.

Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.

Bài 7: Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2sin²x - cosx + 1 thì M.m bằng

A. 0    

B. 25/8    

C. 25/4    

D. 2

Bài 8: Hàm số nào sau đây là hàm số đồng biến trên R

* Xét phương án A: y = (x² - 1)² - 3x + 2

y'=2(x²-1).2x - 3 = 4x³ - 4x - 3

Và y’ > 0 không đúng với ∀ x ∈ R

Do đó, hàm số này đồng biến trên R.

Chọn B.

* Phương án C và D, hàm số có tập xác định không phải là R nên hàm số không thể đồng biến trên R.

Bài 9: Cho hàm số y = - x³ + 3x² - 3x + 1, mệnh đề nào sau đây là đúng?

A. Hàm số luôn nghịch biến.

B. Hàm số luôn đồng biến

C. Hàm số đạt cực đại tại x = 1

D. Hàm số đạt cực tiểu tại x = 1

y' = -3x² + 6x - 3 = -3(x² - 2x + 1) = -3(x - 1)² ≤ 0 ∀x ∈ R. Hàm số luôn nghịch biến.

Bài 10: Cho hàm số 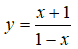 và các mệnh đề sau

(1) Hàm số trên nhận điểm I(1;-1) làm tâm đối xứng,

(2) Hàm số trên nhận đường thẳng y = -x làm trục đối xứng.

(3) Hàm số trên nhận y = -1 là tiệm cận đứng.

(4) Hàm số trên luôn đồng biến trên R .

Trong số các mệnh đề trên, số mệnh đề sai là

A. 1    

B.2    

C.3    

D. 4

+ Hàm số có tiệm cận đứng x=1 và tiệm cận ngang y= -1. Giao điểm của hai đường tiệm cận là I(1; -1) là tâm đối xứng của đồ thị. Mệnh đề 1 đúng, mệnh đề 3 sai.

+ Vì đường thẳng y=-x là một phân giác của góc tạo bởi 2 đường tiệm cận nên đường thẳng y=-x là một trục đối xứng của đồ thị hàm số. Mệnh đề 2 đúng.

+ Hàm số có tập xác định là R\{1}, nên hàm số không thể luôn đồng biến trên R.Mệnh đề 4 sai.

Bài 11: Cho hàm số y = x² - 2|x| + 2 và các mệnh đề

(1) Hàm số trên liên tục trên R

(2) Hàm số trên có đạo hàm tại x = 0

(3) Hàm số trên đạt GTNN tại x = 0.

(4) Hàm số trên đạt GTLN tại x = 0.

(5) Hàm số trên là hàm chẵn

(6) Hàm số trên cắt trục hoành tại duy nhất một điểm

Trong các mệnh đề trên, số mệnh đề đúng là

A.1   

B. 2    

C.3   

D. 4

* Hàm số đã cho liên tục trên R vì với 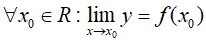 nên (1) đúng

* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.

*y = x² - 2|x| + 2 = |x|² - 2|x| + 2 = (|x| - 1)² + 1 ≥ 1 ∀ x

Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1

nên hàm số không có GTLN.

* Phương trình x² - 2|x| + 2=0 vô nghiệm nên đồ thị không cắt trục hoành.

f(-x)=(-x)² - 2|-x| + 2 = x² - 2|x| + 2 = f(x)

Nên hàm số đã cho là hàm số chẵn.

Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.

Bài 12: Cho hàm số y = -x² - 4x + 3 có đồ thị (C). Nếu tiếp tuyến tại M của (C) có hệ số góc bằng 8 thì hoành độ điểm M là:

A. 12    

B. -6    

C. -1   

D. 5

Đạo hàm y’ = -2x - 4 = 8

Hệ số góc tại điểm có hoành độ x₀ là: k = y'(x₀) = -2x₀ - 4

Để k = 8 thì -2x₀ - 4 = 8 ⇔ x₀ = -6

Vậy nếu tiếp tuyến tại M của (C) có hệ số góc bằng 8 thì hoành độ điểm M là -6.

Bài 13: Trong các tiếp tuyến tại các điểm trên đồ thị hàm số y = x³ - 3x² + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng:

A. -3   

B. 3   

C. -4   

D. 0

Tiếp tuyến của đồ thị hàm số có hệ số góc là

k = y' = 3x² - 6x = (3x² - 6x + 3) - 3 = 3(x - 1)² - 3 ≥ -3 ∀x ∈ R

Trong các tiếp tuyến tại các điểm trên đồ thị hàm số, tiếp tuyến có hệ số góc nhỏ nhất bằng -3.

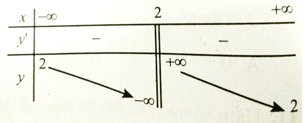
Bài 14: Hàm số nào sau đây có bảng biến thiên như hình bên?

* Đồ thị hàm số đã cho có TCĐ là x =2, TCN là y = 2.

Hàm số nghịch biến trên TXĐ.

Chọn A.

Bài 15: Hàm số y = x³ - 3x² + mx đạt cực tiểu tại x = 2 khi:

A.m < 0   

B. m > 0   

C. m = 0    

D. m ≠ 0

Hàm số y = x³ - 3x² + mx đạt cực tiểu tại x = 2 khi và chỉ khi:

Bài 16: Hàm số

đồng biến trên tập xác định của nó khi:

A. -2 ≤ m ≤ -1    

B. -2 < m < -1   

C. m < -2   

D. m > -1

àm số 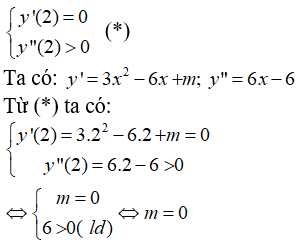 có tập xác định: D = R.

y'=x² + 2(m + 1)x - m - 1

Để hàm số đã cho đồng biến trên R khi và chỉ khi:

y' = f(x) = x² + 2(m + 1)x - m - 1 ≥ 0 ∀ x ∈ R

⇔ Δ' = (^m + m + 1 = m² + 3m + 2 ≤ 0

⇔ -2 ≤ m ≤ -1

Bài 17: Cho đồ thị hàm số y = x³ - 2x² + 2x (C). Gọi x₁,x₂ là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2017 . Khi đó (x₁, x₂) bằng

A. 4   

B. -4/3    

C. 4/3    

D. -1

Tiếp tuyến của C vuông góc với đường thẳng y= -x + 2017 nên hệ số góc của tiếp tuyến là k₂ thỏa mãn (-1)k₂ = -1 => k₂ = 1

Suy ra k₂ = y' = 1 => 3x² - 4x + 2 <=> 3x² - 4x + 2 = 0 (*)

Vì x₁, x₂ là nghiệm của (*) nên áp dụng Vi-ét ta có x₁ + x₂ = 4/3

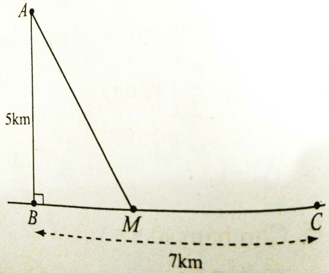
Bài 18: Một ngọn hải đăng đặt trại vị trí A cách bờbiển một khoảng AB = 5km. Trên bờ biển có một kho vị trí C cách B một khoảng là 7km. Do địa hình hiểm trở, người canh hải đăng chỉ có thể chèo thuyền từ A đến M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C, với vận tốc 6km/h. Vậy vị trí M cách B một khoảng bao xa thì người đó đến kho là nhanh nhất?

A. 3,5km   

B. 4,5km   

C. 5,5km   

D. 6,5km

Đặt BM = x (0 ≤ x ≤ 7) => MC = 7 - x. Áp dụng định lí Py-ta-go cho tam giác vuông ABM có

Thời gian đi từ A đến M là

thời gian đi từ M đến C là

Tổng thời gian đi từ A đến C là

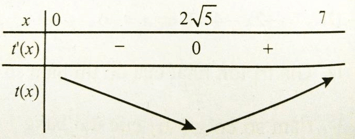
Bảng biến thiên

Để người đó đến kho nhanh nhất thì thời gian đi cần ít nhất, tức t đạt giá trị nhỏ nhất. Dựa vào bảng biến thiên ta thấy t đạt giá trị nhỏ nhất tại x = 2√5 ≈ 4,5

Vậy vị trí điểm M cách B một khoảng là 4,5km thì người đó đến kho là nhanh nhất.

Bài 20: Hàm số

đồng biến trên từng khoảng xác định của nó khi:

A. m > 0    

B. m < 0    

C. m ≠ 1    

D. m > 0

Để hàm số tăng trên từng khoảng xác định thì y’ > 0 <=> m > 0.

Bài 20: Cho hàm số y = -x⁴ + 2x² - 1. Số giao điểm của đồ thị hàm số với trục Ox là:

A. 1   

B.2   

C. 3    

D. 4

Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:

Số giao điểm của đồ thị hàm số với trục Ox là hai điểm.

Bài 21: Cho hàm số y = 3sinx - 4sin³x. Giá trị lớn nhất của hàm số trên khoảng (-π/2 ; π/2) bằng

A. -1    

B. π/6    

C. 1   

D. -π/6

Bài 22: Cho hàm số y = x³ - 3x² + 1. Tích các giá trị cực đại và giá trị cực tiểu của hàm số bằng

A. -6   

B. -3   

C.0    

D. 3

Ta có: y(0) = 1; y(2) = -3

Lập bảng biến thiên suy ra,Hàm số có giá trị cực đại bằng 1 và giá trị cực tiểu bằng -3. Tích của giá trị cực đại và giá trị cực tiểu bằng -3.

Bài 23: Số đường thẳng đi qua điểm A(0; 3) và tiếp xúc với đồ thị hàm số y = x⁴ - 2x² + 3 là:

A. 0   

B. 1   

C. 2   

D. 3

Ta có y' = 4x³ - 4x . Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x₀ có dạng

Ứng với ba giá trị của x ta viết được ba phương trình đường thẳng thỏa mãn đầu bài.

Vậy có 3 đường thẳng thỏa mãn yêu cầu bài toán.

Bài 24: Thể tích V của 1kg nước ở nhiệt độ T(0^o ≤ T ≤ 30^o) được cho bởi công thức V = 999,87 - 0,06426T + 0,0085043T² - 0,0000679T³. Ở nhiệt độ xấp xỉ bao nhiêu thì nước có khối lượng riêng lớn nhất?

A. 1   

B.2    

C. 3   

D. 4