Giải bài tập Toán 7 Bài 1: Các góc ở vị trí đặc biệt

Hoạt động khởi động

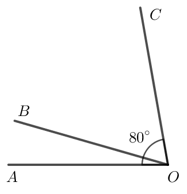
Khởi động trang 69 Toán lớp 7 Tập 1: Thế nào là hai góc kề nhau nhỉ?

Lời giải:

Sau bài học này chúng ta sẽ trả lời được câu hỏi trên như sau:

Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.

1. Hai góc kề bù

Khám phá 1 trang 69 Toán lớp 7 Tập 1: 

a) Quan sát Hình 1 và cho biết hai góc $\widehat{xOy}$ và $\widehat{yOz}$ có:

- Cạnh nào chung?

- Điểm trong nào chung?

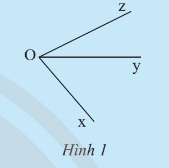
b) Hãy đo các góc $\widehat{xOy},\widehat{yOz},\widehat{xOz}$ trong Hình 1 rồi so sánh tổng số đo của $\widehat{xOy}$ và $\widehat{yOz}$ với $\widehat{xOz}$.

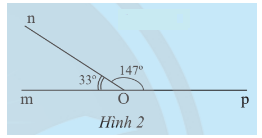
c) Tính tổng số đo của hai góc $\widehat{mOn}$ và $\widehat{nOp}$ trong Hình 2.

Lời giải:

a) Hai góc $\widehat{xOy}$ và $\widehat{yOz}$ có cạnh chung là Oy và không có điểm trong chung.

b) Sử dụng thước đo góc, ta đo được $\widehat{xOy}$ = 50°, $\widehat{y\text{O}z}$ = 26°, $\widehat{xOz}$ = 76°.

Khi đó $\widehat{xOy}+\widehat{y\text{O}z}=\widehat{xOz}$.

c) Tổng số đo hai góc $\widehat{mOn}$ và $\widehat{nOp}$ là: 33^o + 147^o = 180^o.

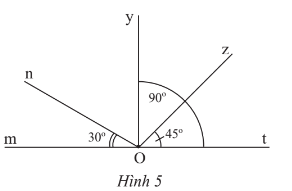
Thực hành 1 trang 69 Toán lớp 7 Tập 1: Quan sát Hình 5.

a) Tìm các góc kề với $\widehat{tOz}$.

b) Tìm số đo của góc kề bù với $\widehat{mOn}$.

c) Tìm số đo của $\widehat{nOy}$.

d) Tìm số đo của góc kề bù với $\widehat{tOz}$.

Lời giải:

a) Các góc kề với $\widehat{tOz}$ là: $\widehat{zOy},\widehat{zOn},\widehat{zOm}$.

b) Góc kề bù với $\widehat{mOn}$ là $\widehat{nOt}$.

Do $\widehat{nOt}$ là góc kề bù với $\widehat{mOn}$ nên $\widehat{mOn}+\widehat{nOt}=180°$.

Do đó $\widehat{nOt}=180°-\widehat{mOn}$ hay $\widehat{nOt}=180°-30°=150°$.

c) Do Oy nằm giữa Ot và On nên $\widehat{nOy}+\widehat{yOt}=\widehat{nOt}$

Do đó $\widehat{nOy}=\widehat{nOt}-\widehat{y\text{O}t}$ hay $\widehat{nOy}=150°-90°=60°$.

d) Góc kề bù với $\widehat{tOz}$ là $\widehat{zOm}$.

Do $\widehat{zOm}$ là góc kề bù với $\widehat{tOz}$ nên $\widehat{tOz}+\widehat{zOm}=180°$.

Do đó $\widehat{zOm}=180°-\widehat{tOz}$ hay $\widehat{zOm}=180°-45°=135°$.

Vận dụng 1 trang 70 Toán lớp 7 Tập 1: Hình 6 mô tả con dao và bàn cắt. Hãy tìm hai góc kề bù có trong hình.

Lời giải:

Hai góc kề bù có trong hình là $\widehat{xOy}$ và $\widehat{y\text{O}z}$.

2. Hai góc đối đỉnh

Khám phá 2 trang 70 Toán lớp 7 Tập 1: Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. Hãy cho biết quan hệ về cạnh, quan hệ về đỉnh của ${\widehat{O}}_1$ và ${\widehat{O}}_3$.

Lời giải:

Quan hệ về cạnh của ${\widehat{O}}_1$ và ${\widehat{O}}_3$: Ox là tia đối của Oy, Ot là tia đối của Oz.

Quan hệ về đỉnh của ${\widehat{O}}_1$ và ${\widehat{O}}_3$: Hai góc có chung đỉnh O.

Thực hành 2 trang 70 Toán lớp 7 Tập 1: 

a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ.

b) Vẽ $\widehat{xOy}$ rồi vẽ $\widehat{tOz}$ đối đỉnh với $\widehat{xOy}$.

c) Cặp góc $\widehat{xDy}$ và $\widehat{zDt}$ trong Hình 8a và cặp góc $\widehat{xMz}$ và $\widehat{tMy}$ trong Hình 8b có phải là các cặp góc đối đỉnh hay không? Hãy giải thích tại sao.

Lời giải:

a)

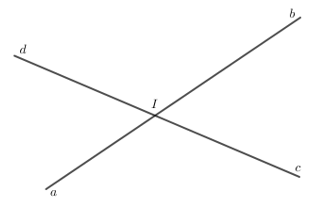
Các cặp góc đối đỉnh: $\widehat{aI\text{d}}$ và $\widehat{cIb}$; $\widehat{bI\text{d}}$ và $\widehat{cIa}$.

b) Thực hiện theo các bước như sau:

Bước 1. Vẽ góc xOy bất kì.

Bước 2. Vẽ Ot là tia đối của Ox, Oz là tia đối của Oy. Ta thu được góc tOz cần vẽ.

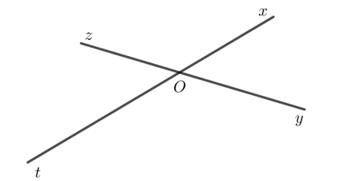
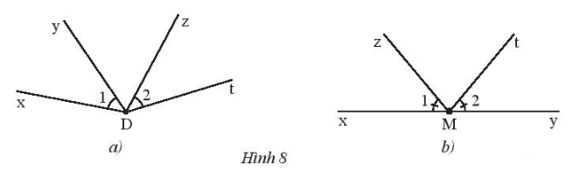
c) - Hai góc $\widehat{xDy}$ và $\widehat{zDt}$ trong Hình 8a không phải hai góc đối đỉnh do mỗi cạnh của $\widehat{xDy}$ không phải tia đối của một cạnh của $\widehat{zDt}$.

- Hai góc $\widehat{xMz}$ và $\widehat{tMy}$ trong Hình 8b không phải hai góc đối đỉnh do Oz không phải tia đối của Ot.

Vận dụng 2 trang 70 Toán lớp 7 Tập 1: Hai chân chống AB và CD của cái bàn xếp ở Hình 9 cho ta hình ảnh hai đường thẳng cắt nhau tại điểm O. Hãy chỉ ra các góc đối đỉnh trong hình.

Lời giải:

Các cặp góc đối đỉnh là: $\widehat{AO\text{D}}$ và $\widehat{COB}$, $\widehat{BO\text{D}}$ và $\widehat{COA}$.

3. Tính chất của hai góc đối đỉnh

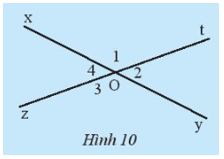
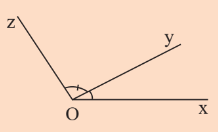
Khám phá 3 trang 71 Toán lớp 7 Tập 1: Quan sát Hình 10.

a) Hãy dùng thước đo góc để đo ${\widehat{O}}_1$ và ${\widehat{O}}_3$. So sánh số đo hai góc đó.

b) Hãy dùng thước đo góc để đo ${\widehat{O}}_2$ và ${\widehat{O}}_4$. So sánh số đo hai góc đó.

Lời giải:

a) Sử dụng thước đo góc ta đo được ${\widehat{O}}_1$ = 133^o; ${\widehat{O}}_3$ = 133^o.

Ta có ${\widehat{O}}_1$ = ${\widehat{O}}_3$.

b) Sử dụng thước đo góc ta đo được ${\widehat{O}}_2$ = 47^o; ${\widehat{O}}_4$ = 47^o.

Ta có ${\widehat{O}}_2$ =${\widehat{O}}_4$.

Thực hành 3 trang 71 Toán lớp 7 Tập 1: Quan sát Hình 12.

a) Tìm góc đối đỉnh của $\widehat{yOv}$.

b) Tính số đo của $\widehat{uOz}$.

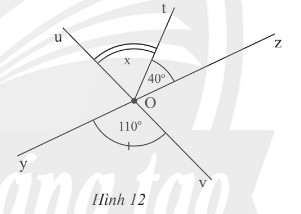
Lời giải:

a) Góc đối đỉnh của $\widehat{yOv}$ là $\widehat{uOz}$.

b) Do $\widehat{uOz}$ là góc đối đỉnh của $\widehat{yOv}$ nên $\widehat{uOz}=\widehat{y\text{Ov}}$.

Do đó $\widehat{uOz}$ = 110^o.

Vận dụng 3 trang 71 Toán lớp 7 Tập 1: Tìm số đo x của $\widehat{uOt}$ trong Hình 12.

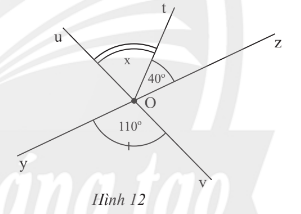
Lời giải:

Ta có: $\widehat{uOz}={110}^o$.

Do Ot nằm giữa Ou và Oz nên $\widehat{uOt}+\widehat{tOz}=\widehat{uOz}$

Do đó $\widehat{uOt}=\widehat{uOz}-\widehat{tOz}$ hay $\widehat{uOt}=110°-40°=70°.$

Vậy x = 70^o.

Bài tập

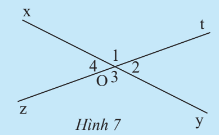
Bài 1 trang 72 Toán lớp 7 Tập 1: Quan sát Hình 14.

a) Tìm các góc kề với $\widehat{xOy}$.

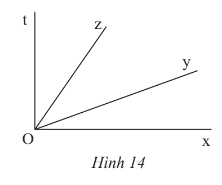
b) Tìm số đo của $\widehat{tOz}$ nếu cho biết $\widehat{xOy}={20}^o;\widehat{xOt}={90}^o;\widehat{yOz}=\widehat{tOz}$.

Lời giải:

a) Các góc kề với $\widehat{xOy}$ là: $\widehat{y\text{O}z},\widehat{y\text{O}t}$.

b) Do Oy nằm giữa Ox và Ot nên $\widehat{xOy}+\widehat{y\text{O}t}=\widehat{xOt}$.

Do đó $\widehat{y\text{O}t}=\widehat{xOt}-\widehat{xOy}$ hay $\widehat{y\text{O}t}=90°-20°=70°.$

Do Oz nằm giữa Oy và Ot nên $\widehat{y\text{O}z}+\widehat{tOz}=\widehat{y\text{O}t}$.

Mà $\widehat{y\text{O}z}=\widehat{tOz}$ nên $2\widehat{tOz}=\widehat{y\text{O}t}$.

Do đó $\widehat{tOz}=\frac{\widehat{y\text{O}t}}{2}=\frac{70°}{2}$= 35^o.

Vậy $\widehat{tOz}$ = 35^o.

Bài 2 trang 72 Toán lớp 7 Tập 1: Cho hai góc $\widehat{xOy},\widehat{yOz}$ kề bù với nhau. Biết $\widehat{xOy}={25}^o$. Tính $\widehat{yOz}$.

Lời giải:

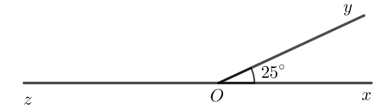
Do $\widehat{xOy}$ và $\widehat{y\text{O}z}$ là hai góc kề bù nên $\widehat{xOy}+\widehat{y\text{O}z}=180°.$

Do đó $\widehat{y\text{O}z}=180°-\widehat{xOy}$ = 180^o - 25^o = 155^o.

Vậy $\widehat{y\text{O}z}$ = 155^o.

Bài 3 trang 72 Toán lớp 7 Tập 1: Cho hai góc kề nhau $\widehat{AOB}$ và $\widehat{BOC}$ với $\widehat{AOC}={80}^o$. Biết $\widehat{AOB}=\frac{1}{5}\widehat{AOC}$. Tính số đo các góc $\widehat{AOB}$và $\widehat{BOC}$.

Lời giải:

Do $\widehat{AOB}=\frac{1}{5}\widehat{AOC}$ nên $\widehat{AOB}=\frac{1}{5}$.80^o = 16^o.

Do $\widehat{AOB}+\widehat{BOC}=\widehat{AOC}$ (do hai góc $\widehat{AOB}$ và $\widehat{BOC}$ kề nhau) nên $\widehat{BOC}=\widehat{AOC}-\widehat{AOB}$ = 80⁰ - 16^o = 64^o.

Vậy $\widehat{AOB}$ = 16^o, $\widehat{BOC}$ = 64^o.

Bài 4 trang 72 Toán lớp 7 Tập 1: Tìm số đo các góc còn lại trong mỗi hình sau.

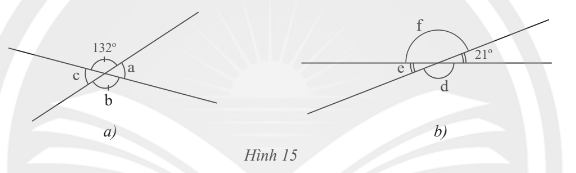
Lời giải:

+) Xét Hình 15a:

b là góc đối đỉnh với góc 132^o nên b = 132^o.

a là góc kề bù với góc 132^o nên a + 132^o = 180^o.

Do đó a = 180^o - 132^o = 48^o.

c = a do 2 góc này đối đỉnh.

Do đó c = 48^o.

Vậy a = c = 48^o, b = 132^o.

+) Xét Hình 15b:

e là góc đối đỉnh với góc 21^o nên e = 21^o.

d là góc kề bù với góc 21^o nên d + 21^o = 180^o.

Do đó d = 180^o - 21^o = 159^o.

f = d do 2 góc này đối đỉnh.

Do đó f = 159^o.

Vậy d = f = 159^o, e = 21^o.

Bài 5 trang 72 Toán lớp 7 Tập 1: Cặp cạnh nào của các ô cửa sổ (Hình 16) vuông góc với nhau? Hãy dùng kí hiệu $(\perp )$ để biểu diễn chúng.

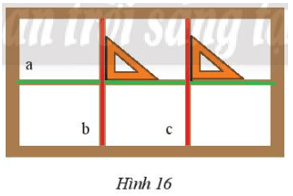
Lời giải:

Ta thấy a vuông góc với b, kí hiệu: $a\perp b$.

a vuông góc với c, kí hiệu: $a\perp c$.