Giải bài tập Toán 7 Bài tập cuối chương 4

Bài tập

Bài 1 trang 86 Toán lớp 7 Tập 1: Trong những câu sau, em hãy chọn những câu đúng.

Tia Oz là tia phân giác của góc $\widehat{xOy}$ khi:

a) $\widehat{xOz}=\widehat{yOz}$.

b) $\widehat{xOz}+\widehat{zOy}=\widehat{xOy}$.

c) $\widehat{xOz}=\widehat{yOz}=\frac{\widehat{xOy}}{2}$.

Lời giải:

a)

Gọi Ot là tia phân giác của $\widehat{xOy}$, khi đó $\widehat{y\text{O}t}=\widehat{xOt}$.

$\widehat{y\text{O}z}$ và $\widehat{y\text{O}t}$ là hai góc kề bù nên $\widehat{y\text{O}z}+\widehat{y\text{O}t}=180°$ do đó $\widehat{y\text{O}z}=180°-\widehat{y\text{O}t}$.

$\widehat{\text{xO}z}$ và $\widehat{\text{xO}t}$ là hai góc kề bù nên $\widehat{\text{xO}z}+\widehat{\text{xO}t}=180°$ do đó $\widehat{\text{xO}z}=180°-\widehat{\text{xO}t}$.

Mà $\widehat{y\text{O}t}=\widehat{xOt}$ nên $\widehat{y\text{O}z}=\widehat{xOz}$.

Ta thấy trong trường hợp này Oz không phải phân giác của $\widehat{xOy}$.

Do đó câu a sai.

b) Nếu $\widehat{xOz}+\widehat{zOy}=\widehat{xOy}$ thì Oz nằm giữa Ox và Oy, không đảm bảo Oz là tia phân giác của $\widehat{xOy}$.

Do đó câu b sai.

c) $\widehat{xOz}=\widehat{yOz}=\frac{\widehat{xOy}}{2}$ thì Oz nằm giữa Ox và Oy.

Lại có $\widehat{xOz}=\widehat{yOz}=\frac{\widehat{xOy}}{2}$ nên Oz là tia phân giác của $\widehat{xOy}$.

Do đó câu c đúng.

Bài 2 trang 86 Toán lớp 7 Tập 1: Quan sát Hình 1, biết d // h. Hãy kể tên một số cặp góc bằng nhau có trong Hình 1.

Lời giải:

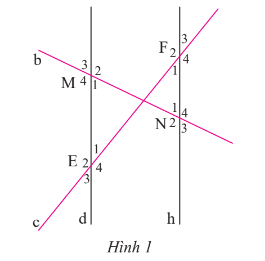
Quan sát Hình 1 ta thấy các cặp góc đối đỉnh bằng nhau.

Chẳng hạn: ${\widehat{M}}_2$ và ${\widehat{M}}_4$; ${\widehat{F}}_1$ và ${\widehat{F}}_3$; …

Do d // h nên ta có các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.

Chẳng hạn: ${\widehat{M}}_2$ và ${\widehat{N}}_2$ (so le trong); ${\widehat{E}}_3$ và ${\widehat{F}}_1$ (đồng vị); …

Bài 3 trang 87 Toán lớp 7 Tập 1: Quan sát Hình 2.

Chứng minh rằng xy // zt.

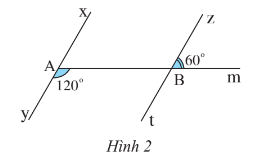
Lời giải:

Ta có $\widehat{tBm}$ và $\widehat{mB\text{z}}$ là hai góc kề bù nên $\widehat{tBm}+\widehat{mB\text{z}}=180°$.

Suy ra Do đó $\widehat{tBm}=180°-\widehat{mB\text{z}}$ = 180^o - 60^o = 120^o.

Do đó $\widehat{y\text{A}B}=\widehat{tBm}=120°$.

Mà hai góc này ở vị trí đồng vị nên Ay // Bt hay xy // zt.

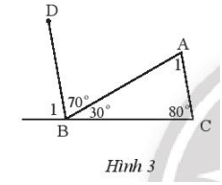
Bài 4 trang 87 Toán lớp 7 Tập 1: Quan sát Hình 3.

a) Tính ${\widehat{B}}_1$.

b) Chứng minh rằng AC // BD.

c) Tính ${\widehat{A}}_1$.

Lời giải:

a) Ta có ${\widehat{B}}_1$ + 70° + 30° = 180° nên ${\widehat{B}}_1$ = 180° - 70° - 30° = 80°.

b) Do ${\widehat{B}}_1$ = 80° và $\widehat{ACB}=80°$ nên ${\widehat{B}}_1=\widehat{ACB}$ (cùng bằng 80°).

Mà hai góc này ở vị trí đồng vị nên AC // BD.

c) Do AC // BD nên ${\widehat{A}}_1=\widehat{AB\text{D}}$ (2 góc so le trong).

Do đó ${\widehat{A}}_1$ = 70^o.

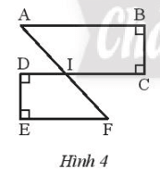
Bài 5 trang 87 Toán lớp 7 Tập 1: Quan sát Hình 4. Chứng minh rằng:

a) AB // CD và EF // CD.

b) AB // EF.

Lời giải:

a) Vì AB vuông góc với CB; CD vuông góc với BC nên AB // CD.

Vì EF vuông góc với DE; CD vuông góc với DE nên EF // CD.

b) Do AB // CD và EF // CD nên AB // EF.

Bài 6 trang 87 Toán lớp 7 Tập 1: Cho Hình 5 có ${\widehat{B}}_1={130}^o$. Số đo của ${\widehat{A}}_1$ là bao nhiêu?

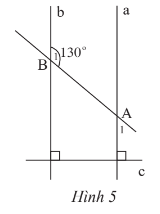
Lời giải:

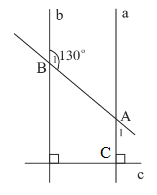
Do a và b cùng vuông góc với c nên a // b.

Do a // b nên ${\widehat{B}}_1=\widehat{BAC}$ (2 góc so le trong).

Do đó $\widehat{BAC}$ = 130^o.

$\widehat{BAC}$ và ${\widehat{A}}_1$ là hai góc kề bù nên $\widehat{BAC}+{\widehat{A}}_1=180°$.

Do đó ${\widehat{A}}_1=180°-\widehat{BAC}$ = 180^o - 130^o = 50^o.

Vậy ${\widehat{A}}_1$ = 50^o.

Bài 7 trang 87 Toán lớp 7 Tập 1: Cho Hình 6, biết hai đường thẳng a và b song song với nhau và ${\widehat{A}}_1={50}^o$.

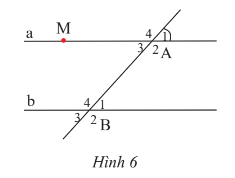
a) Hãy viết tên các cặp góc so le trong và các cặp góc đồng vị.

b) Tính số đo của ${\widehat{A}}_3,{\widehat{B}}_3$.

c) Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng minh rằng c ⊥ b.

Lời giải:

a) Các cặp góc so le trong: ${\widehat{A}}_2$ và ${\widehat{B}}_4$; ${\widehat{A}}_3$ và ${\widehat{B}}_1$.

Các cặp góc đồng vị: ${\widehat{A}}_1$ và ${\widehat{B}}_1$; ${\widehat{A}}_2$ và ${\widehat{B}}_2$; ${\widehat{A}}_3$ và ${\widehat{B}}_3$; ${\widehat{A}}_4$ và ${\widehat{B}}_4$.

b) ${\widehat{A}}_3$ và ${\widehat{A}}_1$ là hai góc đối đỉnh nên ${\widehat{A}}_3={\widehat{A}}_1$.

Do đó ${\widehat{A}}_3$ = 50^o.

Do a // b nên ${\widehat{A}}_3={\widehat{B}}_3$ (2 góc đồng vị).

Do đó ${\widehat{B}}_3$ = 50^o.

Vậy ${\widehat{A}}_3={\widehat{B}}_3$ = 50^o.

c)

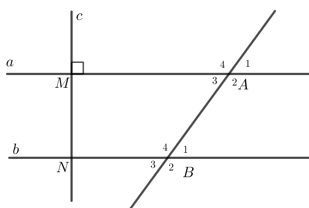
Ta có a // b và a ⊥ c

Suy ra c ⊥ b (một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại).

Vậy c ⊥ b.

Bài 8 trang 87 Toán lớp 7 Tập 1: Vẽ đường thẳng m song song với đường thẳng n. Vẽ đường thẳng d cắt đường thẳng m tại điểm I.

a) Hỏi nếu d // n thì điều này có trái với tiên đề Euclid không?

b) Sử dụng kết quả của câu a để chứng minh d cắt n.

Lời giải:

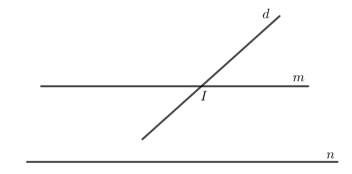
a) Ta có đường thẳng m đi qua I và song song với n.

Nếu đường thẳng d đi qua I cũng song song với n thì điều này mâu thuẫn với tiên đề Euclid.

b) Do d // n mâu thuẫn với tiên đề Euclid nên d không song song với n.

Mặt khác I thuộc d và I không thuộc n nên n và d không trùng nhau.

Do đó,  d cắt n.

Bài 9 trang 87 Toán lớp 7 Tập 1: Qua điểm O là chốt xoay của một cái kéo, kẻ hai đường thẳng xOy và zOt lần lượt song song với hai lưỡi kéo (Hình 7). Tìm các góc kề bù và các góc đối đỉnh có trong hình vừa vẽ.

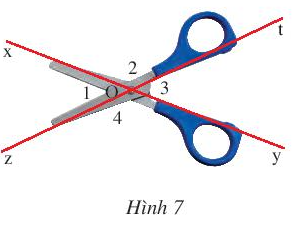
Lời giải:

Các cặp góc kề bù: $\widehat{xOz}$ và $\widehat{xOt}$; $\widehat{xOt}$ và $\widehat{tOy}$; $\widehat{tOy}$ và $\widehat{y\text{O}z}$; $\widehat{y\text{O}z}$ và $\widehat{xOz}$.

Các cặp góc đối đỉnh: $\widehat{xOz}$ và $\widehat{tOy}$; $\widehat{xOt}$ và $\widehat{y\text{O}z}$.