Giải bài tập Toán 7 Bài tập cuối chương 3

Bài tập

Bài 1 trang 66 Toán lớp 7 Tập 1: Một hình khối gồm 14 hình lập phương gắn kết với nhau như Hình 1. Mỗi hình lập phương có cạnh 1 cm. Hãy tính thể tích của hình khối này.

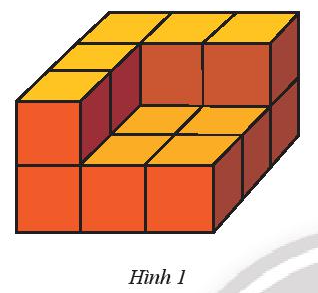
Lời giải:

Thể tích của một hình lập phương là: 1³ = 1 (cm³).

Thể tích của khối hình là: 14 . 1 = 14 (cm³).

Vậy thể tích của khối hình là 14 cm³.

Bài 2 trang 66 Toán lớp 7 Tập 1: Một bể cá hình hộp chữ nhật với kích thước mặt đáy là 5 dm và 12 dm, có mực nước là 7 dm. Người ta đổ vào đó một lượng cát (có độ thấm nước không đáng kể) thì thấy mực nước dâng thêm 1,5 dm và ngập cát đổ vào. Tính thể tích của lượng cát.

Lời giải:

Mực nước sau khi cho cát vào là 7 + 1,5 = 8,5 (dm).

Thể tích của bể cá khi chưa cho cát là: 5 . 12 . 7 = 420 (dm³).

Thể tích của bể cá khi cho cát là: 5 . 12 . 8,5 = 510 (dm³).

Thể tích của lượng cát là: 510 - 420 = 90 (dm³).

Vậy thể tích cát cho vào bể là 90 dm³.

Bài 3 trang 66 Toán lớp 7 Tập 1: Một khuôn đúc bê tông có kích thước như Hình 2. Bể dày các mặt bên của khuôn là 1,2 cm. Bề dày mặt đáy của khuôn là 1,9 cm. Thể tích của khối bê tông được khuôn này đúc ra là bao nhiêu xăngtimét khối?

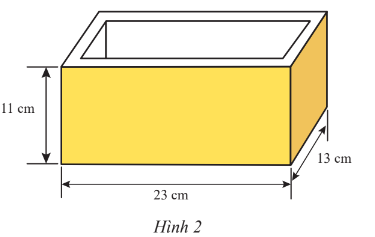
Lời giải:

Do bề dày các mặt bên của khuôn là 1,2 cm nên chiều rộng của mặt đáy khối bê tông được đúc ra là 13 - 1,2 - 1,2 = 10,6 (cm); chiều dài của mặt đáy khối bê tông được đúc ra là 23 - 1,2 - 1,2 = 20,6 (cm).

Do bề dày mặt đáy của khuôn là 1,9 cm nên chiều cao của khối bê tông được đúc ra là

11 - 1,9 = 9,1 (cm).

Thể tích của khối bê tông là:

10,6 . 20,6 . 9,1 = 218,36 . 9,1 = 1987,076 (cm³).

Vậy thể tích của khối bê tông là 1987,076 cm³.

Bài 4 trang 66 Toán lớp 7 Tập 1: Phần bên trong của một cái khuôn làm bánh có dạng hình hộp chữ nhật với đáy là hình vuông cạnh 20 cm, chiều cao 5 cm (Hình 3). Người ta dự định sơn phần bên trong bằng loại sơn không dính. Hỏi với một lượng sơn đủ bao phủ được 100 m² thì sơn được bao nhiêu cái khuôn làm bánh?

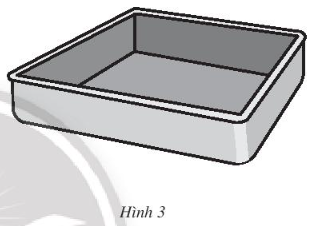
Lời giải:

Diện tích xung quanh của khuôn là: 2 . (20 + 20) . 5 = 400 (cm²).

Diện tích đáy của khuôn là: 20² = 400 (cm²).

Diện tích sơn của một khuôn gồm diện tích xung quanh và diện tích đáy của khuôn.

Diện tích sơn của một khuôn là: 400 + 400 = 800 (cm²).

Đổi 800 cm² = 0,08 m².

Vậy với một lượng sơn đủ bao phủ được 100 m² thì sơn được 100 : 0,08 = 1250 cái khuôn.

Bài 5 trang 66 Toán lớp 7 Tập 1: Một ngôi nhà có kích thước như Hình 4.

a) Tính thể tích của ngôi nhà.

b) Biết rằng 1 l sơn bao phủ được 4 m² tường. Hỏi phải cần ít nhất bao nhiêu lít sơn để sơn phủ được tường mặt ngoài ngôi nhà (không sơn cửa)? Biết tổng diện tích các cửa là 9 m².

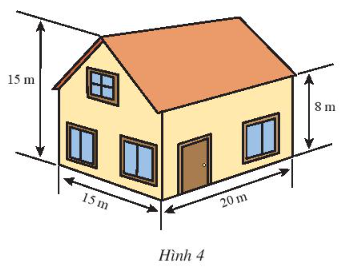
Lời giải:

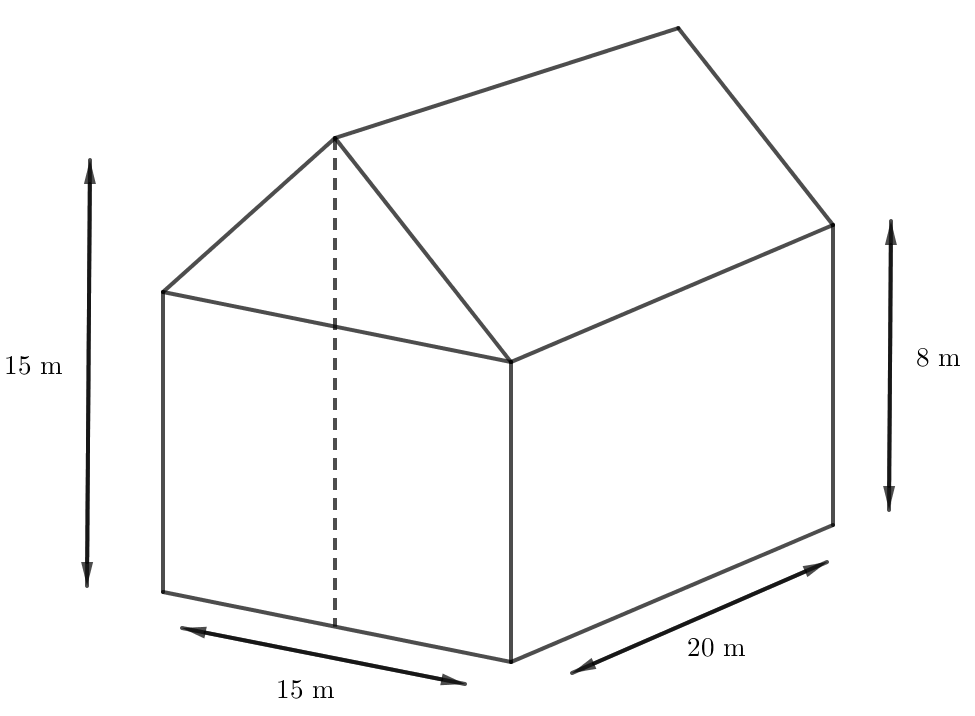
Ngôi nhà trên là hình lăng trụ đứng có đáy được chia thành hai hình thang có độ dài hai đáy lần lượt là 8 m và 15 m; chiều cao của hình thang là 15 : 2 = 7,5 m.

Do đó diện tích đáy bằng 2 lần diện tích hình thang vừa chia.

a) Diện tích hình thang là:

$\frac{\left(8+15\right).7,5}{2}$ = 86,25 (m²).

Diện tích mặt có ba cửa sổ của ngôi nhà là:

2 . 86,25 = 172,5 (m²).

Thể tích của ngôi nhà là: 172,5 . 20 = 3450 (m³).

 b) Diện tích mặt trước và mặt sau của ngôi nhà là:

2 . 20 . 8 = 320 (m²).

Tổng diện tích xung quanh của ngôi nhà là: 320 + 2 . 172,5 = 665 (m²).

Do tổng diện tích các cửa là 9 m² nên diện tích cần sơn là: 665 - 9 = 656 (m²).

Cần số lít sơn để phủ được hết mặt ngoài ngôi nhà là:

656 : 4 = 164 (l).

Vậy cần 164 l sơn để phủ được hết mặt ngoài ngôi nhà.

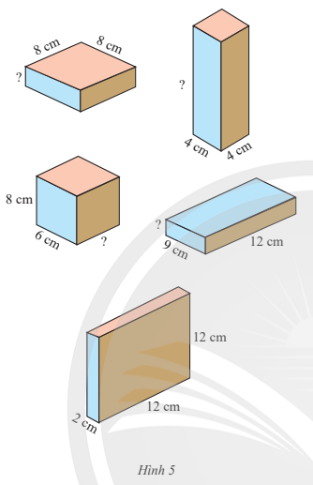
Bài 6 trang 67 Toán lớp 7 Tập 1: Các hình hộp chữ nhật trong Hình 5 có cùng số đo thể tích. Em hãy tìm các kích thước còn thiếu.

Lời giải:

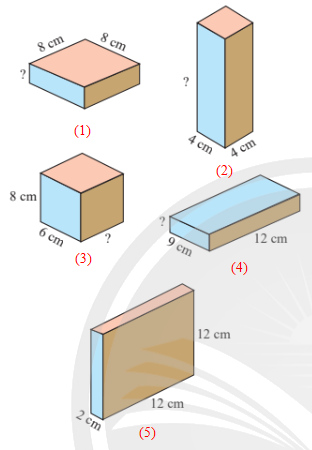
Thể tích của mỗi hình trong Hình 5 là:

2 . 12 . 12 = 288 (cm³).

Kích thước còn thiếu trong hình (1) là: 288 : 8 : 8 = 36 : 8 = 4,5 (cm).

Kích thước còn thiếu trong hình (2) là: 288 : 4 : 4 = 72 : 4 = 18 (cm).

Kích thước còn thiếu trong hình (3) là: 288 : 8 : 6 = 36 : 6 = 6 (cm).

Kích thước còn thiếu trong hình (4) là: 288 : 12 : 9 = 24 : 9 = $\frac{8}{3}$ (cm).

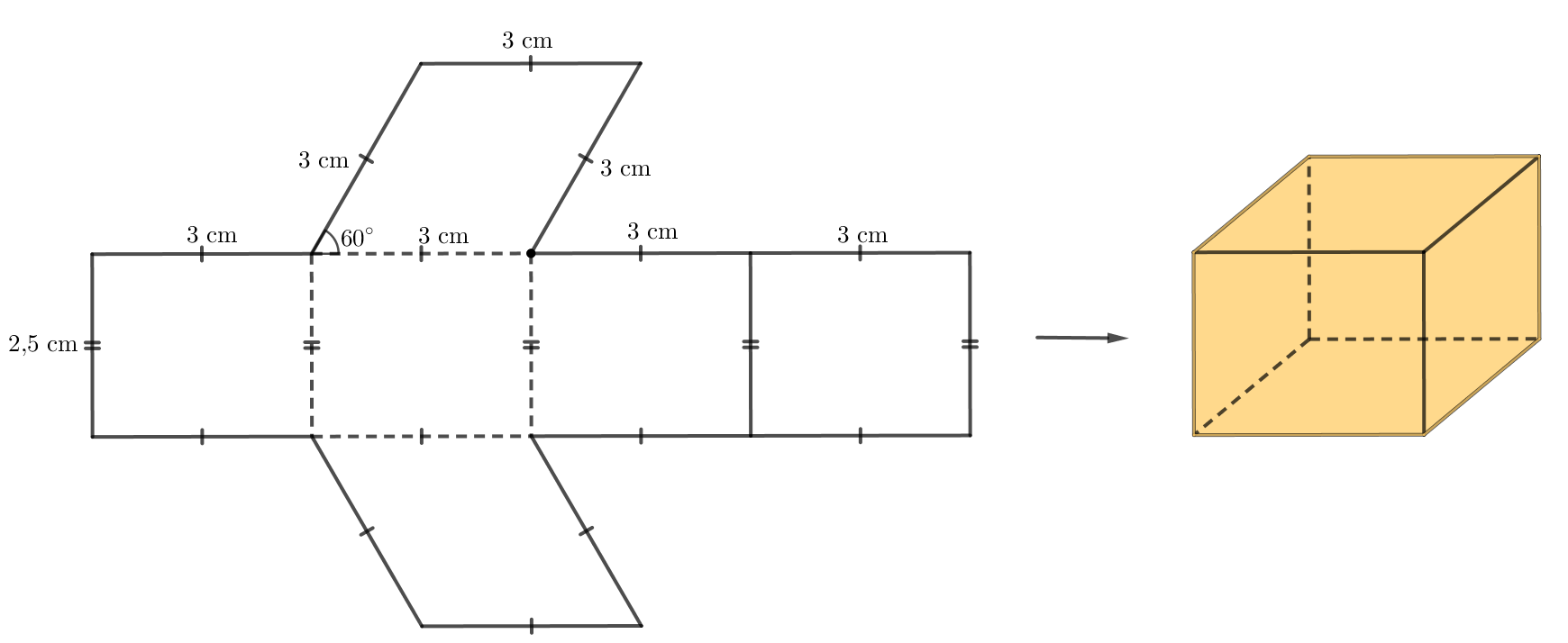
Bài 7 trang 67 Toán lớp 7 Tập 1: Tạo lập hình lăng trụ đứng có chiều cao 2,5 cm, đáy là hình thoi có cạnh 3 cm và một góc 60^o.

Lời giải:

Thực hiện tạo hình lăng trụ đứng như sau:

Bước 1. Vẽ một đoạn thẳng có độ dài 3 cm.

Bước 2. Tại một đầu mút của đoạn thẳng, vẽ đường tròn có bán kính bằng 3 cm và vẽ một đoạn thẳng sao cho đoạn thẳng đó tạo với đoạn thẳng ban đầu một góc 60^o.

- Trên một miếng bìa, vẽ bốn hình chữ nhật và hai hình thoi với kích thước như hình dưới.

- Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng hình thoi như hình dưới.

Bài 8 trang 67 Toán lớp 7 Tập 1: Hãy nêu các bước tạo lập hình lăng trụ đứng tam giác trong Hình 6.

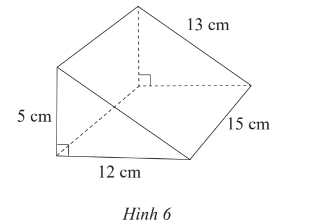
Lời giải:

Trên một miếng bìa, ta thực hiện tạo hình lăng trụ đứng như sau:

Bước 1. Vẽ đoạn thẳng có độ dài 13 cm.

Bước 2. Tại 2 điểm mút của đoạn thẳng, lần lượt vẽ hai đường tròn có bán kính 5 cm và 12 cm. Hai đường tròn này cắt nhau tại một điểm.

Nối điểm đó với hai đầu mút của đoạn thẳng, ta được tam giác vuông có độ dài 3 cạnh lần lượt là 5 cm; 12 cm và 13 cm.

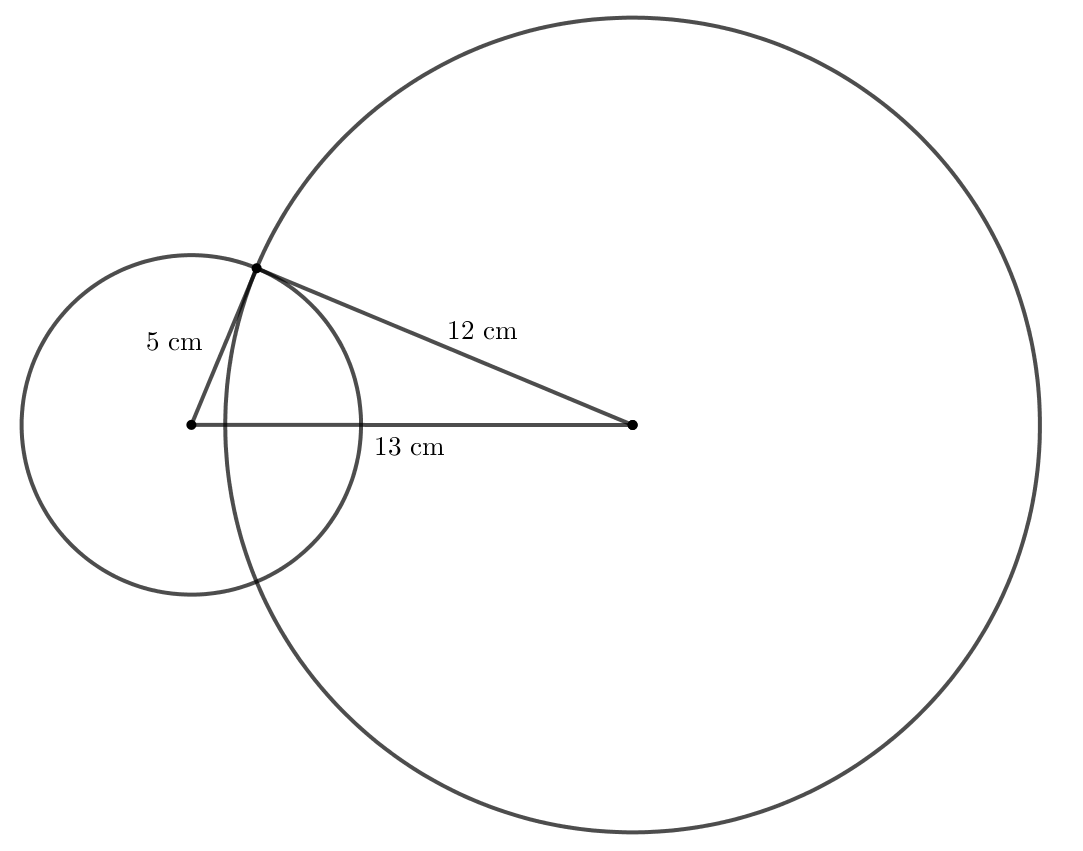
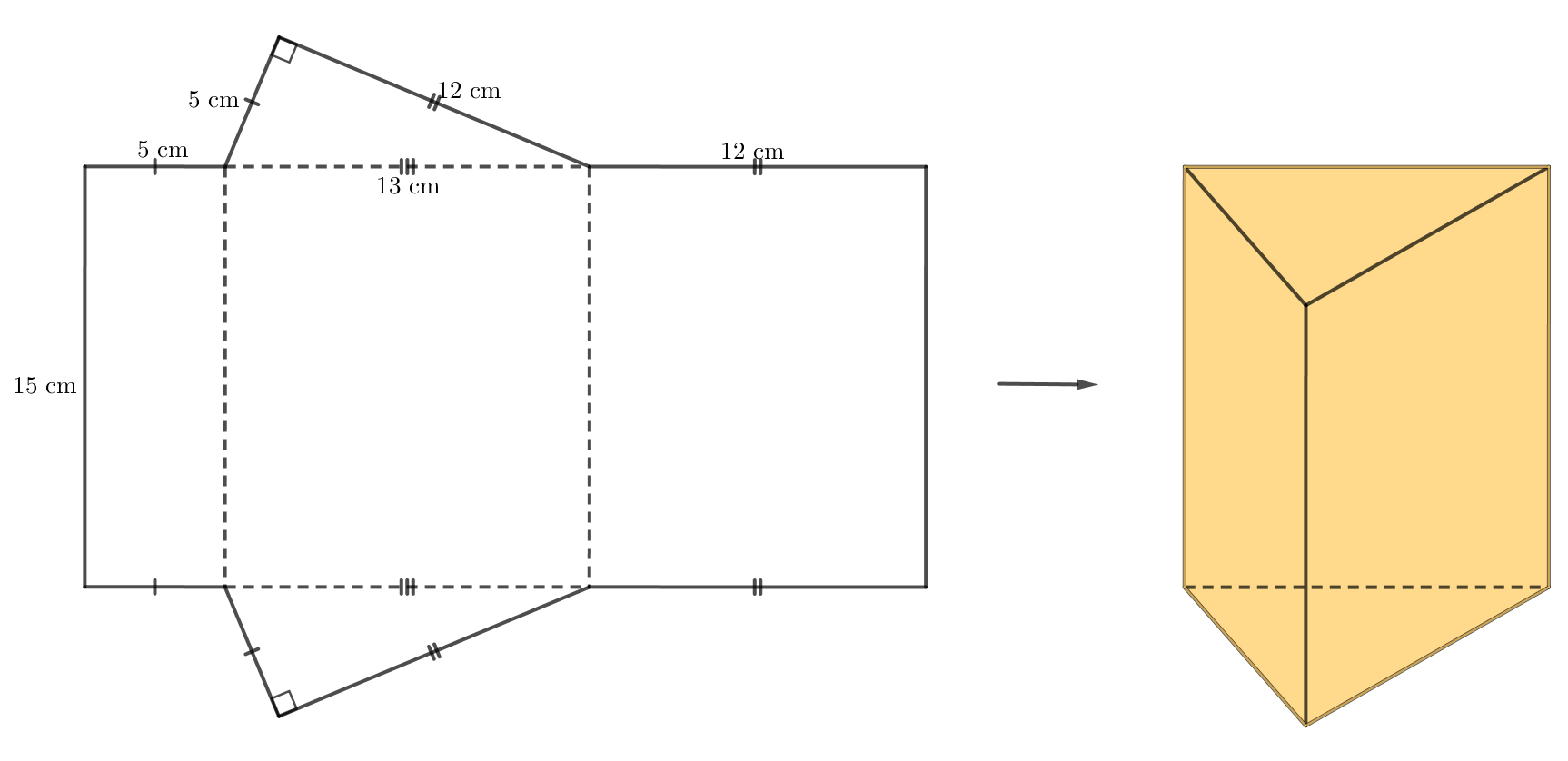
Bước 3. Sau đó thực hiện vẽ thêm ba hình chữ nhật và một tam giác vuông như hình dưới.

Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng tam giác vuông như hình dưới.

Bài 9 trang 67 Toán lớp 7 Tập 1: Người ta cắt một tấm bìa để tạo lập một lăng trụ đứng có đáy là tam giác đều với kích thước như Hình 7. Hãy cho biết độ dài các cạnh đáy và chiều cao của hình lăng trụ đứng đó.

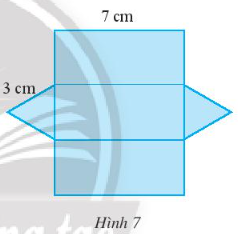
Lời giải:

Độ dài các cạnh đáy của hình lăng trụ là 3 cm.

Độ dài chiều cao của hình lăng trụ đứng là 7 cm.

Vậy hình lăng trụ đứng có đáy là tam giác đều có độ dài mỗi cạnh đáy đều bằng 3 cm và chiều cao là 7 cm.