Giải bài tập Toán 7 Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác 

Video giải bài tập Toán 7 Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác 

1. Diện tích xung quanh của hình lăng trụ đứng

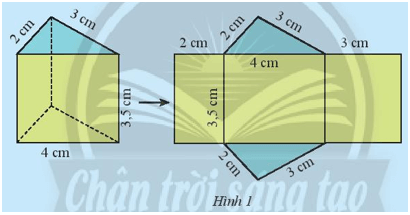
Khám phá 1 trang 59 Toán lớp 7 Tập 1: Hãy quan sát lăng trụ đứng tam giác (Hình 1) và thực hiện các yêu cầu sau:

a) Tính tổng diện tích ba mặt bên của hình lăng trụ đứng.

b) Gọi C_đáy là chu vi đáy và h là chiều cao của hình lăng trụ, tính C_đáy . h.

c) So sánh kết quả của câu a và câu b.

Lời giải:

a) Tổng diện tích ba mặt bên của hình lăng trụ đứng là:

4 . 3,5 + 3 . 3,5 + 2 . 3,5 = 14 + 10,5 + 7 = 31,5 (cm²).

b) Chu vi đáy là: 4 + 2 + 3 = 9 (cm).

Khi đó C_đáy . h = 9 . 3,5 = 31,5 (cm²).

c) Kết quả của câu a bằng kết quả của câu b.

Thực hành 1 trang 59 Toán lớp 7 Tập 1: Tính diện tích xung quanh của lăng trụ đứng có đáy là hình thang được cho trong Hình 2.

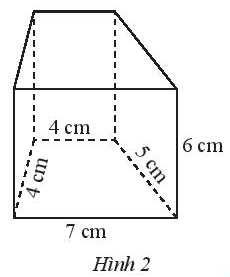
Lời giải:

Diện tích xung quanh của lăng trụ đứng trên là:

(4 + 4 + 5 + 7) . 6 = 20 . 6 = 120 (cm²).

Vậy diện tích xung quanh của lăng trụ trên là 120 cm².

2. Thể tích của hình lăng trụ đứng

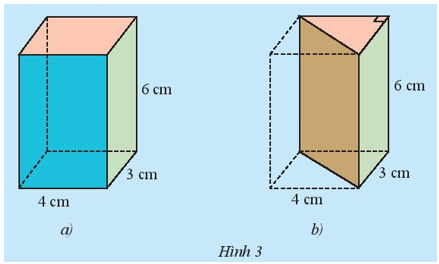
Khám phá 2 trang 60 Toán lớp 7 Tập 1: Cho hình hộp chữ nhật với kích thước như Hình 3a. Hình hộp này được cắt đi một nửa để có hình lăng trụ đứng như Hình 3b.

a) Tính thể tích của hình hộp chữ nhật.

b) Dự đoán thể tích của hình lăng trụ đứng tam giác dựa vào thể tích hình hộp chữ nhật ở câu a.

c) Gọi S_đáy là diện tích mặt đáy và h là chiều cao của hình lăng trụ đứng tam giác. Hãy tính S_đáy . h.

d) So sánh S_đáy . h và kết quả dự đoán ở câu b.

Lời giải:

a) Thể tích của hình hộp chữ nhật là: 4 . 3 . 6 = 72 (cm³).

b) Do hình hộp chữ nhật cắt đi một nửa để có hình lăng trụ đứng nên dự đoán thể tích hình lăng trụ bằng $\frac{1}{2}$ thể tích hình hộp chữ nhật.

Dự đoán thể tích hình lăng trụ đứng = $\frac{1}{2}.72$ = 36 (cm³).

c) Diện tích đáy của hình lăng trụ đứng tam giác là: $\frac{3.4}{2}$ = 6 (cm²).

Khi đó S_đáy . h = 6 . 6 = 36 (cm³).

d) Kết quả dự đoán ở câu b bằng S_đáy . h.

Thực hành 2 trang 60 Toán lớp 7 Tập 1: Tính diện tích xung quanh của một trụ bê tông hình lăng trụ đứng có chiều cao 2 m và đáy là tam giác đều có cạnh 0,5 m (Hình 4).

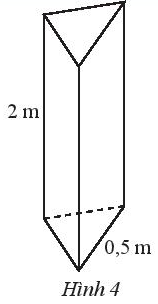
Lời giải:

Diện tích xung quanh của trụ bê tông có chiều cao 2 m và đáy là tam giác đều có cạnh 0,5 m là:

3. 0,5 . 2 = 3 (m²).

Vậy diện tích xung quanh của trụ bê tông đó là 3 m².

Thực hành 3 trang 60 Toán lớp 7 Tập 1: Tính thể tích lăng trụ đứng tứ giác có đáy là hình thang với kích thước cho trong Hình 5.

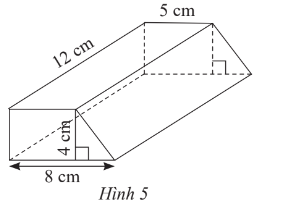
Lời giải:

Hình lăng trụ trên có đáy là hình thang với độ dài hai cạnh đáy lần lượt là 5 cm và 8 cm; số đo chiều cao là 4 cm.

Diện tích đáy của hình lăng trụ đó là:

$\frac{\left(5+8\right).4}{2}$ = 26 (cm²).
Thể tích của hình lăng trụ đó là:

26 . 12 = 312 (cm³).

Vậy thể tích của hình lăng trụ đứng đó là 312 cm³.

3. Diện tích xung quanh và thể tích của một số hình khối trong thực tiễn

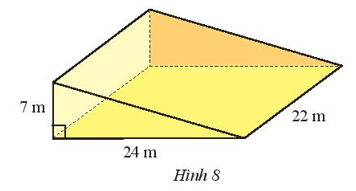
Thực hành 4 trang 61 Toán lớp 7 Tập 1: Để làm cầu bắc qua một con kênh, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như Hình 8. Hãy tính thể tích của một khối bê tông.

Lời giải:

Diện tích đáy của khối bê tông là:

$\frac{24.7}{2}$ = 84 (m²)

Thể tích của khối bê tông là:

84 . 22 = 1 848 (m³)

Vậy thể tích của khối bê tông đó là 1 848 m³.

Vận dụng trang 62 Toán lớp 7 Tập 1: Bạn Nam đã làm một chiếc hộp hình lăng trụ đứng với kích thước như Hình 9. Bạn ấy định sơn các mặt của chiếc hộp, trừ mặt bên dưới. Hãy tính diện tích cần sơn.

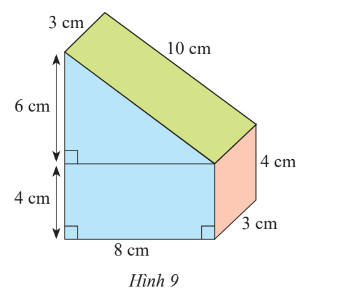
Lời giải:

Chiếc hộp hình lăng trụ đứng trên có đáy là hình thang với độ dài của hai cạnh đáy lần lượt là 4 cm và 4 + 6 = 10 (cm); chiều cao là 8 cm; độ dài của cạnh bên là 10 cm.

Chu vi đáy là: 4 + 10 + 8 + 10 = 32 (cm).

Diện tích xung quanh của chiếc hộp là: 32 . 3 = 96 (cm²)

Diện tích hai đáy của của chiếc hộp là: $2.\frac{\left(4+10\right).8}{2}$ = 112 (cm²).

Diện tích mặt bên dưới là: 8 . 3 = 24 (cm²).

Diện tích cần sơn bằng tổng diện tích xung quanh và diện tích hai đáy của chiếc hộp trừ đi diện tích mặt bên dưới.

Diện tích cần sơn là: 96 + 112 - 24 = 184 (cm²).

Vậy diện tích cần sơn là 184 cm².

Bài tập

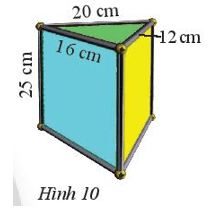
Bài 1 trang 62 Toán lớp 7 Tập 1: Một chiếc hộp đèn có dạng hình lăng trụ đứng tam giác có kích thước như Hình 10. Tính diện tích xung quanh của chiếc hộp.

Lời giải:

Chu vi đáy của chiếc hộp là: 20 + 16 + 12 = 48 (cm).

Diện tích xung quanh của chiếc hộp là: 48 . 25 = 1 200 (cm²).

Vậy diện tích xung quanh của chiếc hộp là 1 200 cm².

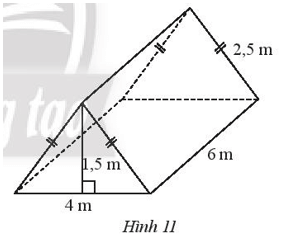
Bài 2 trang 62 Toán lớp 7 Tập 1: Một chiếc lều trại có hình dạng và kích thước như Hình 11. Tính tổng diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) và thể tích của chiếc lều.

Lời giải:

Chu vi đáy của chiếc lều là: 2,5 . 2 + 4 = 9 (m).

Diện tích xung quanh của chiếc lều là: 9 . 6 = 54 (m²).

Diện tích đáy của chiếc lều là: $\frac{4.1,5}{2}$ = 3 (m²).

Diện tích phần tiếp giáp với mặt đất là: 4 . 6 = 24 (m²).

Tổng diện tích tấm bạt có thể phủ kín bằng tổng diện tích xung quanh và diện tích hai đáy của chiếc lều trừ đi diện tích phần tiếp giáp với đất.

Khi đó tổng diện tích tấm bạt có thể phủ kín là: 54 + 2 . 3 - 24 = 36 (m²).

Thể tích của chiếc lều là: 3 . 6 = 18 m³.

Vậy diện tích tấm bạt có thể phủ là 36 m², thể tích của chiếc lều là 18 m³.

Bài 3 trang 62 Toán lớp 7 Tập 1: Một cái bục hình lăng trụ đứng có kích thước như Hình 12.

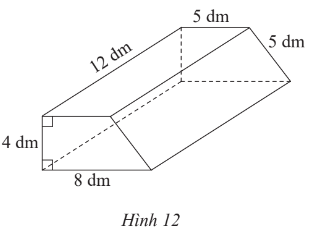
a) Người ta muốn sơn tất cả các mặt của cái bục. Diện tích cần phải sơn là bao nhiêu?

b) Tính thể tích của cái bục.

Lời giải:

a) Bục hình lăng trụ đứng có đáy là hình thang với độ dài hai cạnh đáy lần lượt là 5 dm và 8 dm; chiều cao là 4 dm; độ dài của cạnh bên là 5 dm.

Chu vi đáy của bục là: 4 + 5 + 5 + 8 = 22 (dm).

Diện tích đáy của bục là:

$\frac{\left(5+8\right).4}{2}$ = 26 (dm²).

Diện tích xung quanh của bục là: 22 . 12 = 264 (dm²).

Diện tích cần sơn bằng tổng diện tích xung quanh và diện tích hai đáy của bục nên diện tích cần sơn là: 264 + 2 . 26 = 316 (dm²).

Vậy diện tích cần sơn là 316 dm².

b) Thể tích của bục là:

26 . 12 = 312 (dm³).

Vậy thể tích của bục là 312 dm³.

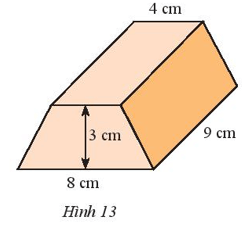
Bài 4 trang 63 Toán lớp 7 Tập 1: Tính thể tích hình lăng trụ đứng có đáy là hình thang cân với kích thước như Hình 13.

Lời giải:

Diện tích đáy của hình lăng trụ đó là:

$\frac{\left(4+8\right).3}{2}$ = 18 (cm²).

Thể tích của hình lăng trụ đó là:

18 . 9 = 162 (cm³).

Vậy thể tích của hình lăng trụ đó là 162 cm³.

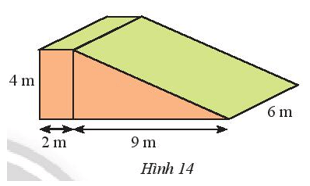
Bài 5 trang 63 Toán lớp 7 Tập 1: Để làm đường dẫn bắc ngang một con đê, người ta đúc một khối bê tông có kích thước như Hình 14. Tính chi phí để đúc khối bê tông đó, biết rằng chi phí để đúc 1 m³ bê tông là 1,2 triệu đồng.

Lời giải:

Khối bê tông trên là hình lăng trụ đứng có đáy là hình thang với độ dài hai cạnh đáy lần lượt là 2 m và 11 m; chiều cao là 4 m.

Diện tích đáy của khối bê tông là:

$\frac{\left(2+11\right).4}{2}$ = 26 (m²).

Thể tích của khối bê tông là: 26 . 6 = 156 (m³).

Chi phí để đúc khối bê tông đó là:

156 . 1,2 = 187,2 (triệu đồng).

Vậy cần 187,2 triệu đồng để đúc được khối bê tông đó.

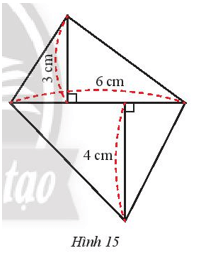
Bài 6 trang 63 Toán lớp 7 Tập 1: Một hình lăng trụ đứng tứ giác có kích thước đáy như Hình 15, biết chiều cao của lăng trụ là 7 cm. Tính thể tích của hình lăng trụ.

Lời giải:

Diện tích tam giác có đáy 6 cm, chiều cao tương ứng 3 cm là:

$\frac{3.6}{2}$ = 9 (cm²).

Diện tích tam giác có đáy 6 cm, chiều cao tương ứng 4 cm là:

$\frac{4.6}{2}$ = 12 (cm²).

Diện tích đáy của hình lăng trụ là: 9 + 12 = 21 (cm²).

Thể tích của hình lăng trụ đó là:

21 . 7 = 147 (cm³).

Vậy thể tích của hình lăng trụ đó là 147 cm³.