Trong các số 2, 3, 5, 9, số nào là ước của n với: a) n = 4 536
Lời giải Bài 2 trang 39 Toán 6 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 6.
Bài 2 trang 39 Toán lớp 6 Tập 1: Trong các số 2, 3, 5, 9, số nào là ước của n với:
a) n = 4 536;
b) n = 3 240;
c) n = 9 805?
Lời giải:
a) n = 4 536
+ Vì số 4 536 có chữ số tận cùng là 6 nên số này chia hết cho 2 và không chia hết cho 5.
+ Số 4 536 có tổng các chữ số là 4 + 5 + 3 + 6 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 4 536 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 4 536 là 2; 3; 9.
b) n = 3 240
+ Số 3 240 có chữ số tận cùng là 0 nên số này chia hết cho cả 2 và 5.
+ Số 3 240 có tổng các chữ số là 3 + 2 + 4 + 0 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 3 240 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 3 240 là 2; 3; 5; 9.
c) n = 9 805
+ Số 9 805 có chữ số tận cùng là 5 nên số này chia hết cho 5 và không chia hết cho 2.
+ Số 9 805 có tổng các chữ số là 9 + 8 + 0 + 5 = 22 không chia hết cho cả 3 và 9 nên số 9 805 không chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 9 805 là 5.
Xem thêm các bài giải sách giáo khoa Toán lớp 6 bộ sách Cánh Diều hay, chi tiết khác:
Hoạt động 1 trang 38 Toán lớp 6 Tập 1: a) Thực hiện phép tính 123 : 3 và nêu quan hệ chia hết của 123 với 3...
Luyện tập 1 trang 38 Toán lớp 6 Tập 1: Viết một số có hai chữ số sao cho: a) Số đó chia hết cho 3 và 5; b) Số đó chia hết cho cả ba số 2, 3, 5...
Hoạt động 2 trang 39 Toán lớp 6 Tập 1: a) Thực hiện phép tính 135 : 9 và nêu quan hệ chia hết của 135 với 9...
Luyện tập 2 trang 39 Toán lớp 6 Tập 1: Viết một số có hai chữ số sao cho: a) Số đó chia hết cho 2 và 9; b) Số đó chia hết cho cả ba số 2, 5, 9...
Bài 1 trang 39 Toán lớp 6 Tập 1: Cho các số 104, 627, 3 114, 5 123, 6 831 và 72 102. Trong các số đó: a) Số nào chia hết cho 3? Vì sao?...
Bài 2 trang 39 Toán lớp 6 Tập 1: Trong các số 2, 3, 5, 9, số nào là ước của n với: a) n = 4 536; b) n = 3 240; c) n = 9 805?...
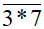chia hết cho 3; 
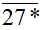chia hết cho 9...
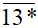chia hết cho 5 và 9; 
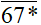chia hết cho 2 và 3...Bài viết liên quan
- Giải Toán lớp 6 Cánh diều Bài 10: Số nguyên tố. Hợp số
- Giải Toán lớp 6 Cánh diều Bài 11: Phân tích một số ra thừa số nguyên tố
- Giải Toán lớp 6 Cánh diều Bài 12: Ước chung và ước chung lớn nhất
- Giải Toán lớp 6 Cánh diều Bài 13: Bội chung và bội chung nhỏ nhất
- Giải Toán lớp 6 Cánh diều Bài tập cuối chương 1
