Giải Toán lớp 6 Cánh diều Bài 9: Dấu hiệu chia hết cho 3, cho 9
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9 sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Bài 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9
Trả lời câu hỏi giữa bài
Lời giải:
Ta giải quyết bài tập này sau khi học xong bài "Dấu hiệu chia hết cho 3, cho 9".
Theo đề bài ta thấy năm cần tìm thuộc thế kỉ XX, mà thế kỷ XX là khoảng thời gian tính từ thời điểm năm 1901 đến hết năm 2000 (bằng 100 năm).
Mà năm cần tìm được viết từ các chữ số lẻ khác nhau nên nó có dạng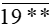 
(với * là các số tự nhiên lẻ từ 3 đến 7)
Ta có: 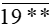chia hết cho 5 nên nó phải có chữ số tận cùng là 0 hoặc 5, nhưng số đó được viết từ các chữ số lẻ khác nhau nên chữ số tận cùng của 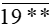phải là 5.
Khi đó số cần tìm có dạng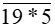 
Các chữ số lẻ còn lại thỏa mãn * là 3, 7
TH1. * = 3 khi đó ta có số 1935 với 1 + 9 + 3 + 5 = 18 chia hết cho 9. Hay 1935 chia hết cho 9 (không thỏa mãn)
TH2. * = 7 khi đó ta có số 1975 với 1 + 9 + 7 + 5 = 22 không chia hết cho 9, mà 22 chia 9 dư 4 nên 1975 chia cho 9 dư 4.
Vậy năm cần tìm là năm 1975.
Hoạt động 1 trang 38 Toán lớp 6 Tập 1:
a) Thực hiện phép tính 123 : 3 và nêu quan hệ chia hết của 123 với 3.
b) Tìm tổng S các chữ số của 123 và nêu quan hệ chia hết của S với 3.
Lời giải:
a) Ta có: 123 : 3 = 41
Do đó số 123 là số chia hết cho 3.
b) Tổng các chữ số của số 123 là: S = 1 + 2 + 3 = 6.
Ta có: 6 : 3 = 2
Do đó số 6 chia hết cho 3 hay S chia hết cho 3.
Luyện tập 1 trang 38 Toán lớp 6 Tập 1: Viết một số có hai chữ số sao cho:
b) Số đó chia hết cho cả ba số 2, 3, 5.
Lời giải:
a) Số chia hết cho 5 là số có chữ số tận cùng là 0 hoặc 5.
Số chia hết cho 3 là số có tổng các chữ số chia hết cho 3.
Do đó số chia hết cho 3 và 5 là số có tổng các chữ số chia hết cho 3 và có chữ số tận cùng là 0 hoặc 5.
Vậy một số có hai chữ số thỏa mãn số đó chia hết cho 3 và 5 là: 15 (hoặc các em có thể chọn một trong các số 30; 45; 60; 75; 90).
b) Số chia hết cho cả 2 và 5 là số có chữ số tận cùng là 0.
Số chia hết cho 3 là số có tổng các chữ số chia hết cho 3.
Do đó số chia hết cho cả ba số 2; 3; 5 là các số có tổng các chữ số chia hết cho 3 và có chữ số tận cùng là 0.
Vậy một số có hai chữ số thỏa mãn số đó chia hết cho cả ba số 2; 3 và 5 là: 30 (hoặc các em có thể chọn số 60 hoặc 90).
Hoạt động 2 trang 39 Toán lớp 6 Tập 1:
a) Thực hiện phép tính 135 : 9 và nêu quan hệ chia hết của 135 với 9.
b) Tìm tổng S các chữ số của 135 và nêu quan hệ chia hết của S với 9.
Lời giải:
a) Ta có: 135 : 9 = 15
Do đó số 135 chia hết cho 9.
b) Tổng các chữ số của 135 là: S = 1 + 3 + 5 = 9
Ta có 9 : 9 = 1
Vậy số 9 chia hết cho 9 hay S chia hết cho 9.
Luyện tập 2 trang 39 Toán lớp 6 Tập 1: Viết một số có hai chữ số sao cho:
b) Số đó chia hết cho cả ba số 2, 5, 9.
Lời giải:
a) Số chia hết cho 2 là các số có chữ số tận cùng là 0; 2; 4; 6; 8.
Số chia hết cho 9 là các số có tổng các chữ số chia hết cho 9.
Do đó các số chia hết cho 2 và 9 là các số có tổng các chữ số chia hết cho 9 và có chữ số tận cùng là 0; 2; 4; 6; 8.
Vậy một số có hai chữ số thỏa mãn số đó chia hết cho 2 và 9 là: 18 (hoặc các em có thể chọn một trong các số 36; 54; 72; 90).
b) Số chia hết cho cả 2 và 5 là các số có chữ số tận cùng là 0.
Số chia hết cho 9 là các số có tổng các chữ số chia hết cho 9.
Do đó các số chia hết cho cả ba số 2; 5 và 9 là các số có tổng các chữ số chia hết cho 9 và có chữ số tận cùng là 0.
Vậy một số có hai chữ số thỏa mãn số đó chia hết cho cả ba số 2; 5; 9 là: 90.
Bài tập
a) Số nào chia hết cho 3? Vì sao?
b) Số nào không chia hết cho 3? Vì sao?
c) Số nào chia hết cho 9? Vì sao?
d) Số nào chia hết cho 3, nhưng không chia hết cho 9? Vì sao?
Lời giải:
Ta áp dụng dấu hiệu chia hết cho 3 và dấu hiệu chia hết cho 9 để thực hiện bài tập này.
a) Trong các số đã cho ta có:
+ Số 627 chia hết cho 3 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3.
+ Số 3 114 chia hết cho 3 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 3.
+ Số 6 831 chia hết cho 3 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 3.
+ Số 72 102 chia hết cho 3 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3.
b) Ta có:
+ Số 104 không chia hết cho 3 vì tổng các chữ số 1 + 0 + 4 = 5 không chia hết cho 3.
+ Số 5 123 không chia hết cho 3 vì tổng các chữ số 5 + 1 + 2 + 3 = 11 không chia hết cho 3.
c) Ta có:
+ Số 3 114 chia hết cho 9 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 9.
+ Số 6 831 chia hết cho 9 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 9.
d) Ta có:
+ Số 627 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3 nhưng không chia hết cho 9.
+ Số 72 102 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3 nhưng không chia hết cho 9.
Bài 2 trang 39 Toán lớp 6 Tập 1: Trong các số 2, 3, 5, 9, số nào là ước của n với:
Lời giải:
a) n = 4 536
+ Vì số 4 536 có chữ số tận cùng là 6 nên số này chia hết cho 2 và không chia hết cho 5.
+ Số 4 536 có tổng các chữ số là 4 + 5 + 3 + 6 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 4 536 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 4 536 là 2; 3; 9.
b) n = 3 240
+ Số 3 240 có chữ số tận cùng là 0 nên số này chia hết cho cả 2 và 5.
+ Số 3 240 có tổng các chữ số là 3 + 2 + 4 + 0 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 3 240 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 3 240 là 2; 3; 5; 9.
c) n = 9 805
+ Số 9 805 có chữ số tận cùng là 5 nên số này chia hết cho 5 và không chia hết cho 2.
+ Số 9 805 có tổng các chữ số là 9 + 8 + 0 + 5 = 22 không chia hết cho cả 3 và 9 nên số 9 805 không chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 9 805 là 5.
Bài 3 trang 39 Toán lớp 6 Tập 1: Tìm chữ số thích hợp ở dấu * để số:
Lời giải:
a) Vì * là một chữ số trong số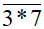 
nên * phải là một trong các số: 0; 1; 2; …; 9.
Số 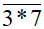chia hết cho 3 nên tổng các chữ số của số 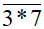là (3 + * + 7) = (10 + *) phải là số chia hết cho 3.
Thử thay * lần lượt bằng các số 0; 1; 2; …; 9, ta thấy các số thỏa mãn là 2; 5; 8.
Vậy các chữ số thích hợp điền vào dấu * để số 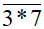chia hết cho 3 là: 2; 5; 8.
b) Vì * là một chữ số trong số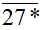 
nên * phải là một trong các số: 0; 1; 2; …; 9.
Số 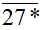chia hết cho 9 nên tổng các chữ số của số 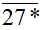là (2 + 7 + *) = (9 + *) phải là số chia hết cho 9.
Thử thay * lần lượt bằng các số 0; 1; 2; …; 9, ta thấy các số thỏa mãn là 0; 9.
Vậy các chữ số thích hợp điền vào dấu * để số 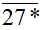chia hết cho 9 là: 0; 9.
Bài 4 trang 39 Toán lớp 6 Tập 1: Tìm chữ số thích hợp ở dấu * để số:
Lời giải:
a) Vì * là một chữ số trong số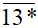 
nên * phải là một trong các số: 0; 1; 2; …; 9.
Số 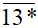chia hết cho 5 nên 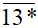phải có chữ số tận cùng là 0 hoặc 5, hay * phải là 0 hoặc 5.
Số 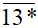chia hết cho 9 nên tổng các chữ số của số 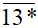là (1 + 3 + *) = (4 + *) phải là số chia hết cho 9.
Thay * lần lượt bằng các số 0; 5 ta được:
+) 4 + 0 = 4 không chia hết cho 9
+) 4 + 5 = 9 chia hết cho 9
Vậy chữ số thích hợp điền vào dấu * để số 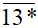chia hết cho cả 5 và 9 là: 5 hay * = 5.
b) Số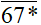 
chia hết cho 2 nên 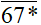phải có chữ số tận cùng là 0; 2; 4; 6; 8, hay * phải là một trong các số: 0; 2; 4; 6; 8.
Số 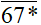chia hết cho 3 nên tổng các chữ số của số 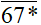là (6 + 7 + *) = (13 + *) phải là số chia hết cho 3.
Thay * lần lượt bằng các số 0; 2; 4; 6; 8 ta được:
+) 13 + 0 = 13 không chia hết cho 3
+) 13 + 2 = 15 chia hết cho 3
+) 13 + 4 = 17 không chia hết cho 3
+) 13 + 6 = 19 không chia hết cho 3
+) 13 + 8 = 21 chia hết cho 3
Vậy các chữ số thích hợp điền vào dấu * để số 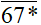chia hết cho cả 2 và 3 là: 2; 8 hay * = 2 hoặc * = 8.
a) Lớp nào có thể xếp thành 3 hàng với số học sinh ở mỗi hàng là như nhau?
b) Lớp nào có thể xếp thành 9 hàng với số học sinh ở mỗi hàng là như nhau?
Lời giải:
a) Để số học sinh của một lớp có thể xếp thành ba hàng với số học sinh ở mỗi hàng là như nhau thì tổng số học sinh của lớp đó phải là số chia hết cho 3.
Trong các số 40; 45; 39; 44; 42 thì:
+ Số 45 chia hết cho 3 (vì 45 có tổng các chữ số là 4 + 5 = 9 chia hết cho 3)
+ Số 39 chia hết cho 3 (vì 39 có tổng các chữ số là 3 + 9 = 12 chia hết cho 3)
+ Số 42 chia hết cho 3 (vì 42 có tổng các chữ số là 4 + 2 = 6 chia hết cho 3)
Vậy các lớp 6B, 6C; 6E có thể xếp thành 3 hàng với số học sinh ở mỗi hàng là như nhau.
b) Để số học sinh của một lớp có thể xếp thành chín hàng với số học sinh ở mỗi hàng là như nhau thì tổng số học sinh của lớp đó phải là số chia hết cho 9.
Trong các số 40; 45; 39; 44; 42 thì chỉ có số 45 chia hết cho 9 (vì 45 có tổng các chữ số là 4 + 5 = 9 chia hết cho 9).
Vậy chỉ có lớp 6B có thể xếp thành 9 hàng với số học sinh ở mỗi hàng là như nhau.
c) Tổng số học sinh của cả 5 lớp 6A, 6B, 6C, 6D, 6E là:
40 + 45 + 39 + 44 + 42 = 210 (học sinh)
Ta có số 210 là số chia hết cho 3 (vì tổng các chữ số của số 210 là 2 + 1 + 0 = 3 chia hết cho 3)
Do đó tổng số học sinh của cả 5 lớp là số chia hết cho 3.
Vậy ta có thể xếp tất cả học sinh của 5 lớp đó thành 3 hàng với số học sinh ở mỗi hàng là như nhau.
d) Ta có số 210 là số không chia hết cho 9 (vì tổng các chữ số của số 210 là 2 + 1 + 0 = 3 không chia hết cho 9)
Do đó tổng số học sinh của cả 5 lớp là số không chia hết cho 9.
Vậy ta không thể xếp tất cả học sinh của 5 lớp đó thành 9 hàng với số học sinh ở mỗi hàng là như nhau.
Bài viết liên quan
- Giải Toán lớp 6 Cánh diều Bài 7: Quan hệ chia hết. Tính chất chia hết
- Giải Toán lớp 6 Cánh diều Bài 8: Dấu hiệu chia hết cho 2, cho 5
- Giải Toán lớp 6 Cánh diều Bài 10: Số nguyên tố. Hợp số
- Giải Toán lớp 6 Cánh diều Bài 11: Phân tích một số ra thừa số nguyên tố
- Giải Toán lớp 6 Cánh diều Bài 12: Ước chung và ước chung lớn nhất
