Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 6 Bài 5: Số thập phân sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Bài 5. Mời các bạn đón xem:
Giải bài tập Toán lớp 6 Bài 5: Số thập phân
Trả lời câu hỏi giữa bài
Những số - 0,4; - 0,2 có phải là các số thập phân không?
Trong các số - 0.4; - 0,2; 6,5; 5,4; 5,6 số nào lớn nhất? Số nào nhỏ nhất?
Lời giải:
Sau bài học này ta có thể trả lời được:
Các số - 0,4; -0,2 là các số thập phân.
Ta so sánh các số thập phân trên bằng cách chia làm hai nhóm:
- Nhóm 1 gồm các số thập phân âm: -0,4 và – 0,2;
- Nhóm 2 gồm các số thập phân dương: 5,4; 5,6 và 6,5.
Vì số thập phân âm luôn nhỏ hơn số thập phân dương nên ta sẽ so sánh các số trong từng nhóm với nhau.
Nhóm 1: Số đối với số thập phân – 0,4 là 0,4, còn số đối với số thập phân -0,2 là 0,2.
Hai số thập phân này có cùng phần nguyên, kể từ trái sang cặp chữ số cùng hàng ở sau dấu phẩy khác nhau là cặp chữ số ở hàng phần mười. Do 4 > 2 nên 0,4 > 0,2 suy ra -0,4 < - 0,2.
Nhóm 2: 5,4 và 5,6 có cùng phần nguyên, kể từ trái sang cặp chữ số cùng hàng ở sau dấu phẩy khác nhau là cặp chữ số ở hàng phần mười. Do 4 < 6 nên 5,4 < 5,6.
Ta có 5 < 6 nên 5,6 < 6,5.
Do đó, ta có: 5,4 < 5,6 < 6,5.
Suy ra -0,4 < -0,2 < 5,4 < 5,6 < 6,5.
Vậy số thập phân lớn nhất là 6,5, số thập phân bé nhất là – 0,4.
Mẫu: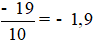 và được đọc là: âm một phẩy chín
và được đọc là: âm một phẩy chín
Lời giải:
Các phân số được viết dưới dạng số thập phân là:
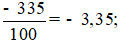
Đọc là: âm ba phẩy ba mươi lăm.
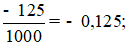
Đọc là: âm không phẩy một trăm hai lăm.
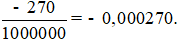
Đọc là: âm không phẩy không không không hai bảy không.
Luyện tập 1 trang 45 Toán lớp 6 Tập 2: Viết các phân số và hỗn số sau dưới dạng số thập phân:
Lời giải:
Các phân số, hỗn số được viết dưới dạng số thập phân là:
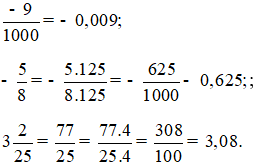
Luyện tập 2 trang 45 Toán lớp 6 Tập 2: Viết các số thập phân sau dưới dạng phân số tối giản:
Lời giải:
Viết các phân số dưới dạng phân số tối giản là:
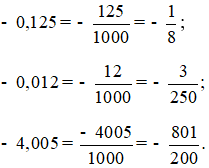
Hoạt động 2 trang 46 Toán lớp 6 Tập 2: So sánh:
Lời giải:
a) Vì 508 < 509 nên 508,99 < 509,01.
Vậy 508,99 < 509,01.
b) Ta có: 315 = 315 và kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần trăm. Do 6 < 9 nên 315,267 < 315,29.
Vậy 315,267 < 315,29.
Hoạt động 3 trang 47 Toán lớp 6 Tập 2: Nêu cách so sánh hai số nguyên âm.
Lời giải:
Cách so sánh hai số nguyên âm a và b:
- Tìm số đối của hai số nguyên a và b.
- Ta sẽ so sánh số đối của hai số nguyên âm a và b với nhau (số nguyên âm nào có số đối lớn hơn thì sẽ nhỏ hơn).
Luyện tập 3 trang 47 Toán lớp 6 Tập 2: Viết các số sau theo thứ tự giảm dần:
-120,341; 36,095; 36,1; -120,34.
Lời giải:
Ta sẽ chia các số thập phân trên thành hai nhóm:
- Nhóm 1 gồm các số thập phân âm: -120,341; -120,34.
- Nhóm 2 gồm các số thập phân dương: 36,095; 36,1.
Vì các số thập phân âm luôn nhỏ hơn các số thập phân dương nên ta chỉ cần so sánh các số trong từng nhóm với nhau.
Ở nhóm 1: Ta có số đối của số thập phân -120,341 là 120,341 và số đối của số thập phân – 120,34 là 120,34. Ta có: 120 = 120, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần nghìn. Do 1 > 0 nên 120,341 > 120,34 hay -120,341 < -120,34.
Ở nhóm 2: Ta có 36 = 36, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 1 nên 36,095 < 36,1.
Suy ra -120,341 < -120,34 < 36,095 < 36,1.
Vậy 36,1; 36,095; -120,34; -120,341.
Bài tập
Bài 1 trang 47 Toán lớp 6 Tập 2: Viết các phân số và hỗn số sau dưới dạng số thập phân: 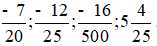
Lời giải:
Các phân số và hỗn số viết dưới dạng số thập phân là:

Lời giải:
Các số thập phân được viết dưới dạng phân số tối giản là:
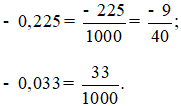
Bài 3 trang 47 Toán lớp 6 Tập 2: Viết các số sau theo thứ tự tăng dần:
b) 73,059; - 49,037; - 49,307.
Lời giải:
a) Ta sẽ so sánh từng cặp số với nhau:
+) 7,012 và 7,102.
Ta có 7 = 7, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 1 nên 7,012 < 7,102 (1).
+) 7,012 và 7,01
Ta có 7 = 7, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần nghìn. Do 0 < 2 nên 7,012 > 7,01 (2).
Từ (1) và (2) suy ra: 7,01 < 7,012 < 7,102.
Vậy các số theo thứ tự tăng dần là: 7,01; 7,012; 7,102.
b) Vì số thập phân âm luôn bé hơn số thập phân dương nên ta chỉ cần so sánh -49,037 và -49,307.
Ta có số đối của số thập phân -49,037 là 49,037 và số đối của số thập phân -49,307 là 49,307.
Ta có: 49 = 49, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 3 nên 49,037 < 49,307 hay -49,037 > -49,307.
Suy ra: -49,307 < -49,037 < 73,059.
Vậy các số theo thứ tự tăng dần là: -49,307; -49,037; 73,059.
Bài 4 trang 47 Toán lớp 6 Tập 2: Viết các số sau theo thứ tự giảm dần:
a) 9,099; 9,009; 9,090; 9,990;
b) - 6,27; - 6,207; - 6,027; - 6,277.
Lời giải:
a) Ta có: 9 = 9, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 9 nên 9,990 là số lớn nhất.
Các số còn lại, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần trăm. Do 0 < 9 nên 9,009 là số nhỏ nhất.
Hai số còn lại là 9,099; 9,090, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần nghìn. Do 0 < 9 nên 9,090 < 9,099.
Suy ra 9,009 < 9,090 < 9,099 < 9,990.
Vậy các số theo thứ tự giảm dần là: 9,990; 9,099; 9,090; 9,009.
b) Vì các số - 6,27; - 6,207; - 6,027; - 6,277 đều là số thập phân âm nên ta sẽ chuyển qua so sánh các số đối lần lượt là: 6,27; 6,207; 6,027; 6,277.
Ta có 6 = 6, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 2 nên số 6,027 là số nhỏ nhất.
Đối với các số còn lại 6,27; 6,207; 6,277, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần trăm. Do 0 < 7 nên 6,207 là số nhỏ nhất trong dãy này.
Còn lại hai số 6,27; 6,277, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần nghìn. Do 0 < 7 nên 6,27 < 6,277.
Suy ra 6,027 < 6,207 < 6,27 < 6,277 hay - 6,027 > - 6,207 > - 6,27 > - 6,277.
Vậy các số theo thứ tự giảm dần là: - 6,027; - 6,207; - 6,27; - 6,277.
Mai Anh: 31,42 giây; Ngọc Mai: 31,48 giây; Phương Hà: 31,09 giây.
Vận động viên nào đã về nhất? Về nhì? Về ba?
Lời giải:
Ta cần so sánh thời gian hoàn thành cuộc đua của các vận động viên tham gia:
Ta có 31 = 31 = 31, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 4 nên 31,09 là số bé nhất.
Còn hai số còn lại 31,42 và 31,48, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần trăm. Do 2 < 8 nên 31,42 < 31,48.
Từ đó suy ra: 31,09 < 31,42 < 31,48.
Vận động viên về nhất là vận động viên đến đích sớm hơn hay mất ít thời gian nhất để hoàn thành cuộc đua. Vận động viên về nhì là vận động viên mất ít thời gian tiếp theo. Vận động viên về ba là vận động viên mất nhiều thời gian nhất trong ba vận động viên.
Vậy vận động viên về nhất là bạn Phương Hà, vận động viên về nhì là bạn Mai Anh, vận động viên về ba là bạn Ngọc Mai.


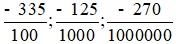 dưới dạng số thập phân và đọc các số thập phân đó theo mẫu.
dưới dạng số thập phân và đọc các số thập phân đó theo mẫu.