Bài tập cuối chương 7
Bộ 30 Bài tập cuối chương 7 có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài tập cuối chương 7.
Trắc nghiệm Toán 7 Bài tập cuối chương 7 - Cánh diều
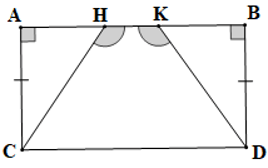
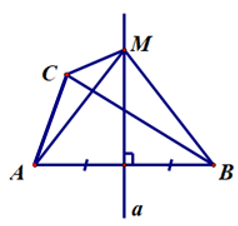
Câu 1. Cho hình vẽ sau:
Biết CH = 3,5 cm. Số đo cạnh DK là:
A. 2,5 cm;
B. 3,5 cm;
C. 4 cm;
D. 4,5 cm.
Đáp án: B
Giải thích:
Ta có:
• (hai góc kề bù);
• (hai góc kề bù)
Mà (giả thiết) nên
Vì ∆AHC vuông tại A nên (trong tam giác vuông, hai góc nhọn phụ nhau)
Vì ∆BKD vuông tại B nên (trong tam giác vuông, hai góc nhọn phụ nhau)
Mà (chứng minh trên) nên
Xét ∆AHC và ∆BKD có:
(= 90°)
(chứng minh trên),
AC = BD (giả thiết),
Do đó ∆AHC = ∆BKD (cạnh góc vuông – góc nhọn kề)
Suy ra CH = DK (hai cạnh tương ứng)
Mà CH = 3,5 cm nên DK = 3,5 cm.
Câu 2. Cho tam giác MNP có . Số đo góc N là:
A. 30°;
B. 45°;
C. 60°;
D. 105°.
Đáp án: B
Giải thích:
Xét tam giác MNP có (tổng ba góc trong một tam giác)
Vì nên
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra
Vậy số đo góc N bằng 45°.
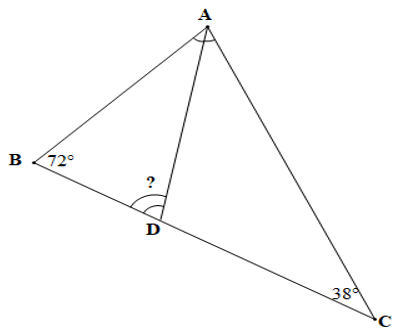
Câu 3. Cho tam giác ABC có . Tia phân giác góc A cắt cạnh BC tại D. Số đo góc ADB là:
A. 73°;
B. 55°;
C. 67°;
D. 35°.
Đáp án: A
Giải thích:
Xét tam giác ABC có (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Mà tia AD là tia phân giác của
Nên (tính chất tia phân giác của một góc)
Suy ra
Mặt khác: là góc ngoài của tam giác ACD tại đỉnh D
Nên (tính chất góc ngoài của một tam giác)
Hay
Vậy số đo góc ADB là 73°.
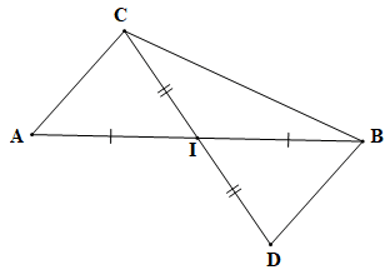
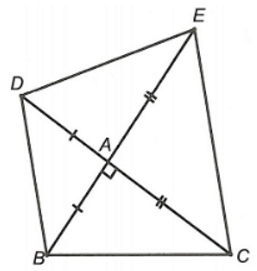
Câu 4. Cho tam giác ABC có I là trung điểm của AB. Khẳng định nào sau đây là đúng?
A. AC + BC ≤ 2CI;
B. AC + BC > 2CI;
C. AC + BC = CI;
D. AC + BC < 2CI.
Đáp án: B
Giải thích:
Trên tia đối của tia IC lấy điểm D sao cho ID = IC
Xét DACI và DBID có:
AI = BI (vì I là trung điểm của AB);
CI = DI;
(hai góc đối đỉnh).
Do đó DACI = DBDI (c.g.c)
Suy ra AC = BD (hai cạnh tương ứng)
Xét DBCD có: CD < BC + BD (bất đẳng thức trong tam giác)
Hay 2.CI < BC + BD
Do đó 2CI < BC + AC.
Câu 5. Cho một tam giác cân có độ dài hai cạnh (không bằng nhau) là 2 cm và 5 cm. Chu vi của tam giác đó là:
A. 9 cm;
B. 10 cm;
C. 11 cm;
D. 12 cm.
Đáp án: D
Giải thích:
Giả sử tam giác ABC cân có AB = 2 cm và BC = 5 cm.
Áp dụng bất đẳng thức cho tam giác ABC ta có:
BC – AB < AC < BC + AB
Hay 5 – 2 < AC < 5 + 2
Suy ra 3 < AC < 7 (*)
Vì tam giác ABC là tam giác cân (giả thiết)
Mà AB = 2 cm và BC = 5 cm nên không thể cân tại B.
Do đó có hai trường hợp có thể xảy ra:
• Trường hợp 1: DABC cân tại A.
Suy ra AB = AC.
Mà AB = 2 cm nên AC = 2 cm (không thỏa mãn điều kiện (*))
Nên AB = 2 cm hoặc AB = 5 cm (2)
• Trường hợp 2: DABC cân tại C.
Suy ra CA = CB.
Mà BC = 5 cm nên AC = 5 cm (thỏa mãn điều kiện (*))
Vậy AC = 5 cm.
Khi đó chu vi tam giác ABC là:
AB + AC + BC = 2 + 5 + 5 = 12 (cm).
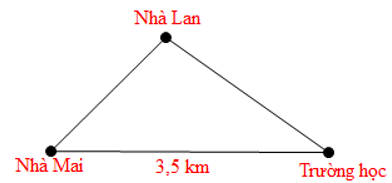
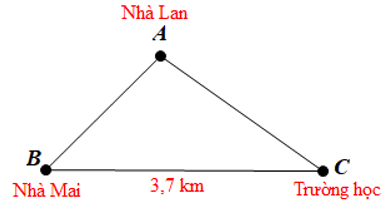
Câu 6. Ba vị trí của nhà Mai, nhà Lan và trường học được mô tả như hình vẽ dưới đây.
Trong buổi sáng hôm nay, Mai phải đến nhà Lan để lấy đồ trước khi đến trường.
Bạn Mai nói rằng tổng quãng đường mà Mai đã đi khoảng 3 km.
Bạn Lan nói rằng tổng quãng đường mà Mai đã đi khoảng 4 km.
Bạn Minh nói rằng tổng quãng đường mà Mai đã đi khoảng 5 km.
Chọn khẳng định đúng:
A. Chỉ bạn Mai nói sai;
B. Chỉ bạn Lan nói sai;
C. Bạn Lan và Minh nói sai.
D. Cả ba bạn nói sai.
Đáp án: A
Giải thích:
Đặt ba điểm tại ba vị trí như hình vẽ trên.
Theo bất đẳng thức ta có:
AB + AC > BC
Nên AB + AC > 3,7 cm.
Do đó tổng quãng đường từ nhà Mai đến nhà Lan rồi từ nhà Lan tới trường học phải lớn hơn 3,7 km.
Vậy nên bạn Mai đã nói sai.
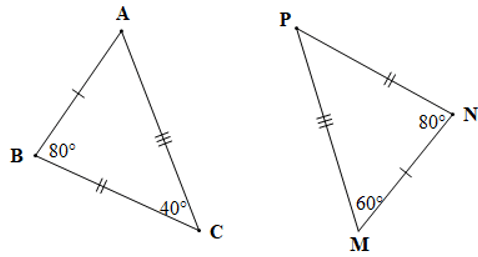
Câu 7. Cho hai tam giác ABC và MNP như hình vẽ dưới đây:
Khẳng định nào sau đây là đúng?
A. ∆ABC = ∆MNP;
B. ∆ABC = ∆MPN;
C. ∆ABC = ∆NMP;
D. ∆ABC = ∆NPM.
Đáp án: A
Giải thích:
Xét tam giác ABC ta có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Xét tam giác MNP ta có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Khi đó: tam giác ABC và tam giác MNP có:
+) AB = NM, BC = NP, AC = MP;
+)
Do đó hai tam giác ABC và MNP bằng nhau và được kí hiệu là ∆ABC = ∆MNP.
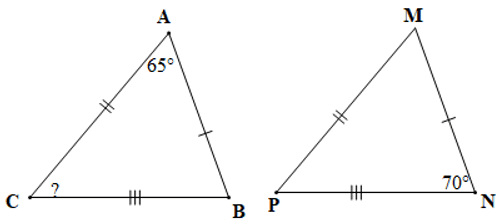
Câu 8. Cho hình vẽ bên dưới:
Số đo góc C và góc M lần lượt là:
A. 45° và 65°;
B. 65° và 45°;
C. 55° và 70°;
D. 70° và 55°.
Đáp án: A
Giải thích:
Xét tam giác ABC và tam giác MNP có:
AB = MN, BC = NP, AC = MP (giả thiết)
Suy ra ∆ABC = ∆MNP (c.c.c)
Do đó , , (các cặp góc tương ứng)
Mà , nên
Xét tam giác ABC có: (tổng ba góc trong một tam giác)
Suy ra
Hay
Vậy số đo góc C và góc M lần lượt là: 45° và 65°.
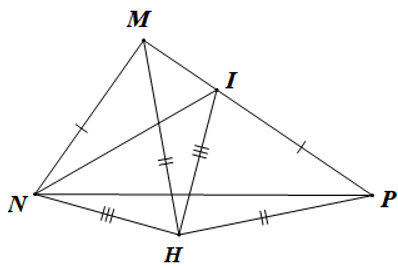
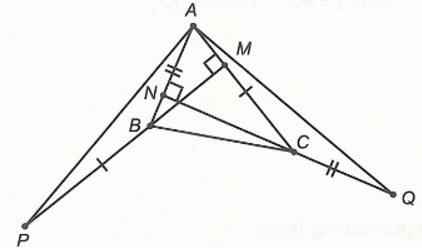
Câu 9. Cho tam giác MNP có MN < MP. Lấy điểm I trên cạnh MP sao cho MN = PI. Gọi H là điểm sao cho HM = HP, HN = HI.
Khẳng định nào sau đây là đúng?
A. ∆MNH = ∆PIH;
B. ∆MNH = ∆PHI;
C. ;
D. .
Đáp án: A
Giải thích:
Xét ∆MNH và ∆PIH ta có:
HM = HP (giả thiết);
HN = HI (giả thiết);
MN = PI (giả thiết).
Do đó ∆MNH = ∆PIH (c.c.c)
Suy ra (các cặp góc tương ứng)
Câu 10. Qua trung điểm H của đoạn thẳng BC, kẻ đường thẳng vuông góc với BC, trên đường thẳng vuông góc đó lấy hai điểm A và I. Nối CA, AB, IB, IC. Phát biểu nào sau đây là đúng nhất:
A. ∆ABH = ∆ACH;
B. ∆IBH = ∆ICH;
C. ∆BAI = ∆CAI;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
Vì A nằm trên đường thẳng vuông góc với CB tại H nên ta có:
Vì I nằm trên đường thẳng vuông góc với CB tại H nên ta có:
+) Xét ∆ABH và ∆ACH có:
(chứng minh trên),
AH là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ∆ABH = ∆ACH (hai cạnh góc vuông)
Do đó đáp án A đúng
Vì ∆ABH = ∆ACH (chứng minh trên)
Suy ra AB = AC (hai cạnh tương ứng) và (hai góc tương ứng)
+) Xét tam giác HCI và tam giác HBI có:
(chứng minh trên),
HI là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ∆ICH = ∆IBH (hai cạnh góc vuông)
Do đó đáp án B đúng
+) Xét tam giác BAI và tam giác CAI có:
AB = AC (chứng minh trên),
(do ),
AI là cạnh chung
Suy ra ∆BAI = ∆CAI (c.g.c)
Do đó đáp án C đúng.
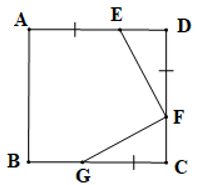
Câu 11. Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:
A. 45°;
B. 90°;
C. 60°;
D. 100°.
Đáp án: B
Giải thích:
Vì ABCD là hình vuông (giả thiết) nên AD = CD (tính chất hình vuông)
Do đó AE + ED = CF + FD
Mà AE = FD (giả thiết) nên ED = CF.
Xét ∆FED và ∆GFC có:
FD = CG (giả thiết),
(tính chất hình vuông),
ED = CF (chứng minh trên)
Do đó ∆FED = ∆GFC (hai cạnh góc vuông)
Suy ra (hai góc tương ứng)
Mà (trong tam giác FDE vuông tại D, hai góc nhọn phụ nhau)
Do đó
Mặt khác
Suy ra
Vậy
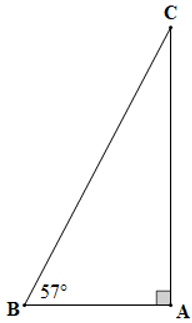
Câu 12. Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với mặt đất là 57°, khi đó độ nghiêng của chiếc thang đó so với bức tường là:
A. 55°;
B. 44°;
C. 33°;
D. 22°.
Đáp án: C
Giải thích:
Ta vẽ tam giác ABC vuông tại A có để mô tả hình ảnh chiếc thang dựa vào tường như đề bài.
Trong tam giác ABC vuông tại A ta có: (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra
Vậy độ nghiêng của chiếc thang so với bức tường là 33°.
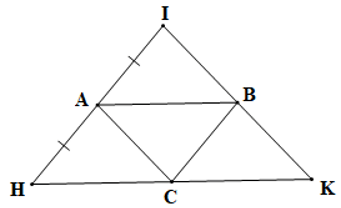
Câu 13. Cho tam giác HIK, A là trung điểm của IH. Đường thẳng qua A và song song với HK cắt IK tại B. Đường thẳng qua B và song song với IH cắt HK tại C. Khẳng định nào sau đây là đúng nhất ?
A. CH = KC;
B. ∆ABI = ∆CKB;
C. AI = BC;
D. Cả A, B , C đều đúng.
Đáp án: D
Giải thích:
• Vì AB // HK (giả thiết) nên (hai góc so le trong)
Vì BC // IH (giả thiết) nên (hai góc so le trong)
• Xét ∆ABC và ∆CHA có:
(chứng minh trên),
AC là cạnh chung,
(chứng minh trên)
Do đó ∆ABC = ∆CHA (g.c.g)
Suy ra BC = AH (hai cạnh tương ứng)
Mà AH = AI (do A là trung điểm của IH)
Do đó BC = AI nên đáp án C là đúng.
• Vì CH // AB (giả thiết) nên (hai góc đồng vị)
Vì IH // CB (giả thiết) nên và (các cặp góc đồng vị)
Do đó
Xét ∆ABI và ∆CKB có:
(chứng minh trên),
AI = BC (chứng minh trên),
(chứng minh trên),
Do đó ∆ABI = ∆CKB (g.c.g) nên đáp án B là đúng
Suy ra AB = KC (hai cạnh tương ứng)
Mà ∆ABC = ∆CHA (chứng minh trên)
Nên AB = CH (hai cạnh tương ứng)
Do đó CH = CK (= AB) nên đáp án A là đúng
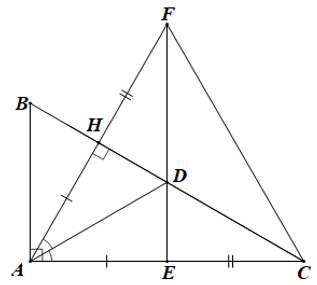
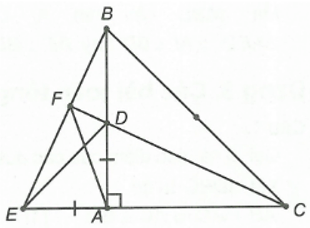
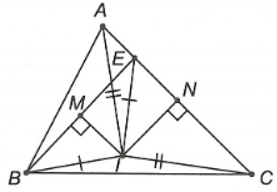
Câu 14. Cho ∆ABC vuông tại A có . Kẻ AH ⊥ BC tại H và tia phân giác AD của (D ∈ BC). Trên cạnh AC lấy điểm E sao cho AE = AH. Trên tia đối của tia HA lấy điểm F sao cho HF = EC. Khẳng định nào sau đây đúng nhất?
A. ∆ADH = ∆ADE;
B. DE ⊥ AC;
C. ∆ACF đều;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
Ta xét từng đáp án:
Đáp án A:
Xét ∆ADH và ∆ADE, có:
AH = AE (giả thiết).
(do AD là phân giác của ).
AD là cạnh chung.
Do đó ∆ADH = ∆ADE (c.g.c)
Suy ra đáp án A đúng.
Đáp án B:
∆ADH = ∆ADE (chứng minh trên).
Suy ra (cặp góc tương ứng).
Mà (do AH ⊥ HD).
Do đó .
Khi đó ta có DE ⊥ AE hay DE ⊥ AC.
Do đó đáp án B đúng.
Đáp án C:
Ta có AH = AE (giả thiết) và HF = EC (giả thiết).
Suy ra AH + HF = AE + EC.
Do đó AF = AC.
Khi đó ta có ∆ACF cân tại A (1).
Vì ∆AHC vuông tại H nên .
Do đó (2).
Từ (1), (2), ta suy ra ∆ACF là tam giác đều.
Do đó đáp án C đúng.
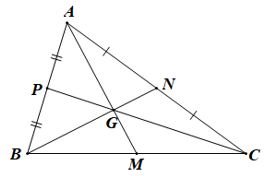
Câu 15. Cho hình vẽ sau:
Biết AM = 3 cm. Độ dài đoạn thẳng GM là:
A. 1 cm;
B. 2 cm;
C. 3 cm;
D. 4,5 cm.
Đáp án: A
Giải thích:
Trên hình vẽ, hai đường trung tuyến BN và CP cắt nhau tại G
Nên G là trọng tâm tam giác ABC
Do đó (tính chất trọng tâm)
Suy ra
Mà AM = 3 cm
Nên GM = 1 cm.
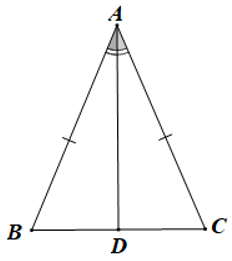
Câu 16. Cho ∆ABC cân tại A, tia phân giác trong của cắt BC tại D. Khẳng định nào dưới đây sai?
A. D là trung điểm BC;
B. ;
C. ∆ADB = ∆ADC;
D. .
Đáp án: D
Giải thích:
Xét ∆ADB và ∆ADC, có:
AD là cạnh chung,
(do AD là tia phân giác của ),
AB = AC (do ∆ABC cân tại A).
Do đó ∆ADB = ∆ADC (c.c.c).
Suy ra đáp án C đúng.
Ta có ∆ADB = ∆ADC (chứng minh trên).
Suy ra BD = CD và (cặp cạnh và cặp góc tương ứng).
Vì BD = CD nên D là trung điểm BC.
Do đó đáp án A đúng.
Ta có (hai góc kề bù).
Suy ra .
Do đó AD ⊥ BC.
∆ABD vuông tại D: .
Mà (AD là phân giác của ).
Suy ra .
Do đó đáp án B đúng.
Ta có .
Suy ra .
Do đó .
Do đó đáp án D sai.
Câu 17. Giao điểm của ba đường trung tuyến trong một tam giác được gọi là gì?
A. Điểm cách đều ba đỉnh của tam giác đó;
B. Trọng tâm;
C. Điểm cách đều ba cạnh của tam giác đó;
D. Trực tâm.
Đáp án: B
Giải thích:
Điểm cách đều ba đỉnh của tam giác là giao điểm của ba đường trung trực của tam giác đó.
Trọng tâm là giao điểm của ba đường trung tuyến của một tam giác.
Điểm cách đều ba cạnh của tam giác là giao điểm của ba đường phân giác của tam giác đó.
Trực tâm là giao điểm của ba đường cao của một tam giác.
Câu 18. Trong một tam giác, trực tâm là giao điểm của ba đường gì?
A. Trung trực;
B. Phân giác;
C. Trung tuyến;
D. Đường cao.
Đáp án: D
Giải thích:
Trong một tam giác, trực tâm là giao điểm của ba đường cao.
Do đó ta chọn phương án D.
Câu 19. Cho các phát biểu:
(I) Ba đường trung tuyến của một tam giác đồng quy tại một điểm.
(II) Ba đường phân giác của một tam giác đồng quy tại một điểm.
(III) Ba đường trung trực của một tam giác đồng quy tại một điểm.
(IV) Ba đường cao của một tam giác đồng quy tại một điểm.
Số các phát biểu đúng là:
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: D
Giải thích:
Ta xét từng phát biểu:
Ba đường trung tuyến của một tam giác đồng quy tại một điểm, điểm đó là trọng tâm của tam giác đó.
Do đó phát biểu (I) đúng.
Ba đường phân giác của một tam giác đồng quy tại một điểm, điểm đó cách đều ba cạnh của tam giác đó.
Do đó phát biểu (II) đúng.
Ba đường trung trực của một tam giác đồng quy tại một điểm, điểm đó cách đều ba đỉnh của tam giác đó.
Do đó phát biểu (III) đúng.
Ba đường cao của một tam giác đồng quy tại một điểm, điểm đó được gọi là trực tâm của tam giác đó.
Do đó phát biểu (IV) đúng.
Vậy có 4 phát biểu đúng, ta chọn phương án D.
Câu 20. Cho ∆ABC vuông tại A. Trực tâm của ∆ABC là điểm nào?
A. Điểm A;
B. Điểm B;
C. Điểm C;
D. Không có trực tâm.
Đáp án: A
Giải thích:
Trong một tam giác, trực tâm là giao điểm của ba đường cao.
Để xác định trực tâm của một tam giác, ta cần xác định giao điểm của ít nhất hai đường cao của tam giác đó.
Vì ∆ABC vuông tại A nên ta có AB ⊥ AC tại A.
Suy ra ∆ABC có hai đường cao là AB và AC.
Hai đường cao này cắt nhau tại A.
Do đó A là trực tâm của ∆ABC.
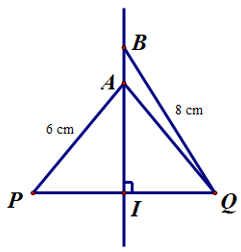
Câu 21. Cho đoạn thẳng PQ. Gọi A và B là hai điểm thuộc đường trung trực của đoạn PQ sao cho AP = 6 cm, BQ = 8 cm. Gọi I là giao điểm của PQ và AB. Khẳng định nào sau đây đúng nhất?
A. I là trung điểm của PQ;
B. AQ < BQ;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Đáp án: C
Giải thích:
• Vì AB là đường trung trực của đoạn thẳng PQ và AB cắt PQ tại I.
Ta suy ra I là trung điểm của PQ.
Do đó đáp án A đúng.
• Vì A nằm trên đường trung trực của đoạn thẳng PQ.
Nên A cách đều P, Q.
Suy ra AQ = AP = 6 cm.
Mà BQ = 8 cm.
Do đó đáp án B đúng.
Câu 22. Cho tam giác ABC (AC < BC), a là đường trung trực của đoạn thẳng AB. Lấy điểm M (M khác trung điểm của AB) nằm trên đường thẳng a.
So sánh độ dài của MA + MC với độ dài đoạn BC.
A. MA + MC < BC;
B. MA + MC > BC;
C. MA + MC = BC;
D. Không thể so sánh được.
Đáp án: B
Giải thích:
Vì M nằm trên đường trung trực của đoạn thẳng AB nên MA = MB (1).
Xét ∆CMB, có: MC + MB > BC (bất đẳng thức tam giác) (2).
Từ (1), (2), ta suy ra MC + MA > BC.
Câu 23. ∆ABC có . Gọi O là trung điểm của BC. Vẽ BD ⊥ AO, CE ⊥ AO (D, E thuộc đường thẳng AO). So sánh AB và .
A. ;
B. ;
C. ;
D. Không thể so sánh được.
Đáp án: C
Giải thích:
• Xét ∆BOD và ∆COE, có:
,
OB = OC (do O là trung điểm của BC),
(hai góc đối đỉnh),
Do đó ∆BOD = ∆COE (cạnh huyền – góc nhọn).
Suy ra OD = OE (cặp cạnh tương ứng).
• ∆AOB có (giả thiết).
Ta suy ra OA là cạnh lớn nhất trong ba cạnh AO, OB, AB của ∆AOB.
Do đó AB < OA.
Khi đó ta có AB < AD + OD (1) và AB < AE – OE (2).
Lấy (1) + (2) vế theo vế, ta được:
2AB < AD + OD + AE – OE.
Suy ra 2AB < AD + AE + OD – OD (vì OD = OE (chứng minh trên)).
Do đó 2AB < AD + AE.
Vì vậy .
Câu 24. Cho ∆ABC vuông tại A (AB < AC). Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC. Khẳng định nào sau đây đúng nhất?
A. BC = DE;
B. ∆ABD vuông cân;
C. BD // CE;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
• Xét ∆ABC và ∆ADE, có:
AB = AD (giả thiết),
(hai góc đối đỉnh),
AC = AE (giả thiết).
Do đó ∆ABC = ∆ADE (c.g.c)
Suy ra BC = DE (cặp cạnh tương ứng).
Vì vậy đáp án A đúng.
• Xét ∆ABD có DA ⊥ AB (do ∆ABC vuông tại A).
Suy ra .
Do đó ∆ABD vuông tại A.
Lại có AB = AD (giả thiết).
Suy ra ∆ABD vuông cân tại A.
Do đó đáp án B đúng.
• Chứng minh tương tự, ta được ∆ACE vuông cân tại A.
Suy ra .
Mà hai góc này ở vị trí so le trong.
Do đó BD // CE.
Vì vậy đáp án C đúng.
Câu 25. Cho ∆ABC nhọn, hai đường cao BM và CN. Trên tia đối của tia BM, lấy điểm P sao cho BP = AC. Trên tia đối của tia CN, lấy điểm Q sao cho CQ = AB. Khẳng định nào sau đây đúng nhất?
A. ∆APQ vuông cân tại A;
B. ∆BAP = ∆CQA;
C. ;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
•Ta có:
+) (cùng phụ với );
+) (hai góc kề bù);
+) (hai góc kề bù).
Do đó .
Vì vậy đáp án C đúng.
• Xét ∆BAP và ∆CQA, có:
BA = CQ (giả thiết),
(chứng minh trên),
BP = AC (giả thiết)
Do đó ∆BAP = ∆CQA (c.g.c)
Vì vậy đáp án B đúng.
• Ta có ∆BAP = ∆CQA (chứng minh trên).
Suy ra AP = AQ và (cặp cạnh và cặp góc tương ứng).
∆APQ có
(do ∆PAM vuông tại M).
Suy ra ∆APQ vuông tại A.
Mà AP = AQ (chứng minh trên).
Do đó ∆APQ vuông cân tại A.
Vì vậy đáp án A đúng.
Câu 26. Cho ∆ABC vuông cân tại A. Trên cạnh AB lấy điểm D bất kì (D ≠ A, B), trên tia đối của tia AC, lấy điểm E sao cho AD = AE. Khẳng định nào sau đây đúng nhất?
A. ;
B. CD ⊥ BE;
C. D là trực tâm của ∆BEC;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
• Xét ∆ABE và ∆ACD, có:
,
AE = AD (giả thiết),
AB = AC (do ∆ABC vuông cân tại A).
Do đó ∆ABE = ∆ACD (hai cạnh góc vuông)
Suy ra (cặp góc tương ứng).
Vì vậy đáp án A đúng.
• Gọi F là giao điểm của CD và BE.
Ta có (hai góc đối đỉnh).
Xét ∆ACD vuông tại A có: (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra .
∆DBF có: (định lí tổng ba góc của một tam giác)
Suy ra .
Do đó BF ⊥ FD hay BE ⊥ CD.
Do đó đáp án B đúng.
• Xét ∆BCE có BA, CD là hai đường cao.
Mà BA cắt CD tại D.
Suy ra D là trực tâm của ∆BCE.
Do đó đáp án C đúng.
Câu 27. Cho ∆ABC có AB < AC, lấy điểm E trên cạnh CA sao cho CE = BA. Các đường trung trực của các đoạn thẳng BE và CA cắt nhau tại I. Chọn khẳng định sai.
A. ∆AIB = ∆EIC;
B. AI là đường phân giác của ∆ABC;
C. ;
D. IA = IC.
Đáp án: A
Giải thích:
• Gọi M, N lần lượt là trung điểm BE, AC.
Vì IM là đường trung trực của đoạn thẳng BE nên IB = IE.
Vì IN là đường trung trực của đoạn thẳng AC nên IA = IC.
Do đó đáp án D đúng.
• Xét ∆AIB và ∆CIE, có:
IA = IC (chứng minh trên),
AB = CE (giả thiết),
IB = IE (chứng minh trên)
Do đó ∆AIB = ∆CIE (cạnh – cạnh – cạnh).
Vì vậy đáp án A sai do chưa đúng kí hiệu bằng nhau của hai tam giác.
•Ta có ∆AIB = ∆CIE (chứng minh trên).
Suy ra (cặp góc tương ứng).
Mà (do ∆IAC cân tại I).
Do đó .
Vì vậy đáp án C đúng.
•Ta có (chứng minh trên).
Suy ra AI là tia phân giác của .
Hay AI là đường phân giác của ∆ABC.
Do đó đáp án B đúng.
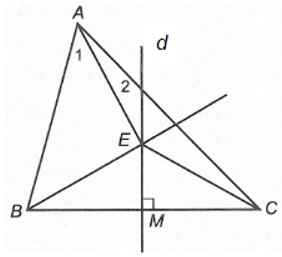
Câu 28. Cho ∆ABC có , . Vẽ đường trung trực d của cạnh BC và d cắt BC tại M. Gọi E là điểm thuộc d (E nằm bên trong ∆ABC) sao cho . Khẳng định nào sau đây đúng nhất?
A. ∆BEC cân tại E;
B. ;
C. ;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
+) ∆BEC có EM là đường trung trực của cạnh BC (giả thiết).
Ta suy ra EB = EC.
Do đó ∆BEC cân tại E.
Vì vậy đáp án A đúng.
+) Vì ∆BEC cân tại E nên .
Ta có:
Do đó đáp án B đúng.
+) Xét phương án C
• Nếu thì:
∆ABE có (định lí tổng ba góc trong một tam giác)
Suy ra .
Do đó (3).
Suy ra BE < AE (quan hệ giữa cạnh và góc đối diện)
Vì vậy EC < AE (∆BCE cân tại E).
Suy ra (4).
Từ (3), (4), ta suy ra .
Điều này vô lý vì .
Do đó ta loại trường hợp .
• Nếu thì:
Ta lập luận tương tự, ta được AE < EC và .
Điều này vô lý vì .
Do đó ta loại trường hợp .
Vì vậy .
Do đó đáp án C đúng.
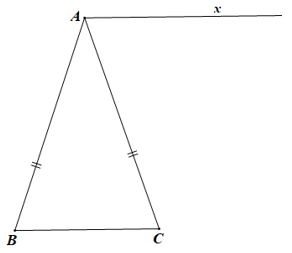
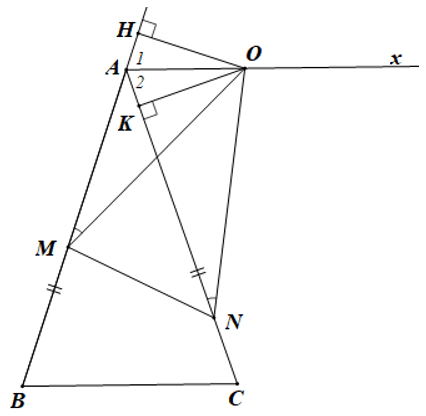
Câu 29. Cho ∆ABC cân tại A. Vẽ tia Ax // BC như hình bên.
Lấy điểm O trên tia Ax, điểm M trên AB và điểm N trên AC sao cho . Hỏi ∆OMN là tam giác gì?
A. Tam giác cân tại O;
B. Tam giác đều;
C. Tam giác cân tại M;
D. Tam giác vuông tại N.
Đáp án: A
Giải thích:
• Ta có Ax // BC nên (cặp góc đồng vị) và (cặp góc so le trong).
Mà (do ∆ABC cân tại A).
Suy ra .
• Kẻ OH ⊥ AB và OK ⊥ AC.
Xét ∆AHO và ∆AKO, có:
,
AO là cạnh chung,
(chứng minh trên),
Do đó ∆AHO = ∆AKO (cạnh huyền – góc nhọn).
Suy ra OH = OK (cặp cạnh tương ứng).
• ∆HOM vuông tại H: (1).
• ∆KON vuông tại K: (2).
Ta có (giả thiết) (3).
Từ (1), (2), (3), ta suy ra .
• Xét ∆HOM và ∆KON, có:
,
OH = OK (chứng minh trên),
(chứng minh trên),
Do đó ∆HOM = ∆KON (cạnh góc vuông – góc nhọn kề)
Suy ra OM = ON (cặp cạnh tương ứng).
Vì vậy ∆OMN cân tại O.
Câu 30. Cho ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA, lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khẳng định nào sau đây sai?
A. M là trọng tâm của ∆ABD;
B. DM đi qua trung điểm của AB;
C. ;
D. .
Đáp án: C
Giải thích:
•Ta có BM = 2MC.
Suy ra
Do đó
Hay
Suy ra (1).
Do đó đáp án D đúng.
• Vì ∆ABD có AC = CD nên C là trung điểm AD.
Do đó BC là đường trung tuyến của ∆ABD (2).
Từ (1), (2), ta suy ra M là trọng tâm của ∆ABD.
Do đó đáp án A đúng.
• Vì M là trọng tâm của ∆ABD nên DM đi qua trung điểm của cạnh AB.
Do đó đáp án B đúng.
• Vì M là trọng tâm của ∆ABD nên .
Do đó đáp án C sai.
Các câu hỏi trắc nghiệm Toán 7 sách Cánh diều có đáp án, chọn lọc khác: