Trắc nghiệm Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
Bộ 15 bài tập trắc nghiệm Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 4.
Trắc nghiệm Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh - Cánh diều
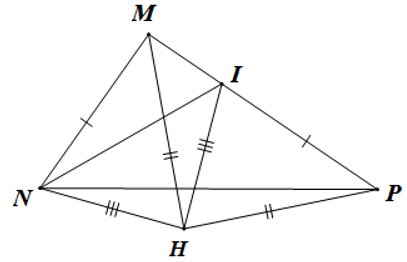
Câu 1. Cho tam giác MNP có MN < MP. Lấy điểm I trên cạnh MP sao cho MN = PI. Gọi H là điểm sao cho HM = HP, HN = HI.
Khẳng định nào sau đây là đúng?
A. ∆MNH = ∆PIH;
B. ∆MNH = ∆PHI;
C. ;
D. .
Đáp án: A
Giải thích:
Xét ∆MNH và ∆PIH ta có:
HM = HP (giả thiết);
HN = HI (giả thiết);
MN = PI (giả thiết).
Do đó ∆MNH = ∆PIH (c.c.c)
Suy ra (các cặp góc tương ứng)
Vậy ta chọn phương án A.
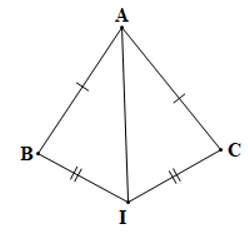
Câu 2. Xét bài toán “∆IAB và ∆IAC có AB = AC, IB = IC (điểm I nằm ngoài tam giác ABC). Chứng minh rằng .”
Cho các câu sau:
(1) “AB = AC (giả thiết),
IB = IC (giả thiết),
IA là cạnh chung”;
(2) “Suy ra ∆IAB = ∆IAC (c.c.c)”;
(3) “Do đó (hai góc tương ứng)”;
(4) “Xét ∆IAB và ∆IAC có:”.
Hãy sắp xếp một cách hợp lí các câu trên để giải bài toán.
A. (2), (4), (1); (3);
B. (4), (2), (1), (3);
C. (1), (2), (3), (4);
D. (4), (1), (2), (3).
Đáp án: D
Giải thích:
Ta đi chứng minh như sau:
Xét ∆IAB và ∆IAC có:
AB = AC (giả thiết),
IB = IC (giả thiết),
IA là cạnh chung;
Suy ra ∆IAB = ∆IAC (c.c.c);
Do đó (hai góc tương ứng).
Vậy ta chọn phương án D.
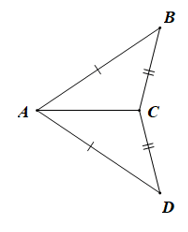
Câu 3. Cho hình vẽ sau:
Khẳng định nào sau đây là đúng?
A. ∆ABC = ∆ADC;
B. ∆ABC = ∆ACD;
C. ∆ACB = ∆ADC;
D. ∆BCA = ∆DAC.
Đáp án: A
Giải thích:
Xét tam giác ABC và tam giác CDA có:
AB = AD, BC = DC, AC là cạnh chung
Suy ra ∆ABC = ∆ADC (c.c.c)
Vậy ∆ABC = ∆ADC hay ta có thể kí hiệu ∆ACB = ∆ACD hoặc ∆BCA = ∆DCA.
Vậy ta chọn phương án A.
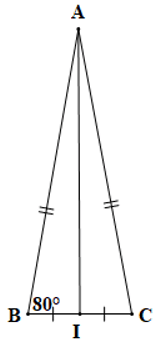
Câu 4. Cho tam giác ABC có AB = AC, I là trung điểm của BC. Biết , số đo của là:
A. 40°;
B. 30°;
C. 20°;
D. 10°.
Đáp án: D
Giải thích:
Xét tam giác ABI và tam giác ACI có:
AB = AC (giả thiết),
IB = IC (do I là trung điểm của BC),
AI là cạnh chung
Do đó ∆ABI = ∆ACI (c.c.c)
Suy ra (các cặp góc tương ứng)
Mà nên
Ta có: (hai góc kề bù)
Nên
Do đó tam giác ACI vuông tại I
Khi đó (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra
Vậy ta chọn phương án D.
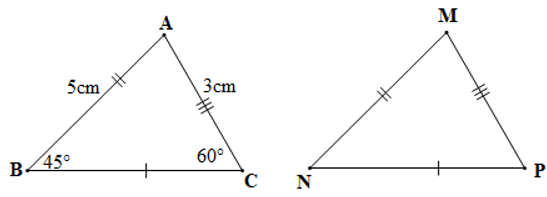
Câu 5. Cho hình vẽ bên dưới:
Số đo góc M và độ dài cạnh MN lần lượt là:
A. MN = 5 cm;
B. MN = 3 cm;
C. MN = 5 cm;
D. MN = 3 cm.
Đáp án: C
Giải thích:
Xét tam giác ABC và tam giác MNP có:
AB = MN, BC = NP, AC = MP (giả thiết)
Suy ra ∆ABC = ∆MNP (c.c.c)
Do đó MN = BA = 5 cm (hai cạnh tương ứng) và (hai góc tương ứng)
Xét tam giác BCA có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Do đó
Vậy và MN = 5 cm.
Vậy ta chọn phương án C.
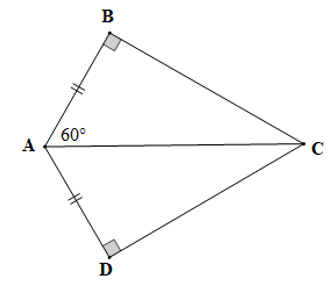
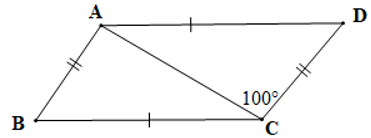
Câu 6. Cho hình vẽ bên dưới:
Biết AB=AD, . Số đo góc ACD là:
A. 20°;
B. 30°;
C. 40°;
D. 60°.
Đáp án: B
Giải thích:
Xét ∆ABC và ∆ADC có:
AB = AD (giả thiết),
AC là cạnh chung
Do đó ∆ABC = ∆ADC (cạnh huyền – cạnh góc vuông)
Suy ra (cặp góc tương ứng)
Xét ∆ABC vuông tại B có: (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra
Mà (chứng minh trên)
Do đó
Vậy số đo góc ACD là 30°.
Vậy ta chọn phương án B.
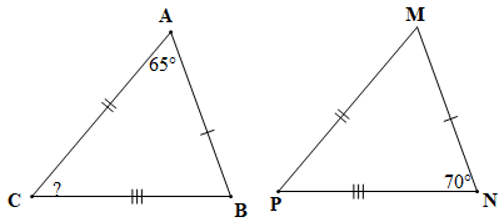
Câu 7. Cho hình vẽ bên dưới:
Số đo góc C và góc M lần lượt là:
A. 45° và 65°;
B. 65° và 45°;
C. 55° và 70°;
D. 70° và 55°.
Đáp án: A
Giải thích:
Xét tam giác ABC và tam giác MNP có:
AB = MN, BC = NP, AC = MP (giả thiết)
Suy ra ∆ABC = ∆MNP (c.c.c)
Do đó (các cặp góc tương ứng)
Mà , nên
Xét tam giác ABC có: (tổng ba góc trong một tam giác)
Suy ra
Hay
Vậy số đo góc C và góc M lần lượt là: 45° và 65°.
Vậy ta chọn phương án A.
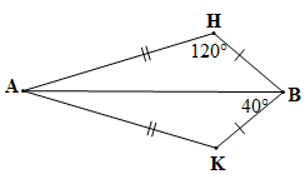
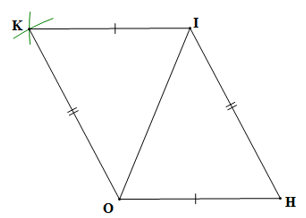
Câu 8. Cho hình vẽ bên dưới:
Số đo của trong hình vẽ trên bằng:
A. 50°;
B. 40°;
C. 30°;
D. 20°.
Đáp án: D
Giải thích:
Xét tam giác ABH và tam giác ABK có:
AH = AK, BH = BK, AB là cạnh chung
Suy ra ∆ABH = ∆ABK (c.c.c)
Do đó (cặp góc tương ứng)
Mà nên
Xét tam giác ABK có: (tổng ba góc trong một tam giác)
Suy ra
Hay
Vậy số đo của bằng 20°.
Vậy ta chọn phương án D.
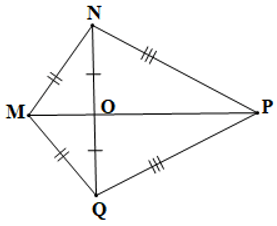
Câu 9. Cho hình vẽ bên dưới:
Số cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh là:
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
+) Xét ∆MNP và ∆MQP có:
MN = MQ, NP = QP, MP là cạnh chung
Suy ra ∆MNP = ∆MQP (c.c.c)
+) Xét ∆NPO và ∆QPO có:
NP = QP, NO = QO, PO là cạnh chung
Suy ra ∆NPO = ∆QPO (c.c.c)
+) Xét ∆MNO và ∆MQO có:
MN = MQ, NO = QO, MO là cạnh chung
Suy ra ∆MNO = ∆MQO (c.c.c)
Vậy trong hình vẽ trên có 3 cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh.
Vậy ta chọn phương án C.
Câu 10. Cho hình vẽ bên dưới:
Khẳng định nào sau đây là sai?
A. và AD // BC;
B. và AD không song song với BC;
C. và AB // DC;
D. ∆ABC = ∆CDA.
Đáp án: B
Giải thích:
• Xét ∆ABC và ∆ACD có:
AB = CD, BC = DA, AC là cạnh chung
Suy ra ∆ABC = ∆CDA (c.c.c)
Do đó phương án D là đúng.
• Vì ∆ABC = ∆CDA (chứng minh trên)
Nên (hai góc tương ứng)
Mà
Nên
Mặt khác: ∆ABC = ∆CDA (chứng minh trên)
Suy ra (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Do đó AD // BC (dấu hiệu nhận biết).
Vậy A là đúng
•Ta có (chứng minh trên)
Mà hai góc này ở vị trí so le trong
Do đó AB // DC (dấu hiệu nhận biết). Vậy C là đúng
Vậy ta chọn đáp án B.
Câu 11. Cho tam giác IOH, vẽ cung tròn tâm I bán kính OH, vẽ cung tròn tâm O bán kính IH, hai cung tròn này cắt nhau tại K (K và H nằm khác phía so với đường thẳng IO). Khẳng định nào sau đây là đúng nhất?
A. HO // KI;
B. OK // IH;
C. Cả A và B đều sai;
D. Cả A và B đều đúng.
Đáp án: D
Giải thích:
Xét ∆IOH và ∆IOK có:
KO = IH (K nằm trên cung tròn tâm O bán kính IH),
OH = IK (K nằm trên cung tròn tâm I bán kính OH),
IO là cạnh chung
Do đó ∆IOH = ∆OIK (c.c.c)
Suy ra (các cặp góc tương ứng)
Mà và ở vị trí so le trong của IK và OH nên IK // OH (dấu hiệu nhận biết)
và ở vị trí so le trong của KO và IH nên KO // IH (dấu hiệu nhận biết)
Vậy ta chọn phương án D.
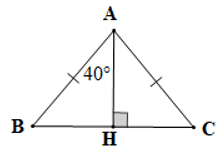
Câu 12. Cho hình vẽ sau:
Số đo của trong hình vẽ trên bằng:
A. 20°;
B. 40°;
C. 80°;
D. 120°.
Đáp án: C
Giải thích:
Vì AHBCnên
Xét ∆ABH và ∆ACH có:
(chứng minh trên),
AB = AC (giả thiết),
AH là cạnh chung
Do đó ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông)
Suy ra (cặp góc tương ứng)
Mà nên
Ta có
Suy ra
Vậy số đo góc BAC là 80°.
Vậy ta chọn phương án C.
Câu 13. Cho hai tam giác MNP và OHK có MN = OH, NP = HK. Điều kiện để ∆NMP = ∆HOK theo trường hợp cạnh – cạnh – cạnh là:
A. MP = OH;
B. MN = KH;
C. MP = OK;
D. Không có điều kiện nào thoả mãn.
Đáp án: C
Giải thích:
Vì ∆NMP = ∆HOK theo trường hợp cạnh – cạnh – cạnh mà MN = OH, NP = HK
Nên điều kiện còn thiếu là MP = OK.
Vậy ta chọn phương án C.
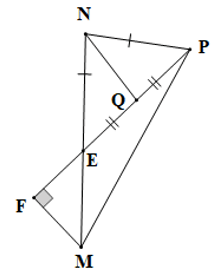
Câu 14. Cho tam giác NMP (NP < MN). Trên cạnh MN lấy điểm E sao cho NE = NP. Lấy Q là trung điểm của PE. Qua M kẻ đường thẳng vuông góc với PE tại F. Chọn khẳng định đúng:
A.
B. FM // NQ;
C. ∆ENQ = ∆PQN;
D. Cả A, B, C đều đúng.
Đáp án: B
Giải thích:
• Xét ∆ENQ và ∆PQN có:
NE = NP (giả thiết),
QE = QP (do Q là trung điểm của PE),
NQ là cạnh chung
Suy ra ∆ENQ = ∆PNQ (c.c.c)
Do đó phương án C là sai.
• Vì ∆ENQ = ∆PNQ (chứng minh trên)
Suy ra (các cặp góc tương ứng)
Mà (hai góc kề bù)
Nên
Do đó NQ PE. Vậy đáp án A là sai
Mà FM PE (giả thiết), nên FM // NQ , vậy đáp án B là đúng
Vậy ta chọn phương án B.
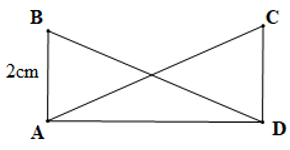
Câu 15. Cho hình vẽ:
Biết , AC = BD. Độ dài cạnh CD là:
A. 4 cm;
B. 5 cm;
C. 2 cm;
D. 3 cm.
Đáp án: C
Giải thích:
Xét ∆ABD và ∆ACD có:
(giả thiết),
AC = BD (giả thiết),
AD là cạnh chung
Do đó ∆ABD = ∆DCA (cạnh huyền – cạnh góc vuông)
Suy ra AB = CD (cặp cạnh tương ứng)
Mà AB = 2 cm nên CD = 2 cm.
Vậy độ dài cạnh CD là 2 cm.
Vậy ta chọn phương án C.
Các câu hỏi trắc nghiệm Toán 7 sách Cánh diều có đáp án, chọn lọc khác: