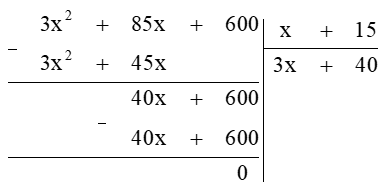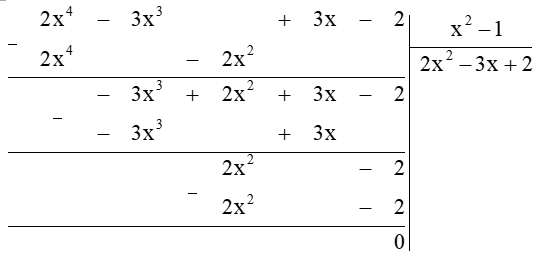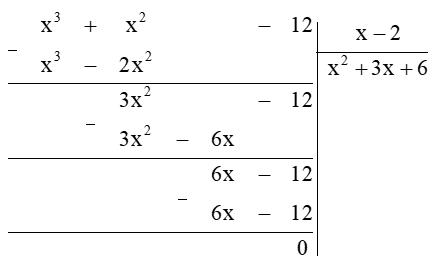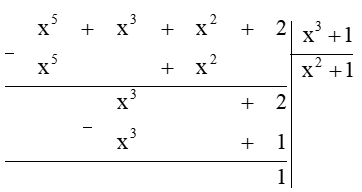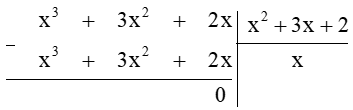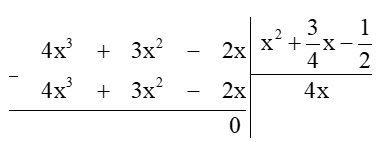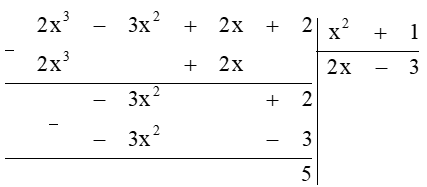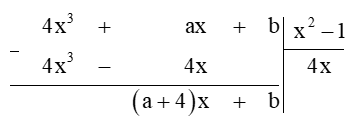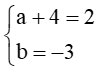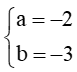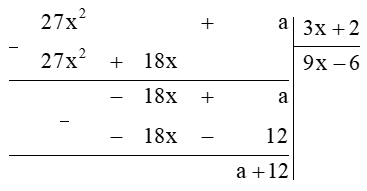Trắc nghiệm Toán 7 Bài 5: Phép chia đa thức một biến
Bộ 15 bài tập trắc nghiệm Toán 7 Bài 5: Phép chia đa thức một biến có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 5.
Trắc nghiệm Toán 7 Bài 5: Phép chia đa thức một biến - Cánh diều
Câu 1. Một công ty sau khi tăng giá 15 nghìn đồng mỗi sản phẩm so với giá ban đầu là x (nghìn đồng) thì có doanh thu là 3x2 + 85x + 600 nghìn đồng. Tính số sản phẩm mà công ty đó đã bán được theo x.
A. 3x – 40;
B. 3x + 40;
C. –3x – 40;
D. –3x + 40.
Đáp án: B
Giải thích:
Giá của sản phẩm sau khi tăng là: x + 15 (nghìn đồng)
Số sản phẩm mà công ty đó bán được là thương của phép chia:
(3x2 + 85x + 600) : (x + 15)
Thực hiện đặt tính chia đa thức như sau:
Do đó (3x2 + 85x + 600) : (x + 15) = 3x + 40.
Vậy công ty đó bán được 3x + 40 sản phẩm.
Câu 2. Tính (12x4) : (3x2)
A. 4x;
B. 4x2;
C. –4x;
D. –4x2.
Đáp án: B
Giải thích:
Ta có: (12x4) : (3x2)
= (12 : 3). (x4 : x2)
= 4x4 – 2
= 4x2.
Vậy (12x4) : (3x2) = 4x2.
Câu 3. Kết quả của phép tính (với m, n ∈ ℕ) là:
A.
B.
C.
D.
Đáp án: A
Giải thích:
Ta có:
Vậy ta chọn phương án A.
Câu 4. Kết quả của phép tính (18x6 + 6x4 – 3x2) : (3x2) là
A. 6x4 + 2x2 + 1;
B. 6x4 – 2x2 + 1;
C. 6x4 + 2x2 – 1;
D. 6x4 – 2x2 – 1.
Đáp án: C
Giải thích:
Ta có: (18x6 + 6x4 – 3x2) : (3x2)
= (18x6) : (3x2) + (6x4) : (3x2) – (3x2) : (3x2)
= (18 : 3). (x6 : x2) + (6 : 3). (x4 : x2) – (3 : 3). (x2 : x2)
= 6x4 + 2x2 – 1.
Vậy (18x6 + 6x4 – 3x2) : (3x2) = 6x4 + 2x2 – 1.
Vậy ta chọn phương án C.
Câu 5. Kết quả của phép chia 0,5x5 + 3,2x3 – 2x2 cho 0,25xn, với n = 2.
A. 2x3 + 12,8x + 8;
B. 2x3 + 12,8x – 8;
C. 2x3 – 12,8x – 8;
D. 2x3 – 12,8x – 8.
Đáp án: B
Giải thích:
Thay n = 2 vào 0,25xn ta được biểu thức 0,25x2.
Khi đó
(0,5x5 + 3,2x3 – 2x2) : (0,25x2)
= (0,5x5) : (0,25x2) + (3,2x3) : (0,25x2) – (2x2) : (0,25x2)
= (0,5 : 0,25). (x5 : x2) + (3,2 : 0,25). (x3 : x2) – (2 : 0,25). (x2 : x2)
= 2x3 + 12,8x – 8
Vậy (0,5x5 + 3,2x3 – 2x2) : (0,25xn) = 2x3 + 12,8x – 8 với n = 2.
Câu 6. Phép chia đa thức 2x4 – 3x3 + 3x – 2 cho đa thức x2 – 1 được đa thức dư là
A. 0;
B. 1;
C. 2;
D. 10.
Đáp án: A
Giải thích:
Ta thực hiện đặt tính chia đa thức:
Vậy đa thức dư là R = 0.
Câu 7. Điền vào chỗ trống (x3 + x2 – 12 : (x – 12) = …
A. x + 3;
B. x – 3;
C. x2 + 3x + 6;
D. x2 – 3x + 6.
Đáp án: C
Giải thích:
Ta thực hiện đặt tính chia đa thức:
Do đó (x3 + x2 – 12 : (x – 12) = x2 + 3x + 6.
Vậy đa thức cần điền vào chỗ trống là x2 + 3x + 6.
Câu 8. Biết phần dư của phép chia đa thức (x5 + x3 + x2 + 2) cho đa thức (x3 + 1) là số tự nhiên a. Chọn câu đúng.
A. a < 2;
B. a > 1;
C. a < 0;
D. a ⁝ 2.
Đáp án: A
Giải thích:
Ta thực hiện đặt tính chia đa thức:
Phần dư của phép chia là a = 1 < 2.
Vậy ta chọn phương án A.
Câu 9. Tìm đa thức bị chia biết đa thức chia là (x2 + x + 1), thương là (x + 3), dư là x – 2.
A. x3 + 4x2 + 5x + 1;
B. x3 – 4x2 + 5x + 1;
C. x3 – 4x2 – 5x + 1;
D. x3 + 4x2 – 5x + 1.
Đáp án: A
Giải thích:
Đa thức bị chia cần tìm là:
(x2 + x + 1)(x + 3) + x – 2
= x2.x + 3x2 + x.x + 3x + x + 3 + x – 2
= x3 + 3x2 + x2 + 3x + x + x + 3 – 2
= x3 + 4x2 + 5x + 1
Vậy đa thức cần tìm là x3 + 4x2 + 5x + 1.
Câu 10. Một hình hộp chữ nhật có thể tích là x3 + 3x2 + 2x (cm3). Biết đáy là hình chữ nhật có các kích thước là x + 1 (cm) và x + 2 (cm). Tính chiều cao của hình hộp chữ nhật đó.
A. x (cm);
B. 2x (cm);
C. 3x (cm);
D. 4x (cm).
Đáp án: A
Giải thích:
Ta có V = Sđáy. h
Diện tích đáy của hình hộp chữ nhật là:
(x + 1)(x + 2)
= x.x + x.2 + 1.x + 1.2
= x2 + 3x + 2 (cm2)
Chiều cao của hình hộp chữ nhật đó là thương của phép chia:
(x3 + 3x2 + 2x) : (x2 + 3x + 2)
Ta đặt tính phép chia đa thức:
Do đó (x3 + 3x2 + 2x) : (x2 + 3x + 2) = x
Vậy chiều cao của hình hộp chữ nhật đó là x (cm).
Câu 11. Rút gọn và tính giá trị biểu thức tại x = 3.
A. A = 4x, A = 7;
B. A = 3x; A = 9;
C. A = 4x; A = 8;
D. A = 4x; A = 12.
Đáp án: D
Giải thích:
Ta thực hiện đặt tính chia đa thức như sau:
Do đó A = 4x.
Tại x = 3, ta có: A = 4.3 = 12.
Vậy ta chọn phương án D.
Câu 12. Với a ≠ 0, b ≠ 0; m, n ∈ N; m ≥ n; kết quả của phép tính (axm) : (bxn) bằng:
A. . xm – n;
B. . xm + n;
C. . xm.n;
D. . xm – n.
Đáp án: A
Giải thích:
Với a ≠ 0, b ≠ 0; m, n ∈ N; m ≥ n, ta có:
(axm) : (bxn) = . (xm : xn) = . xm – n
Vậy ta chọn phương án A.
Câu 13. Có bao nhiêu số nguyên x để giá trị của đa thức A = 2x3 – 3x2 + 2x + 2 chia hết cho giá trị của đa thức B = x2 + 1
A. 3;
B. 4;
C. 2;
D. 1.
Đáp án: A
Giải thích:
Ta thực hiện đặt tính chia đa thức như sau:
Để giá trị của đa thức A = 2x3 – 3x2 + 2x + 2 chia hết cho giá trị của đa thức B = x2 + 1 thì 5 ⁝ (x2 + 1)
Hay (x2 + 1) ∈ Ư(5) = {–1; 1; –5; 5}
+) x2 + 1 = –1
Suy ra x2 = –2 (vô lí)
+) x2 + 1 = 1
Suy ra x2 = 0
Do đó x = 0 (thỏa mãn x là số nguyên)
+) x2 + 1 = –5
Suy ra x2 = –6 (vô lí)
+) x2 + 1 = 5
Suy ra x2 = 4
Do đó x = 2 (thỏa mãn) hoặc x = –2 (thỏa mãn)
Vậy có 3 giá trị của x thỏa mãn đề bài là x = 0; x = –2; x = 2.
Ta chọn phương án A.
Câu 14. Tìm giá trị của a và b đề đa thức 4x3 + ax + b chia cho đa thức x2 – 1 dư 2x – 3.
A. a = –6; b = –3;
B. a = 6; b = –3;
C. a = 2; b = –3;
D. a = –2; b = –3.
Đáp án: D
Giải thích:
Ta đặt tính chia đa thức như sau:
Phần dư của phép chia trên là (a + 4)x + b.
Mà theo bài, đa thức 4x3 + ax + b chia cho đa thức x2 – 1 dư 2x – 3.
Do đó (a + 4)x + b = 2x – 3.
Suy ra
Hay
Vậy a = –2 và b = –3.
Ta chọn phương án D.
Câu 15. Xác định a để đa thức 27x2 + a chia hết cho 3x + 2
A. a = 6;
B. a = 12;
C. a = –12;
D. a = 9.
Đáp án: C
Giải thích:
Ta thực hiện đặt tính chia đa thức như sau:
Suy ra 27x2 + a = (3x + 2).(9x – 6) + a + 12
Để phép chia trên là phép chia hết thì R = a + 12 = 0.
Do đó a = –12.
Vậy ta chọn phương án C.
Các câu hỏi trắc nghiệm Toán 7 sách Cánh diều có đáp án, chọn lọc khác: