Trắc nghiệm Toán 7 Bài 3: Phép cộng, phép trừ đa thức một biến
Bộ 15 bài tập trắc nghiệm Toán 7 Bài 3: Phép cộng, phép trừ đa thức một biến có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 3.
Trắc nghiệm Toán 7 Bài 3: Phép cộng, phép trừ đa thức một biến - Cánh diều
Câu 1. A(x) = 5x4 + 4x3 + 2x + 1 và B(x) = –5x4 + x3 + 3x2 + x – 1. Bậc của đa thức N(x) = A(x) + B(x) là:
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
Ta có: N(x) = A(x) – B(x)
= (5x4 + 4x3 + 2x + 1) + (–5x4 + x3 + 3x2 + x – 1)
= 5x4 + 4x3 + 2x + 1 – 5x4 + x3 + 3x2 + x – 1
= (5x4 – 5x4) + (4x3 + x3) + 3x2 + (2x + x) + (1 – 1)
= 5x3 + 3x2 + 3x.
Do đó N(x) = 5x3 + 3x2 + 3x.
Vậy bậc của đa thức N(x) là 3.
Ta chọn phương án C.
Câu 2. Cho hai đa thức f(x) = x2 + 3x – 5 và g(x) = –5x2 – x + 2.
Tính k(x) = f(x) –g(x) và tìm bậc củak(x).
A. k(x) = 6x2 + 4x – 7 và bậc của k(x) là 2;
B. h(x) = –4x2 + 2x – 3 và bậc của k(x) là 2;
C. k(x) = 6x2 + 4x – 7 và bậc của k(x) là 6;
D. k(x) = –4x2 + 2x – 3 và bậc của k(x) là 4.
Đáp án: A
Giải thích:
Ta có: k(x) = f(x) – g(x)
= (x2 + 3x – 5) – (–5x2 – x + 2)
= x2 + 3x – 5 + 5x2 + x – 2
= (x2 + 5x2) + (3x + x) + (–5 – 2)
= 6x2 + 4x – 7
Vậy k(x) = 6x2 + 4x – 7 và bậc của k(x) là 2.
Câu 3. Cho f(x) = 3x5 – 3x4 + x2 – 5 và g(x) = 2x4 – x3 – x2 + 5.
Tính hiệu f(x) – g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
A. 10 + 2x2 + x3 – 5x4 + 3x5;
B. –10 + 2x2 + x3 – 5x4 + 3x5;
C. 3x5 – 5x4 + x3 + 2x2 + 10;
D. 3x5 – 5x4 + x3 + 2x2 – 10.
Đáp án: B
Giải thích:
Ta có:
f(x) – g(x)
= (3x5 – 3x4 + x2 – 5) – (2x4 – x3 – x2 + 5)
= 3x5 – 3x4 + x2 – 5 – 2x4 + x3 + x2 – 5
= 3x5 + (–3x4 – 2x4) + x3 + (x2 + x2) – 5 – 5
= 3x5 – 5x4 + x3 + 2x2 – 10
Sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
f(x) – g(x) = –10 + 2x2 + x3 – 5x4 + 3x5.
Vậy ta chọn phương án B.
Câu 4. Cho P(x) = 3x4 + 4x3 – 3x2 + 2x – 1 và Q(x) = –x4 + 2x3 – 3x2 + 4x – 5.
Tính P(x) + Q(x) rồi tìm bậc của đa thức thu gọn.
A. P(x) + Q(x) = 6x3 – 6x2 + 6x – 6 có bậc là 3;
B. P(x) + Q(x) = 2x4 + 6x3 – 6x2 + 6x + 6 có bậc là 4;
C. P(x) + Q(x) = 2x4 + 6x3 – 6x2 + 6x – 6 có bậc là 4;
D. P(x) + Q(x) = 2x4 + 6x3 + 6x – 6 có bậc là 4.
Đáp án: C
Giải thích:
Ta có:
P(x) + Q(x)
= (3x4 + 4x3 – 3x2 + 2x – 1) + (–x4 + 2x3 – 3x2 + 4x – 5)
= 3x4 + 4x3 – 3x2 + 2x – 1 – x4 + 2x3 – 3x2 + 4x – 5
= (3x4 – x4) + (4x3 + 2x3) + (–3x2 – 3x2) + (2x + 4x) – 1 – 5
= 2x4 + 6x3 – 6x2 + 6x – 6.
Bậc của đa thức P(x) + Q(x) = 2x4 + 6x3 – 6x2 + 6x – 6 là 4.
Vậy ta chọn phương án C.
Câu 5. Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = 5x4 – 4x2 + 6x3 + x – 1; g(x) = 3 – 2x.
A. –1;
B. –5;
C. 4;
D. 6.
Đáp án: B
Giải thích:
Ta có: f(x) + k(x) = g(x)
Suy ra k(x) = g(x) – f(x)
= 3 – 2x – (5x4 – 4x2 + 6x3 + x – 1)
= 3 – 2x – 5x4 + 4x2 – 6x3 – x + 1
= –5x4 – 6x3 + 4x2 + (–2x – x) + 3 + 1
= –5x4 – 6x3 + 4x2 – 3x + 4
Nhận thấy số hạng có lũy thừa cao nhất của biến là –5x4 nên hệ số cao nhất là –5.
Vậy ta chọn phương án B.
Câu 6. Cho đa thức P(x) = –6x5 – 4x4 + 3x2 – 2x và Q(x) = 2x5 – 4x4 – 2x3 + 2x2 – x – 3. Tính M(1) với M(x) = P(x) – Q(x).
A. –3;
B. 3;
C. –2;
D. 2.
Đáp án: A
Giải thích:
Ta có: M(x) = P(x) – Q(x)
M(x) = P(x) – Q(x)
= (–6x5 – 4x4 + 3x2 – 2x) – (2x5 – 4x4 – 2x3 + 2x2 – x – 3)
= –6x5 – 4x4 + 3x2 – 2x – 2x5 + 4x4 + 2x3 – 2x2 + x + 3
= (–6x5 – 2x5) + (–4x4 + 4x4) + 2x3 + (3x2 – 2x2) + (–2x + x) + 3
= –8x5 + 2x3 + x2 – x + 3
Nên M(x) = –8x5 + 2x3 + x2 – x + 3
Thay x = 1 vào M(x) ta được:
M(1) = –8.15 + 2.13 + 12 – 1 + 3
= –8.1 + 2.1 + 1 – 1 + 3
= –8 + 2 + 3
= –3
Vậy ta chọn phương án A.
Câu 7. Cho A(x) = 5x3 – 4x2 + 3x + 3; B(x) = 4 – x – 4x2 + 5x3. Giá trị nào của x sau đây là thỏa mãn C(x) = 7 biết C(x) = A(x) – B(x)?
A. x = 2;
B. x = –2;
C. x = 1;
D. x = –1.
Đáp án: A
Giải thích:
Ta có:
C(x) = A(x) – B(x)
= (5x3 – 4x2 + 3x + 3) – (4 – x – 4x2 + 5x3)
= 5x3 – 4x2 + 3x + 3 – 4 + x + 4x2 – 5x3
= (5x3 – 5x3) + (–4x2 + 4x2) + (3x + x) + (3 – 4)
= 4x – 1
Lại có: C(x) = 7
Suy ra 4x – 1 = 7
Hay 4x = 8.
Do đó x = 2.
Vậy ta chọn phương án A.
Câu 8. Cho hai đa thức P(x) và Q(x) dưới đây, hai đa thức nào thỏa mãn P(x) – Q(x) = 2x – 2 là:
A. P(x) = x2 – 2x; Q(x) = –2x – 2;
B. P(x) = x2 – 2x; Q(x) = 2x2 + 2x;
C. P(x) = 2x; Q(x) = –2;
D. P(x) = x3 – 2; Q(x) = x3 – 2x.
Đáp án: D
Giải thích:
Theo đề bài ta có: P(x) – Q(x) = 2x – 2
• Xét phương án A với P(x) = x2 – 2x; Q(x) = –2x – 2 thì
P(x) – Q(x)
= x2 – 2x – (–2x – 2)
= x2 – 2x + 2x + 2
= x2 + (–2x + 2x) + 2
= x2 + 2
Đa thức này khác đa thức 2x – 2, do đó A không thoả mãn yêu cầu.
• Xét phương án B với P(x) = 2x2 - 2; Q(x) = 2x2 + 2x thì
P(x) – Q(x)
= 2x2 – 2 – (2x2 + 2x)
= 2x2 – 2 – 2x2 – 2x
= (2x2 – 2x2) – 2x – 2
= –2x – 2
Đa thức này khác đa thức 2x – 2, do đó B không thoả mãn yêu cầu.
• Xét phương đáp án C với P(x) = 2x; Q(x) = –2 thì
P(x) – Q(x)
= 2x – (– 2)
= 2x + 2
Đa thức này khác đa thức 2x – 2, do đó C không thỏa mãn yêu cầu bài toán.
• Xét phương án D với P(x) = x3 – 2; Q(x) = x3 – 2x thì
P(x) – Q(x)
= x3 – 2 – (x3 – 2x)
= x3 – 2 – x3 + 2x
= 2x – 2
Do đó D thỏa mãn yêu cầu bài toán.
Vậy ta chọn phương án D.
Câu 9. Cho f(x) = 2x4 – 4x2 + 6x3 + 2x + 3; g(x) = x + 3 và f(x) + k(x) = g(x). Hệ số tự do của đa thức k(x) là:
A. –1;
B. 4;
C. 0;
D. 6.
Đáp án: C
Giải thích:
Ta có f(x) + k(x) = g(x)
Suy ra k(x) = g(x) – f(x)
= x + 3 – (2x4 – 4x2 + 6x3 + 2x + 3)
= x + 3 – 2x4 + 4x2 – 6x3 – 2x – 3
= –2x4 – 6x3 + 4x2 + (x – 2x) + 3 – 3
= –2x4 – 6x3 + 4x2 – x
Vậy hệ số tự do của k(x) là 0.
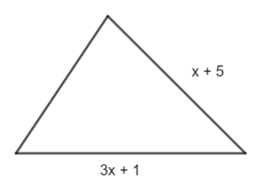
Câu 10. Cho tam giác như hình vẽ dưới đây, có chu vi bằng 6x – 10.
Độ dài cạnh chưa biết của tam giác trên là:
A. 2x + 17;
B. 2x – 17;
C. 17x + 2;
D. 17x – 2.
Đáp án: B
Giải thích:
Gọi cạnh cần tìm là P(x).
Ta có chu vi tam giác được tính bằng:
(x + 5) + (3x + 1) + P(x)
= (x + 3x) + (6 + 1) + P(x)
= 4x + 7 + P(x)
Mà theo bài chu vi tam giác là 6x – 10
Do đó 4x + 7 + P(x) = 6x – 10
Khi đó:
P(x) = 6x – 10 – (4x + 7)
= 6x – 10 – 4x – 7
= (6x – 4x) – (10 + 7)
= 2x – 17
Vậy cạnh cần tìm có độ dài là 2x – 17.
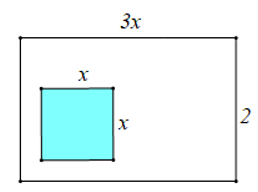
Câu 11. Một mảnh đất hình chữ nhật có kích thước chiều dài, chiều rộng lần lượt là 3x m và 2 m. Người ta dự định trồng hoa trong phần đất hình vuông có cạnh là x m như hình vẽ.
Diện tích phần đất còn lại (phần đất không tô màu) là:
A. x2 – 6x (m2);
B. 5x2 (m2);
C. 6x2 (m2);
D. 6x – x2 (m2).
Đáp án: D
Giải thích:
Diện tích mảnh đất hình chữ nhật là:
3x.2 = 6x (m2)
Diện tích phần đất trồng hoa là:
x.x = x2 (m2)
Diện tích phần đất còn lại (phần đất không tô màu) là:
6x – x2 (m2)
Vậy ta chọn phương án D.
Câu 12. Cho hai đa thức f(x) = 6x2 + 4x – 5 và g(x) = –6x2 – 4x + 2.
Tính h(x) = f(x) + g(x) và tìm bậc củah(x).
A. h(x) = 12x2 + 8x – 7 và bậc của h(x) là 2;
B. h(x) = –3 và bậc của h(x) là 1;
C. h(x) = 8x – 3 và bậc của h(x) là 1;
D. h(x) = –3 và bậc của h(x) là 0.
Đáp án: D
Giải thích:
Ta có: h(x) = f(x) + g(x)
= (6x2 + 4x – 5) + (–6x2 – 4x + 2)
= 6x2 + 4x – 5 – 6x2 – 4x + 2
= (6x2 – 6x2) + (4x – 4x) + (–5 + 2)
= –3
Vậy h(x) = –3 và bậc của h(x) là 0.
Câu 13. Bạn Minh nói: Tổng của hai đa thức bậc ba luôn là đa thức bậc ba.
Bạn Quân nói: Hiệu của hai đa thức bậc ba luôn là đa thức bậc ba.
Bạn Nam nói: Tổng của hai đa thức bậc ba chưa chắc là đa thức bậc ba.
Chọn khẳng định đúng.
A. Quân nói đúng;
B. Minh nói đúng;
C. Nam nói đúng;
D. Cả 3 bạn đều nói đúng.
Đáp án: C
Giải thích:
• Ta lấy ví dụ:
Cho hai đa thức bậc ba A(x) = –x3 + 2x + 1 và B(x) = x3 + 3
Ta thấy:
A(x) + B(x)
= –x3 + 2x + 1 + x3 + 3
= (–x3 + x3) + 2x + (1 + 3)
= 2x + 4
Đa thức này không phải là đa thức bậc ba nên Minh nói không đúng.
Từ đó ta thấy tổng của hai đa thức bậc ba chưa chắc là đa thức bậc ba nên Nam nói đúng.
• Ta có ví dụ: P(x) = –2x3 + x2 + 5x và Q(x) = –2x3 + 4x2 + 2x + 3
Ta thấy:
P(x) – Q(x)
= –2x3 + x2 + 5x – (–2x3 + 4x2 + 2x + 3)
= –2x3 + x2 + 5x + 2x3 – 4x2 – 2x – 3
= (–2x3 + 2x3) + (x2 – 4x2) + (5x – 2x) – 3
= –3x2 + 3x – 3
Đa thức này không phải là đa thức bậc ba nên Quân nói chưa đúng.
Vậy ta chọn phương án C.
Câu 14. Xác định P(x) = ax2 + bx + c biết P(1) = 0; P(–1) = 6 và P(2) = 3
A. P(x) = 3x – 3;
B. P(x) = –2x2 – 3x + 5;
C. P(x) = 2x2 – 3x + 1;
D. P(x) = 2x2 – 3x – 1.
Đáp án: C
Giải thích:
• Thay x = 1 vào P(x) = ax 2 + bx + c ta được:
P(1) = a. 12 + b.1 + c
= a + b + c
Mà P(1) = 0 nên a + b + c = 0
Suy ra a + c = –b (1)
• Thay x = –1 vào P(x) = ax 2 + bx + c ta được:
P(–1) = a.(–1)2 + b.(–1) + c
= a – b + c
Mà P (–1) = 6 nên a – b + c = 6
Suy ra a + c = 6 + b (2)
• Thay x = 2 vào P(x) = ax 2 + bx + c ta được:
P(2) = a. 22 + b.2 + c
= 4a + 2b + c
Mà P(2) = 3 nên 4a + 2b + c = 3 (3)
• Từ (1), (2) ta có –b = 6 + b
Suy ra: –2b = 6
Do đó b = –3
• Thay b = –3 vào (1) ta được: a + c = 3
Suy ra c = 3 – a (4)
Thay b = –3 và c = 3 – a vào (3) ta được:
4a + 2.(–3) + 3 – a = 3
(4a – a) – 6 + 3 = 3
3a = 6
Do đó a = 2
Thay a = 2 vào (4) ta được c = 3 – 2 = 1
Do đó ta có: a = 2, b = –3 và c = 1.
Vậy P(x) = 2x2 – 3x + 1.
Câu 15. Người ta rót nước từ một can đựng 20 lít nước sang một bể rỗng có dạng hình lập phương với cạnh 40 cm. Khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là bao nhiêu? Biết rằng 1 lít = 1 dm3.
A. 20 – 0,4h (lít);
B. 20 + 0,4 (lít);
C. 20 + 0,4h (lít);
D. 20 – 0,4 (lít).
Đáp án: A
Giải thích:
Khi đổ nước vào trong bể sẽ có dạng hình hộp chữ nhật.
Khi đó thể tích của nước trong bể là:
20. 20. h
= 400. h (cm3)
= 0,4. h (dm3)
= 0,4h (lít).
Thể tích nước trong can còn lại là 20 – 0,4h lít.
Vậy ta chọn phương án A.
Các câu hỏi trắc nghiệm Toán 7 sách Cánh diều có đáp án, chọn lọc khác: