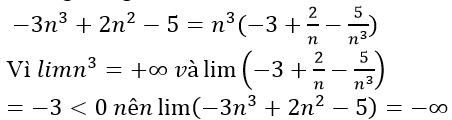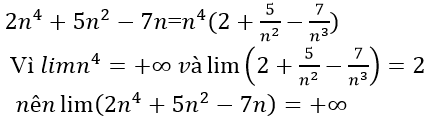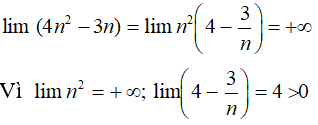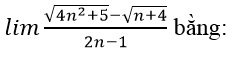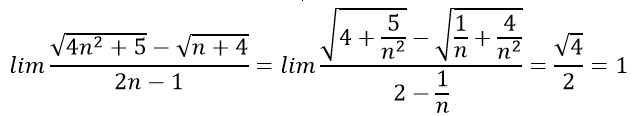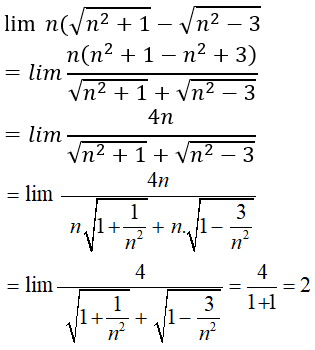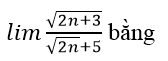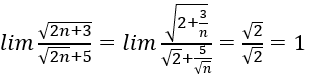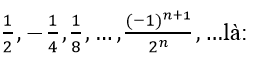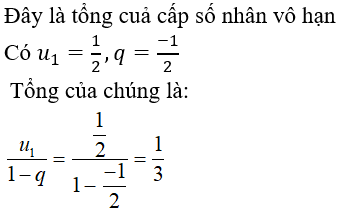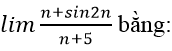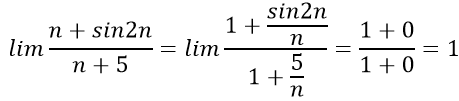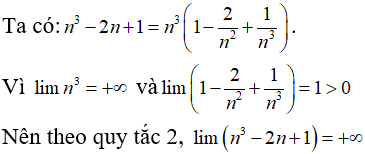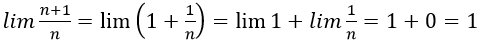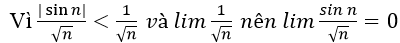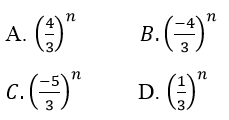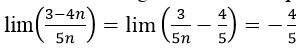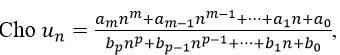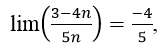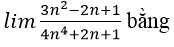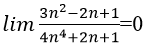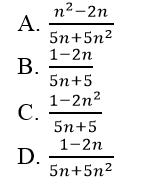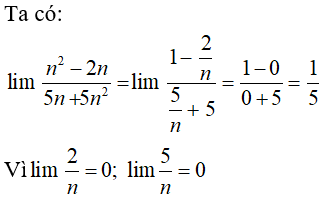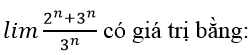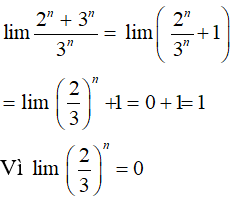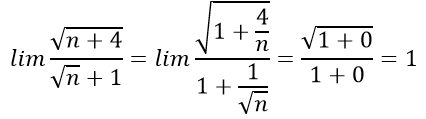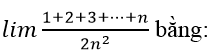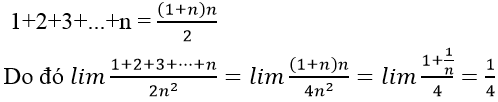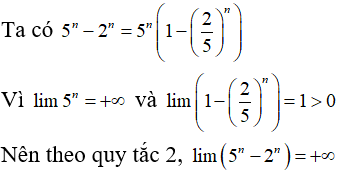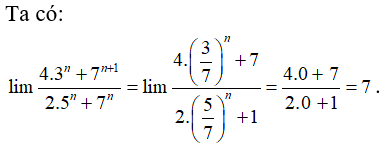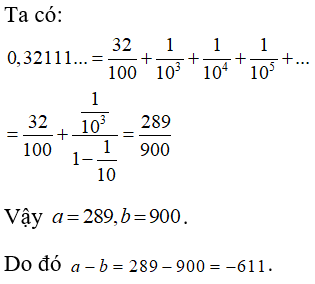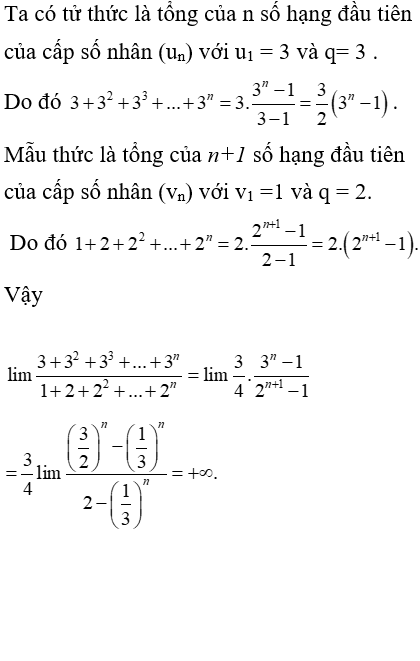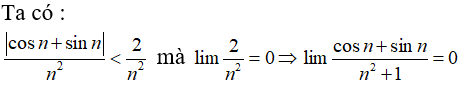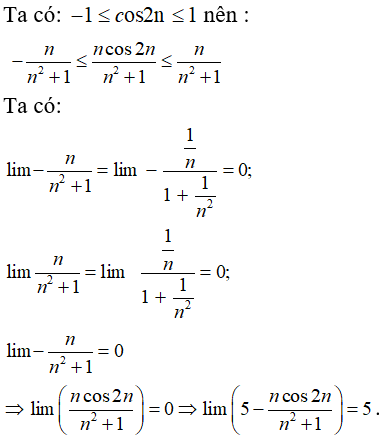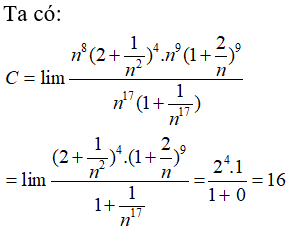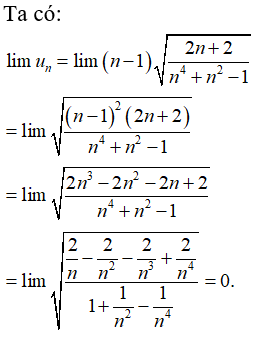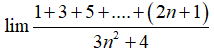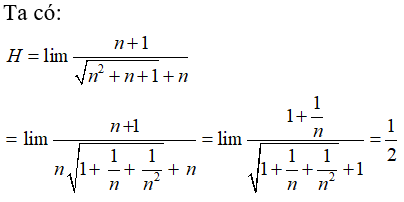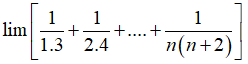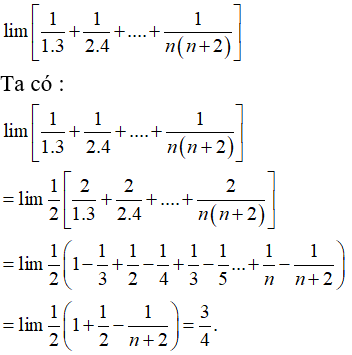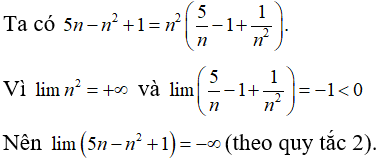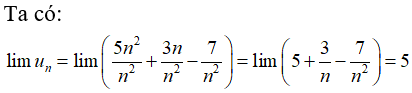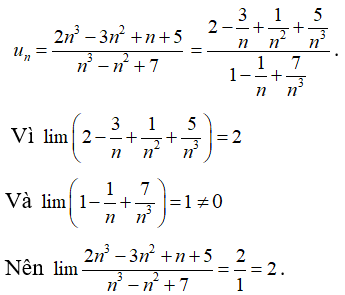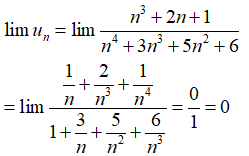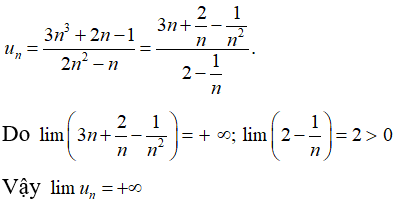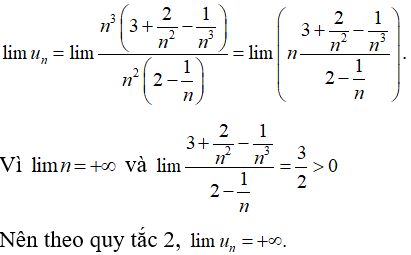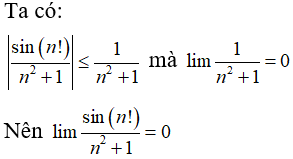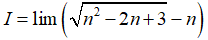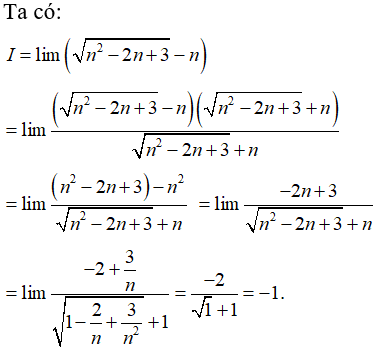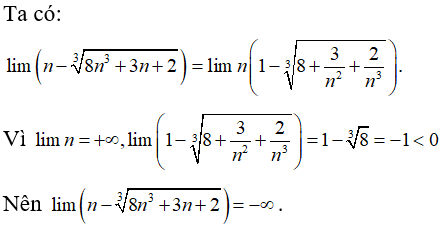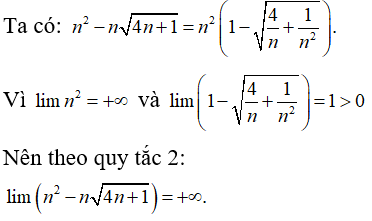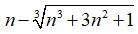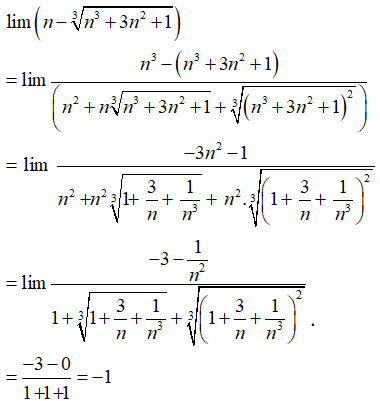Trắc nghiệm Toán học 11 Giới hạn của dãy số 

Bài 1: Cho số thập phân vô hạn tuần hoàn a = 2,151515... (chu kỳ 15), a được biểu diễn dưới dạng phân số tối giản, trong đó m, n là các số nguyên dương. Tìm tổng m + n.

A. 104

B. 312

C. 38 D . 114

Chọn đáp án A

Bài 2: lim⁡(-3n3+2n2-5) bằng:

A. -3    

B. 0    

C. -∞    

D. +∞

Ta có:

Chọn đáp án C

Bài 3: Lim(2n4+5n2-7n) bằng

A. -∞    

B. 0    

C. 2    

D. +∞

Ta có:

Chọn đáp án D

Bài 4: Dãy số nào sau đây có giưới hạn là +∞?

A. un=9n2-2n5    

B. un=n4-4n5

C. un=4n2-3n    

D. un=n3-5n4

Chỉ có dãy un=4n2-3n có giới hạn là +∞, các dãy còn lại đều có giới hạn là -∞. Đáp án C

Thật vậy, ta có:

Chọn đáp án C

Bài 5: Nếu limun=L,un+9>0 ∀n thì lim√(un+9) bằng số nào sau đây?

A. L+9    

B. L+3    

C. √(L+9)    

D. √L+3

Vì limun = L nên lim⁡(un + 9) = L + 9 do đó lim√(un + 9)=√(L + 9)

Chọn đáp án C

Bài 6:

A. 0  

B. 1   

C. 2   

D. +∞

- Cách 1: Chia tử thức và mẫu thức cho n:

Đáp án là B

- Cách 2: Thực chất có thể coi bậc cao nhất của tử thức và mẫu thức là 1, do đó chỉ cần để ý hệ số bậc 1 của tử thức là √4, của mẫu thức là 2, từ đó tính được kết quả bằng 1.

Chọn đáp án B

Bài 7: lim⁡n(√(n2+1)-√(n2-3)) bằng:

A. +∞     B. 4     C. 2     D. -1

Chọn đáp án C

Bài 8:

A. 5/7      

B. 5/2     

C. 1      

D.+∞

Chia cả tử và mẫu của phân thức cho √n, ta được:

Chọn đáp án C

Bài 9: Tổng của cấp số nhân vô hạn :

A. 1      

B. 1/3      

C. -1/3      

D. (-2)/3

Chọn đáp án B

Bài 10:

A. 2/5    

B. 1/5    

C. 0    

D. 1

Chia cả tử thức mẫu thức cho n , ta có:

Chọn đáp án D

Bài 11: Tính lim(n3 - 2n + 1)?

A. 0

B. 1

C. 2

D. $\infty$

Chọn đáp án D

Bài 12: Dãy số nào sau đây có giới hạn khác 0?

A. 1/n      

B. 1/√n     

 C. (n+1)/n      

D. (sin n)/√n

- Cách 1:

Đáp án C

- Cách 2 (phương pháp loại trừ): Từ các định lí ta thấy:

Các dãy ở phương án A,B đều bằng 0, do đó loại phương án A,B

Do đó loại phương án D.

Chọn đáp án C

Bài 13: Dãy số nào sau đây có giới hạn bằng 0?

- Cách 1: Dãy (1/3)n có giới hạn 0 vì |q| < 1 thì limqn = 0. Đáp án là D

- Cách 2: Các dãy ở các phương án A,B,C đều có dạng lim qn nhưng |q| > 1 nên không có giới hạn 0, do đó loại phương án A,B,C. Chọn đáp án D

Chọn đáp án D

Bài 14: lim((3-4n)/5n) có giá trị bằng:

A. 3/5      

B. -3/5      

C. 4/5     

D. -4/5

- Cách 1: Chia tử và mẫu của phân tử cho n (n là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức), ta được :

Chọn đáp án D

- Cách 2: Sử dụng nhận xét:

khi tính lim un ta thường chia tử và mẫu của phân thức cho nk (nk là luỹ thừa bậc cao nhất của n trong tử và mẫu của phân thức), từ đó được kết quả:

Nếu m < p thì lim un =0. Nếu m =p thì lim un=am/bp

Nếu m > p thì lim un= +∞ nếu am.bp > 0; lim un= -∞ nếu am.bp < 0

Vì tử và mẫu của phân thức đã cho đều có bậc 1 nên kết quả

Chọn đáp án D

Bài 15:

A. 0      

B. +∞      

C. 3/4      

D. 2/7

- Cách 1: Sử dụng nhận xét trên, vì bậc của tử thức nhỏ hơn bậc của mẫu thức nên kết quả :

Chọn đáp án A

Bài 16:

A. 0      

B. +∞      

C. 3/4     

D. 2/7

- Cách 1: Sử dụng nhận xét trên, vì bậc của tử thức lớn hơn bậc của mẫu thức, hệ số luỹ thừa bậc cao nhất của n cả tử và mẫu là số dương nên kết quả :

Chọn đáp án B

Bài 17: Dãy số nào sau đây có giới hạn bằng 1/5?

Chọn đáp án A

Bài 18:

A. 0      

B. 1      

C. 2/3      

D. 5/3

Chọn đáp án B

Bài 19:

A. 1      

B. 2      

C. 4      

D. +∞

Chia cả tử thức và mẫu thức cho √n

Chọn đáp án A

Bài 20:

A. 0    

B. 1/4    

C. 1/2    

D. +∞

Trước hết tính :

Chọn đáp án B

Bài 21: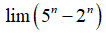 bằng :

A. -∞.

B. 3

C. +∞.

D. 5/2.

Chọn đáp án C

Bài 22: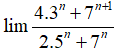 bằng :

A. 1

B. 7

C. 3/5

D. 7/5

Chọn đáp án B

Bài 23: Số thập phân vô hạn tuần hoàn 0,32111... được biểu diễn dưới dạng phân số tối giản a/b, trong đó a, b là các số nguyên dương. Tính a - b .

A. 611

B. 27901

C. - 611

D. -27901 .

Chọn đáp án C

Bài 24: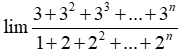 bằng:

A. +∞

B. 3

C. 3/2

D. 2/3

Chọn đáp án A

Bài 25 Giá trị của 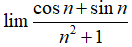 bằng:

:A. +∞

B. -∞

C. 0

D. 1

Chọn đáp án C

Bài 26: Kết quả đúng của 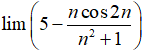 là:

A. 4

B. 5

C. –4

D. 1/4

Chọn đáp án B

Bài 27: Giá trị của 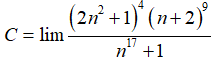 bằng:

A. +∞

B. -∞

C. 16

D. 1

Chọn đáp án C

Bài 28: Cho dãy số un với 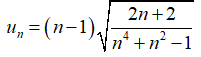. Chọn kết quả đúng của lim un là:

A. -∞

B. 0

C. 1

D. +∞

Chọn đáp án B

Bài 29: Tính giới hạn: 

A.0

B. 1/3

C. 2/3

D. 1

Chọn đáp án B

Bài 30: Giá trị của 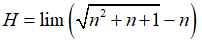 bằng:

A. +∞

B. -∞

C. 1/2

D. 1

Chọn đáp án C

Bài 31: Tính giới hạn: 

A. 3/4

B. 1

C. 0

D. 2/3

Chọn đáp án A

Bài 32: Tính lim(5n - n2 + 1)

A.

B.

C. 5.

D. -1

Chọn đáp án B

Bài 33: Tính lim un, với ?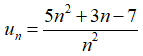

A. 5

B. 0

C. 3

D. - 7

Chọn đáp án A

Bài 34: Tính lim un với ?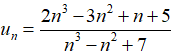

A. – 3

B. 1

C. 2

D. 0

Chia cả tử và mẫu của phân thức cho n3 (n3 là lũy thừa bậc cao nhất của n trong phân thức), ta được:

Chọn đáp án C

Bài 35: Giới hạn của dãy số (un) với 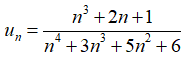 bằng

A. 1

B. 0

C.2

D.3

Chia cả tử và mẫu của phân thức cho n4 (n4 là bậc cao nhất của n trong phân thức), ta được

Chọn đáp án B

Bài 36: Giới hạn của dãy số (un) với 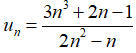, bằng

A. 3/2

B.0

C. +∞.

D. 1

Cách 1: Chia cả tử và mẫu cho n2 (n2 là lũy thừa bậc cao nhất của n trong mẫu thức), ta được :

Cách 2: Ta có:

Chọn đáp án C

Bài 37: bằng

A. 0

B.1

C. +∞

D. 2

Chọn đáp án A

Bài 38: Tính giới hạn 

A. I = -1

B. I = 1

C. I = 0

D. I = +∞

Chọn đáp án A

Bài 39: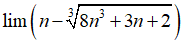 bằng:

A. +∞

B. -∞

C. -1

D. 0

Chọn đáp án B

Bài 40: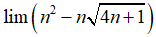 bằng:

A. – 1

B. 3

C. +∞

D. -∞

Chọn đáp án C

Bài 41: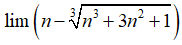 bằng :

A. – 1

B. 1

C. +∞

D. -∞

Ta tiến hành nhân chia với biểu thức liên hợp (bậc ba) của 

Chọn đáp án A