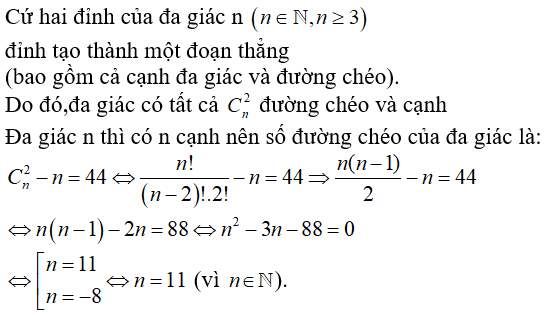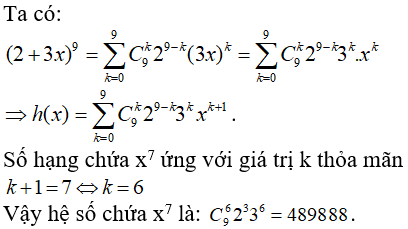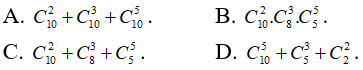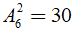Trắc nghiệm Toán học 11 Ôn tập chương 2: Tổ hợp, Xác suất

Bài 1: Một hộp đựng 4 bi xanh và 6 bi đỏ lần lượt rút 2 viên bi. Xác suất để rút được một bi xanh và 1 bi đỏ là:

Chọn đáp án D

Bài 2: Một nhóm học sinh gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một đội cờ đỏ sao cho phải có 1 đội trưởng nam, 1 đội phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập đội cờ đỏ.

A. 131444

B. 141666

C. 241561

D. 111300

Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:

Chọn đáp án D

Bài 3: Một lớp học có 20 nam và 26 nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự gồm 3 người. Hỏi có bao nhiêu cách chọn nếu trong ban cán sự có cả nam và nữ.

A. 11420

B. 11440

C. 14140

D. 53342

Chọn đáp án B

Bài 4: Từ 20 câu hỏi trắc nghiệm gồm 9 câu dễ, 7 câu trung bình và 4 câu khó người ta chọn ra 10 câu để làm đề kiểm tra sao cho phải có đủ cả 3 loại dễ, trung bình và khó. Hỏi có thể lập được bao nhiêu đề kiểm tra

A. 176860

B. 176435

C. 176451

D. 168637

Chọn đáp án C

Bài 5: Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác là:

A. 11.

B. 10.

C. 9.

D. 8.

Chọn đáp án A

Bài 6: Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt (n ≥ 2). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?

A. 16

B. 21

C. 30

D. 20

Chọn đáp án D

Bài 7: Trong khai triển 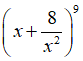, số hạng không chứa x là:

A. 4308.

B. 86016.

C. 84.

D. 43008.

Chọn đáp án D

Bài 8: Tìm hệ số của x7 trong khai triển biểu thức sau: h(x) = x(2 + 3x)9

A. 489889

B. 489887

C. -489888

D. 489888

Chọn đáp án D

Bài 9: Gieo hai con súc sắc. Xác suất để tổng hai mặt bằng 11 là.

Chọn đáp án A

Bài 10: Số cách chia 10 học sinh thành 3 nhóm lần lượt gồm 2, 3; 5 học sinh là:

Chọn đáp án B

Bài 11: Có hai hộp đựng bi. Hộp I có 9 viên bi được đánh số 1,2, ...; 9. Lấy ngẫu nhiên mỗi hộp một viên bi. Biết rằng xác suất để lấy được viên bi mang số chẵn ở hộp II là 3/10. Xác suất để lấy được cả hai viên bi mang số chẵn là:

Chọn đáp án A

Bài 12: Một hộp đựng 10 viên bi trong đó có 4 viên bi đỏ,3 viên bi xanh,2 viên bi vàng,1 viên bi trắng. Lấy ngẫu nhiên 2 bi tính xác suất biến cố : A: “2 viên bi cùng màu”

Chọn đáp án B

Bài 13: Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một cuốn tập thì số cách chọn khác nhau là:

A. 480

B. 24

C. 48

D. 60

Nếu chọn một cây bút chì thì sẽ có 8 cách. Nếu chọn một cây bút bi thì sẽ có 6 cách. Nếu chọn một cuốn tập thì sẽ có 10 cách. Theo qui tắc cộng, ta có 8 + 6+ 10 = 24 cách chọn.

Chọn đáp án B

Bài 14: Trong một cuộc thi tìm hiểu về đất nước Việt Nam, ban tổ chức công bố danh sách các đề tài bao gồm: 8 đề tài về lịch sử, 7 đề tài về thiên nhiên, 10 đề tài về con người và 6 đề tài về văn hóa. Mỗi thí sinh được quyền chọn một đề tài. Hỏi mỗi thí sinh có bao nhiêu khả năng lựa chọn đề tài?

A. 20

B. 3360

C. 31

D. 30

Nếu chọn đề tài về lịch sử có 8 cách. Nếu chọn đề tài về thiên nhiên có 7 cách. Nếu chọn đề tài về con người có 10 cách. Nếu chọn đề tài về văn hóa có 6 cách. Theo qui tắc cộng, ta có 8+ 7+ 10 + 6 = 31 cách chọn.

Chọn đáp án C

Bài 15: Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có mấy cách chọn lấy ba bông hoa có đủ cả ba màu.

A. 240

B. 210

C. 18

D. 120

Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có: Có 5 cách chọn hoa hồng trắng. Có 6 cách chọn hoa hồng đỏ. Có 7 cách chọn hoa hồng vàng. Vậy theo qui tắc nhân ta có 5.6.7= 210 cách.

Chọn đáp án B

Bài 16: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm một món ăn trong 5 món, một loại quả tráng miệng trong 5 loại quả tráng miệng và một nước uống trong 3 loại nước uống. Có bao nhiêu cách chọn thực đơn.

A. 25

B. 75

C. 100

D. 15

Để chọn thực đơn, ta có: Có 5 cách chọn món ăn. Có 5 cách chọn quả tráng miệng. Có 3 cách chọn nước uống. Vậy theo qui tắc nhân ta có 5.5.3 = 75cách.

Chọn đáp án B

Bài 17: Từ các chữ số 1; 5; 6; 7 có thể lập được bao nhiêu chữ số tự nhiên có 4 chữ số (không nhất thiết phải khác nhau) ?

A. 324

B. 256

C. 248

D. 124

Gọi số cần tìm có dạng 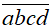 với (a, b, c, d) ∈ A = {1, 5, 6, 7} Vì số cần tìm có 4 chữ số không nhất thiết khác nhau nên: a được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn. b được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn. c được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn. d được chọn từ tập A (có 4 phần tử) nên có 4 cách chọn. Như vậy, ta có 4.4.4.4 = 256 số cần tìm.

Chọn đáp án B

Bài 18: Từ các chữ số 0; 1; 2; 3; 4; 5 có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau ?

A. 156

B. 144

C. 96

D. 134

Chọn đáp án A

Bài 19: Trong mặt phẳng cho một tập hợp gồm 6 điểm phân biệt. Có bao nhiêu vectơ khác vectơ 0Oxy→ có điểm đầu và điểm cuối thuộc tập hợp điểm này?

A. 15

B. 12

C. 1440

D. 30

Mỗi cặp sắp thứ tự gồm hai điểm (A; B) cho ta một vectơ có điểm đầu A và điểm cuối B và ngược lại. Như vậy, mỗi vectơ có thể xem là một chỉnh hợp chập 2 của tập hợp 6 điểm đã cho. Suy ra có

cách.

Chọn đáp án D

Bài 20: Trong một dạ hội cuối năm ở một cơ quan, ban tổ chức phát ra 100 vé xổ số đánh số từ 1 đến 100 cho 100 người. Xổ số có 4 giải: 1 giải nhất, 1 giải nhì, 1 giải ba, 1 giải tư. Kết quả là việc công bố ai trúng giải nhất, giải nhì, giải ba, giải tư. Hỏi có bao nhiêu kết quả có thể nếu biết rằng người giữ vé số 47 trúng một trong bốn giải?

A. 3766437

B. 3764637

C. 3764367

D. 3764376

Nếu người giữ vé số 47 trúng một trong bốn giải thì: Người giữ vé số 47 có 4 cách chọn giải. Ba giải còn lại ứng với một chỉnh hợp chấp 3 của 99 phần tử, do đó ta có cách .

Chọn đáp án D

Bài 21: Có bao nhiêu cách xếp 5 cuốn sách Toán, 6 cuốn sách Lý và 8 cuốn sách Hóa lên một kệ sách sao cho các cuốn sách cùng một môn học thì xếp cạnh nhau, biết các cuốn sách đôi một khác nhau.

A. 7.5!.6!.8!

B. 6.5!.6!.8!

C. 6.4!.6!.8!

D. 6.5!.6!.7!

Ta xếp các cuốn sách cùng một bộ môn thành một nhóm Trước hết ta xếp 3 nhóm lên kệ sách chúng ta có: 3! = 6 cách xếp Với mỗi cách xếp 3 nhóm đó lên kệ ta có 5! cách hoán vị các cuốn sách Toán, 6! cách hoán vị các cuốn sách Lý và 8! cách hoán vị các cuốn sách Hóa Vậy theo quy tắc nhân có tất cả: 6.5!.6!.8! cách xếp

Chọn đáp án B

Bài 22: Một hội đồng gồm 2 giáo viên và 3 học sinh được chọn từ một nhóm 5 giáo viên và 6 học sinh. Hỏi có bao nhiêu cách chọn?

A. 200

B. 150

C. 160

D. 180

Chọn đáp án A