Cho tam giác ABC cân ở A. Đường trung trực của cạnh AC cắt AB tại D
Lời giải Bài 86 trang 94 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Giải SBT Toán 7 Cánh diều Bài 12. Tính chất ba đường trung trực của tam giác
Bài 86 trang 94 SBT Toán 7 Tập 2: Cho tam giác ABC cân ở A. Đường trung trực của cạnh AC cắt AB tại D. Biết CD là tia phân giác của góc ACB. Tính số đo các góc của tam giác ABC.
Lời giải
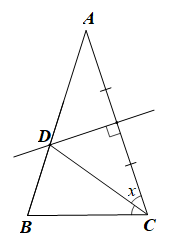
Đặt .
Vì CD là tia phân giác của góc ACB nên .
Vì tam giác ABC cân tại A nên AB = AC, .
Suy ra
Do điểm D nằm trên đường trung trực của AC nên DA = DC.
Do đó tam giác DAC cân ở D nên .
Xét ABC có (tổng ba góc của một tam giác)
Hay 2x + 2x + x = 180° nên 5x = 180°.
Suy ra x =180° : 5 = 36°.
Do đó .
Vậy số đo các góc A, B, C của tam giác ABC lần lượt là: 36°, 72°, 72°.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
