Giải sách bài tập Toán 7 Bài 12. Tính chất ba đường trung trực của tam giác

Bài 85 trang 94 SBT Toán 7 Tập 2: Cho hai tam giác đều chung đáy ABC và BCD. Gọi I là trung điểm của BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Đường thẳng BC là đường trung trực của AD.

b) Điểm I cách đều các điểm A, B, D.

c) Điểm B nằm trên đường trung trực của CD.

d) Điểm C không nằm trên đường trung trực của BD.

Lời giải

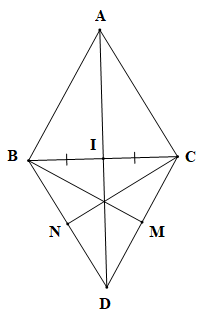
Vì tam giác ABC, DBC là tam giác đều nên AB = AC = BC = BD = DC.

• Ta có CA = CD nên C nằm trên đường trung trực của đoạn thẳng AD.

Do BA = BD nên B nằm trên đường trung trực của đoạn thẳng AD.

Suy ra BC là đường trung trực của đoạn thẳng AD.

Do đó phát biểu a là đúng.

• Vì BC = BD nên điểm B nằm trên đường trung trực của CD.

Do đó phát biểu c là đúng.

• Vì CB = CD nên điểm C nằm trên đường trung trực của BD.

Do đó phát biểu d là sai.

• Tam giác ABC là tam giác đều nên $\widehat{ABC}=60°$.

Trong tam giác ABI vuông tại I có $\widehat{IAB}+\widehat{IBA}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\widehat{IAB}=90°-\widehat{IBA}=90°-60°=30°$.

Xét tam giác ABI có $\widehat{ABI}>\widehat{IAB}$ (do 60° > 30°).

Suy ra AI > BI (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)

Do đó điểm I không cách đều hai điểm A và B nên phát biểu b là sai.

Vậy phát biểu a, c là đúng; phát biểu b, d là sai.

Bài 86 trang 94 SBT Toán 7 Tập 2: Cho tam giác ABC cân ở A. Đường trung trực của cạnh AC cắt AB tại D. Biết CD là tia phân giác của góc ACB. Tính số đo các góc của tam giác ABC.

Lời giải

Đặt $\widehat{DCA}=x$.

Vì CD là tia phân giác của góc ACB nên $\widehat{ACB}=2\widehat{ACD}=2\widehat{BCD}=2x$.

Vì tam giác ABC cân tại A nên AB = AC, $\widehat{ABC}=\widehat{ACB}$.

Suy ra $\widehat{ABC}=2x$

Do điểm D nằm trên đường trung trực của  AC nên DA = DC.

Do đó tam giác DAC cân ở D nên $\widehat{DAC}=\widehat{DCA}=x$.

Xét $∆$ABC có $\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180°$(tổng ba góc của một tam giác)

Hay 2x + 2x + x = 180° nên 5x = 180°.

Suy ra x =180° : 5 = 36°.

Do đó $\widehat{ACB}=\widehat{ABC}=2.36°=72°,\widehat{BAC}=36°$.

Vậy số đo các góc A, B, C của tam giác ABC lần lượt là: 36°, 72°, 72°.

Bài 87 trang 94 SBT Toán 7 Tập 2: Cho tam giác đều ABC có I là điểm cách đều ba cạnh AB, BC, CA. Chứng minh rằng I cách đều ba đỉnh A, B, C và cũng là trọng tâm của tam giác ABC.

Lời giải

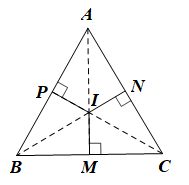
Gọi M, N, P lần lượt là hình chiếu của I trên BC, AC, AB.

Khi đó IM = IN = IP.

+) Chứng minh I cách đều ba đỉnh của tam giác ABC.

• Xét ∆AIP và ∆AIN có:

$\widehat{API}=\widehat{AQI}$  (cùng bằng 90°),

AI là cạnh chung,

IP = IN (chứng minh trên)

Do đó ∆AIP = ∆AIN (cạnh huyền – cạnh góc vuông)

Suy ra AP = AN (hai cạnh tương ứng) và $\widehat{PAI}=\widehat{NAI}$ (hai góc tương ứng).

Do đó AI là tia phân giác của góc BAC.

Mà $\widehat{BAC}=60°$ (do tam giác ABC đều).

Nên $\widehat{PAI}=\widehat{NAI}=30°$.

Xét tam giác API vuông tại P có: $\widehat{PAI}+\widehat{PIA}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\widehat{PIA}=90°-\widehat{PAI}=90°-30°=60°$

Chứng minh tương tự ta có: $\widehat{PIB}=60°$.

Xét ∆PIA và ∆PIB có:

$\widehat{API}=\widehat{BPI}=90°$ ,

PI là cạnh chung,

$\widehat{PIA}=\widehat{PIB}$  (cùng bằng 60°)

Do đó ∆PIA = ∆PIB (cạnh góc vuông – góc nhọn kề).

Suy ra IA = IB (hai cạnh tương ứng)

• Chứng minh tương tự ta cũng có IB = IC.

Do đó IA = IB = IC nên I cách đều ba đỉnh của tam giác ABC.

+) Chứng minh I là trọng tâm của tam giác ABC.

• Ta có ∆PIA = ∆PIB (chứng minh trên)

Suy ra PA = PB (hai cạnh tương ứng).

Do đó P là trung điểm của AB và điểm P cũng thuộc đường trung trực của AB.

Lại có IA = IB nên điểm I thuộc đường trung trực của AB.

CA = CB (do ∆ABC đều) nên điểm C thuộc đường trung trực của AB.

Do đó ba điểm P, I, C thẳng hàng.

Khi đó CP là đường trung truyến của tam giác ABC.

• Chứng minh tương tự ta cũng có AM, BN là các đường trung tuyến của tam giác ABC.

Mặt khác ba đường thẳng AM, BN, CP đều đi qua điểm I.

Do đó I là trọng tâm tam giác ABC.

Vậy I cách đều ba đỉnh A, B, C và cũng là trọng tâm của tam giác ABC.

Bài 88 trang 94 SBT Toán 7 Tập 2: Chứng minh rằng các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.

Lời giải

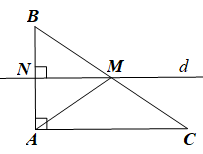
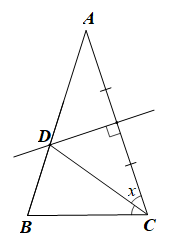
Gọi d là đường trung trực của cạnh AB và M là giao điểm của d và BC.

Do M ∈ d nên MA = MB hay tam giác MAB cân tại M.

Suy ra $\widehat{MBA}=\widehat{MAB}$ (1)

Trong tam giác vuông ABC có $\widehat{ABC}+\widehat{ACB}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Nên $\widehat{ACB}=90°-\widehat{ABC}$ (2)

Ta có $\widehat{BAM}+\widehat{MAC}=\widehat{BAC}=90°$

Nên $\widehat{MAC}=90°-\widehat{MBA}$ (3)

Từ (1), (2) và (3) suy ra $\widehat{MAC}=\widehat{MCA}$

Do đó tam giác MAC cân tại M nên MA = MC.

Như vậy, MB = MC (= MA) nên M là trung điểm của BC.

Vậy các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.

Bài 89 trang 94, 95 SBT Toán 7 Tập 2: Cho góc nhọn xOy và điểm M nằm trong góc xOy. Gọi E, F là hai điểm nằm ngoài góc xOy sao cho Ox là đường trung trực của đoạn thẳng ME, Oy là đường trung trực của đoạn thẳng MF (Hình 55).

Chứng minh:

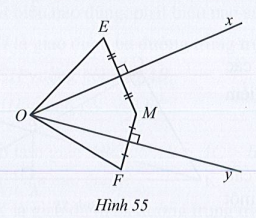
a) O là giao điểm ba đường trung trực của tam giác EMF.

b) Nếu $\widehat{xOy}=30°$ thì $\widehat{EOF}=60°$.

Lời giải

a) Trong tam giác EMF có O là giao điểm hai đường trung trực của ME và MF nên O là giao điểm ba đường trung trực của tam giác EMF.

Vậy O là giao điểm ba đường trung trực của tam giác FEM.

b)

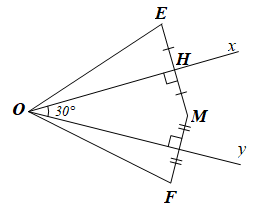
Gọi H là trung điểm của EM.

Xét ∆OEH và ∆OMH có:

$\widehat{OHE}=\widehat{OHM}\left(=90°\right)$,

OH là cạnh chung,

EH = MH (do H là trung điểm của EM).

Do đó ∆OEH = ∆OMH (hai cạnh góc vuông).

Suy ra $\widehat{\text{EOH}}=\widehat{MOH}$ (hai góc tương ứng).

Do đó Ox là tia phân giác của góc EOM nên $\widehat{\text{EOx}}=\widehat{xOM}=\frac{1}{2}\widehat{\text{EOM}}$

Hay $\widehat{EOM}=2\widehat{xOM}$.

Chứng minh tương tự ta cũng có: $\widehat{\text{FOy}}=\widehat{MOy}=\frac{1}{2}\widehat{\text{MOF}}$

Hay $\widehat{MOF}=2\widehat{MOy}$.

Ta có $\widehat{EOF}=\widehat{EOM}+\widehat{MOF}=2\widehat{xOM}+2\widehat{MOy}$

                  $=2\left(\widehat{xOM}+\widehat{MOy}\right)=2\widehat{xOy}=2.30°=60°$

Vậy nếu $\widehat{xOy}=30°$ thì $\widehat{EOF}=60°$.

Bài 90 trang 95 SBT Toán 7 Tập 2: Cho tam giác ABC cân ở A có $\widehat{BAC}=120°$. Đường trung trực của các cạnh AB và AC cắt nhau ở I và cắt cạnh BC lần lượt tại D, E (Hình 56).

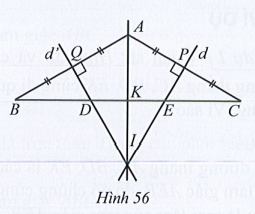
a) Chứng minh điểm I nằm trên đường trung trực của đoạn thẳng DE.

b) Đường tròn tâm I bán kính IA đi qua những điểm nào?

c) Tính số đo các góc của tam giác IBC.

Lời giải

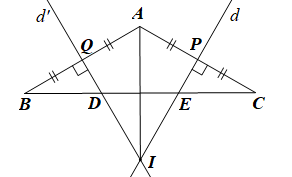
a) Gọi P và Q lần lượt là giao điểm của hai đường trung trực d, d’ với AC, AB.

• Vì tam giác ABC cân tại A nên AB = AC, $\widehat{B}=\widehat{C}$.

Vì Q là trung điểm của AB nên AQ = QB = $\frac{1}{2}$AB.

Vì P là trung điểm của AC nên AP = PC = $\frac{1}{2}$AC.

Mà AB = AC nên AQ = BQ = AP = CP.

• Xét ∆AQI và ∆API có:

$\widehat{AQI}=\widehat{API}\left(=90°\right)$,

AI là cạnh chung,

AQ = AP (chứng minh trên)

Do đó ∆AQI = ∆API (cạnh huyền – cạnh góc vuông).

Do đó QI = PI (hai cạnh tương ứng).

• Xét ∆BQD và ∆CPE có:

$\widehat{BQ\text{D}}=\widehat{CPE}\left(=90°\right)$,

$\widehat{B}=\widehat{C}$ (chứng minh trên),

BQ = CP (chứng minh trên)

Do đó ∆BQD = ∆CPE (cạnh góc vuông – góc nhọn kề).

Suy ra QD = PE (hai cạnh tương ứng).

• Ta có: QI = QD + DI và PI = PE + EI.

Mà QI = PI và QD = PE (chứng minh trên)

Do đó DI = EI nên điểm I nằm trên đường trung trực của đoạn thẳng DE.

Vậy điểm I nằm trên đường trung trực của đoạn thẳng DE.

b) Vì I nằm trên đường trung trực của AB nên IA = IB.

Vì I nằm trên đường trung trực của AC nên IA = IC.

Suy ra IA = IB = IC

Nên đường tròn tâm I bán kính IA đi qua các điểm A, B, C

Vậy đường tròn tâm I bán kính IA đi qua các điểm A, B, C.

c) Vì ∆AQI = ∆API (chứng minh câu a)

Nên $\widehat{QAI}=\widehat{PAI}$ (hai góc tương ứng)

Do đó AI là tia phân giác của góc BAC và $\widehat{BAI}=\widehat{CAI}=\frac{1}{2}\widehat{BAC}=\frac{1}{2}.120°=60°$

Xét tam giác ABI có IA = IB (chứng minh câu b) nên tam giác ABI cân tại I.

Lại có $\widehat{BAI}=60°$ nên tam giác ABI là tam giác đều.

Do đó IA = IB = AB.

Mà AB = AC, IA = IB = IC nên IA = IB = IC = AB = AC.

Xét $∆$BAC và $∆$BIC có:

AB = IB (chứng minh trên),

AC = IC (chứng minh trên),

BC là cạnh chung

Do đó ∆BAC = ∆BIC (c.c.c)

Suy ra $\widehat{ABC}=\widehat{IBC},\widehat{BAC}=\widehat{BIC}\widehat{,ACB}=\widehat{ICB}$ (các cặp góc tương ứng)

Xét ∆ABC có $\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°$ (tổng ba góc của một tam giác).

Mà $\widehat{BAC}=120°$ (giả thiết) và $\widehat{ABC}=\widehat{ACB}$ (do ∆ABC cân tại A).

Suy ra $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{BAC}}{2}=\frac{180°-120°}{2}=30°$.

Do đó $\widehat{IBC}=\widehat{ICB}=30°,\widehat{BIC}=120°$

Vậy $\widehat{IBC}=\widehat{ICB}=30°,\widehat{BIC}=120°$.

Bài 91* trang 95 SBT Toán 7 Tập 2: Cho tam giác ABC vuông cân ở A có đường phân giác AM. Gọi E là điểm nằm giữa B và C. Vẽ BH và CK vuông góc với AE (H, K thuộc AE).

a) Chứng minh ba đường trung trực tương ứng của các đoạn thẳng AB, AC, KH cùng đi qua điểm M.

b) Tính số đo các góc của tam giác MKH.

Lời giải

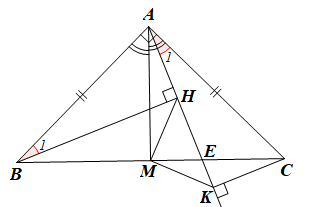
a) • Xét $∆$ABM và $∆$ACM có:

AB = AC (do $∆$ABC cân tại A),

$\widehat{BAM}=\widehat{CAM}$ (do AM là tia phân giác của góc BAC),

AM là cạnh chung

Do đó $∆$ABM = $∆$ACM (c.g.c)

Suy ra MB = MC (hai cạnh tương ứng).

• Ta có AM là tia phân giác của góc BAC nên:

$\widehat{BAM}=\widehat{CAM}=\frac{1}{2}\widehat{BAC}=\frac{1}{2}.90°=45°$

Lại có $\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°$ (tổng ba góc trong tam giác ABC)

Mà $\widehat{BAC}=90°$ và $\widehat{ABC}=\widehat{ACB}$ (do $∆$ABC cân tại A)

Nên $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{BAC}}{2}=\frac{180°-90°}{2}=45°$

Xét $∆$ABM có $\widehat{MBA}=\widehat{MAB}$ (cùng bằng 45°) nên tam giác ABM cân tại M.

Suy ra MA = MB

Mà MB = MC nên MA = MB = MC.

Do đó M nằm trên đường trung trực của AB và AC  (1)

• Trong tam giác ABH vuông tại H có ${\widehat{B}}_1+\widehat{BAH}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Nên ${\widehat{B}}_1=90°-\widehat{BAH}$

Mà ${\widehat{A}}_1=\widehat{BAC}-\widehat{BAH}=90°-\widehat{BAH}$

Suy ra ${\widehat{B}}_1={\widehat{A}}_1$

Xét $∆$BAH và $∆$ACK có:

$\widehat{BHA}=\widehat{AKC}\left(=90°\right)$,

${\widehat{B}}_1={\widehat{A}}_1$ (chứng minh trên),

AB = AC (chứng minh ở câu a),

Do đó ∆ABH = ∆CAK (cạnh n – góc nhọn).

Suy ra AH = CK (hai cạnh tương ứng) và $\widehat{BAH}=\widehat{ACK}$ (hai góc tương ứng).

Ta có $\widehat{BAH}=\widehat{BAM}+\widehat{MAH}=45°+\widehat{MAH}$

$\widehat{ACK}=\widehat{ACM}+\widehat{MCK}=45°+\widehat{MCK}$

Mà $\widehat{BAH}=\widehat{ACK}$ (chứng minh trên)

Suy ra $\widehat{MAH}=\widehat{MCK}$.

Xét ∆AMH và ∆CMK có:

AH = CK (chứng minh trên),

$\widehat{MAH}=\widehat{MCK}$ (chứng minh trên),

AM = AM (chứng minh ở câu a)

Do đó ∆AMH = ∆CMK (c.g.c)

Suy ra MH = MK (hai cạnh tương ứng)

Hay M nằm trên đường trung trực của HK (2)

Từ (1) và (2) ta có điểm M nằm trên đường trung trực của AB, AC, HK.

Vậy ba đường trung trực tương ứng của các đoạn thẳng AB, AC, KH cùng đi qua điểm M.

b) • Ta có $\widehat{AMH}=\widehat{CMK}$ (hai góc tương ứng của ∆AMH = ∆CMK).

Mà $\widehat{HMK}=\widehat{HMC}+\widehat{CMK}$

Do đó $\widehat{HMK}=\widehat{HMC}+\widehat{AMH}=\widehat{AMC}=90°$ nên tam giác MHK vuông tại H.

• Ta có MH = MK nên tam giác MHK cân tại M.

Suy ra $\widehat{MHK}=\widehat{MKH}$.

• Trong tam giác MHK vuông tại H có $\widehat{MHK}+\widehat{MKH}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Mà $\widehat{MHK}=\widehat{MKH}$ (chứng minh trên)

Suy ra $\widehat{MHK}=\widehat{MKH}=\frac{90°}{2}=45°$

Vậy $∆$MKH có $\widehat{MHK}=\widehat{MKH}=45°,\widehat{HMK}=90°$.