Giải sách bài tập Toán 7 Bài 5. Phép chia đa thức một biến

Bài 41 trang 53 SBT Toán 7 Tập 1: 

Tính:

a) $\left(\frac{3}{4}{x}^3\right):\left(-\frac{1}{2}{x}^2\right);$ 

b) (5xⁿ) : (4x²) (n ∈ ℕ, n ≥ 2);

c) $\left(x^3-3x^2+6x\right):\left(-\frac{1}{3}x\right);$ 

d) $\left(x+\frac{1}{3}{x}^2+\frac{7}{2}{x}^3\right):\left(5x\right).$ 

Lời giải

a) $\left(\frac{3}{4}{x}^3\right):\left(-\frac{1}{2}{x}^2\right)$$=\left[\frac{3}{4}:\left(-\frac{1}{2}\right)\right].\left(x^3:x^2\right)$ 

$=\frac{3}{4}.\frac{-2}{1}.x^{3-2}=-\frac{3}{2}x$;

b) (5xⁿ) : (4x²) = (5 : 4) . (xⁿ – x²) = $\frac{5}{4}$x^{n – 2} (n ∈ ℕ, n ≥ 2);

c) $\left(x^3-3x^2+6x\right):\left(-\frac{1}{3}x\right)$ 

$=\left[x^3:\left(-\frac{1}{3}x\right)\right]-\left[3x^2:\left(-\frac{1}{3}x\right)\right]+\left[6x:\left(-\frac{1}{3}x\right)\right]$

$=\left[1:\left(-\frac{1}{3}\right)\right].\left(x^3:x\right)-\left[3:\left(-\frac{1}{3}\right)\right].\left(x^2:x\right)+\left[6:\left(-\frac{1}{3}\right)\right].\left(x:x\right)$

= 1 . (–3) . x^{3 – 1}  – 3 . (–3) . x^{2 – 1} + 6 . (–3) . x^{1 – 1}

= –3x² + 9x – 18;

d) $\left(x+\frac{1}{3}{x}^2+\frac{7}{2}{x}^3\right):\left(5x\right)$ 

$=\left(x:5x\right)+\left(\frac{1}{3}{x}^2:5x\right)+\left(\frac{7}{2}{x}^3:5x\right)$

$=\left(1:5\right).\left(x:x\right)+\left(\frac{1}{3}:5\right).\left(x^2:x\right)+\left(\frac{7}{2}:5\right).\left(x^3:x\right)$

$=\frac{1}{5}.x^{1-1}+\frac{1}{3}.\frac{1}{5}.x^{2-1}+\frac{7}{2}.\frac{1}{5}.x^{3-1}$

$=\frac{1}{5}{x}^0+\frac{1}{15}{x}^1+\frac{7}{10}{x}^2$

$=\frac{1}{5}+\frac{1}{15}x+\frac{7}{10}{x}^2.$

Bài 42 trang 53, 54 SBT Toán 7 Tập 1: 

a) Cho đa thức $P\left(x\right)=\left(6x^5-\frac{1}{2}{x}^4+\frac{1}{3}{x}^3\right):\left(2x^3\right).$ Rút gọn rồi tính giá trị của P(x) tại x = –2.

b) Cho đa thức $Q\left(x\right)=3\left(\frac{2x}{3}-1\right)+\left(15x^2-10x\right):\left(-5x\right)-\left(3x-1\right)$. Rút gọn rồi tính giá trị của Q(x) tại $x=\frac{1}{3}$.

Lời giải

a) $P\left(x\right)=\left(6x^5-\frac{1}{2}{x}^4+\frac{1}{3}{x}^3\right):\left(2x^3\right)$

$=\left(6x^5:2x^3\right)-\left(\frac{1}{2}{x}^4:2x^3\right)+\left(\frac{1}{3}{x}^3:2x^3\right)$

$=\left(6:2\right).\left(x^5:x^3\right)-\left(\frac{1}{2}:2\right).\left(x^4:x^3\right)+\left(\frac{1}{3}:2\right).\left(x^3:x^3\right)$

$=3.x^{5-3}-\frac{1}{4}.x^{4-3}+\frac{1}{6}.x^{3-3}$

$=3.x^2-\frac{1}{4}.x^1+\frac{1}{6}.x^0$

$=3x^2-\frac{1}{4}x+\frac{1}{6}.$

Thay x = –2 vào $P\left(x\right)=3x^2-\frac{1}{4}x+\frac{1}{6}$ ta được:

$P\left(-2\right)=3.{\left(-2\right)}^2-\frac{1}{4}.\left(-2\right)+\frac{1}{6}=3.4+\frac{1}{2}+\frac{1}{6}$

           $=\frac{72+3+1}{6}=\frac{76}{6}=\frac{38}{3}.$

Vậy tại x =  –2 thì P(x) có giá trị bằng $\frac{38}{3}.$ 

b) $Q\left(x\right)=3\left(\frac{2x}{3}-1\right)+\left(15x^2-10x\right):\left(-5x\right)-\left(3x-1\right)$

$=3.\frac{2x}{3}-3.1+\left[15x^2:\left(-5x\right)\right]-\left[10x:\left(-5x\right)\right]-3x+1$

= 2x – 3 + (–3x) – (– 2) – 3x + 1

= [2x + (– 3x) – 3x] + [– 3 – (–2) + 1]

= – 4x.

Thay $x=\frac{1}{3}$ vào Q(x) = – 4x ta được:

$Q\left(\frac{1}{3}\right)=-4.\frac{1}{3}=-\frac{4}{3}.$

Vậy tại $x=\frac{1}{3}$ thì Q(x) có giá trị bằng $-\frac{4}{3}.$ 

Bài 43 trang 54 SBT Toán 7 Tập 1: 

Khi giải bài tập “Xét xem đa thức A(x) = – 12x⁴ + 5x³ + 15x² có chia hết cho đơn thức B(x) = 3x² hay không”, bạn Hồng nói “Đa thức A(x) không chia hết cho đơn thức B(x) vì 5 không chia hết cho 3”, còn bạn Hà nói “Đa thức A(x) chia hết cho đơn thức B(x) vì số mũ của biến ở mỗi đơn thức của A(x) đều lớn hơn hoặc bằng số mũ của biến đó trong B(x)”. Theo em, bạn nào nói đúng?

Lời giải

Theo em, bạn Hà nói đúng. Vì:

A(x) : B(x) = (– 12x⁴ + 5x³ + 15x²) : (3x²)

= (– 12x⁴ : 3x²) + (5x³ : 3x²) + (15x² : 3x²)

= –4x² + $\frac{5}{3}$x + 5.

Do đó A(x) ⋮ B(x).

Vậy bạn Hà nói đúng.

Bài 44 trang 54 SBT Toán 7 Tập 1: Tính:

a) (3x³ – 7x² + 4x – 4) : (x – 2);

b) (x⁵ + x + 1) : (x³ – x).

Lời giải

a) (3x³ – 7x² + 4x – 4) : (x – 2)

Ta thực hiện đặt tính chia đa thức như sau:

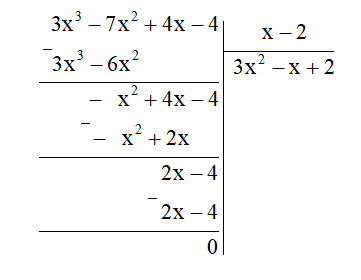
Vậy (3x³ – 7x² + 4x – 4) : (x – 2) = 3x² – x + 2.

b) (x⁵ + x + 1) : (x³ – x).

Ta thực hiện đặt tính chia đa thức như sau:

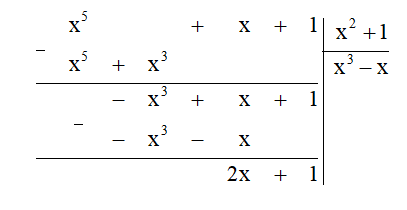
Vậy (x⁵ + x + 1) : (x³ – x) = x³ – x (dư 2x + 1).

Bài 45 trang 54 SBT Toán 7 Tập 1: 

Cho đa thức P(x) = 3x³ – 2x² + 5. Chia đa thức P(x) cho đa thức Q(x) (Q(x) ≠ 0) được thương là đa thức S(x) = 3x – 2 và dư là đa thức R(x) = 3x + 3. Tìm đa thức Q(x).

Lời giải

Dựa vào quy tắc phép chia ta có:

P(x) = Q(x) . S(x) + R(x)

Hay P(x) – R(x) = Q(x) . S(x)

Suy ra Q(x) = [P(x) – R(x)] : S(x)

Do đó Q(x) = [(3x³ – 2x² + 5) – (3x + 3)] : (3x – 2)

                   = (3x³ – 2x² + 5 – 3x – 3) : (3x – 2)

                   = (3x³ – 2x² – 3x + 2) : (3x – 2)

Ta thực hiện đặt tính chia đa thức như sau:

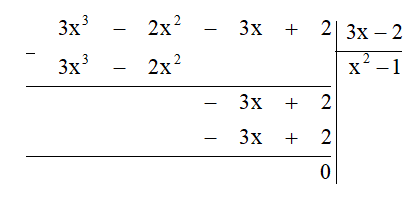
Khi đó Q(x) = (3x³ – 2x² – 3x + 2) : (3x – 2) = x² – 1.

Vậy Q(x) = x² – 1.

Bài 46 trang 54 SBT Toán 7 Tập 1: 

a) Tìm số dư của phép chia đa thức 4x⁴ – 2x² + 7 cho x + 3.

b) Tìm đa thức bị chia, biết đa thức chia là x² – 2x + 3, thương là x² – 2, dư là 9x – 5.

Lời giải

a) Ta thực hiện đặt tính chia đa thức như sau:

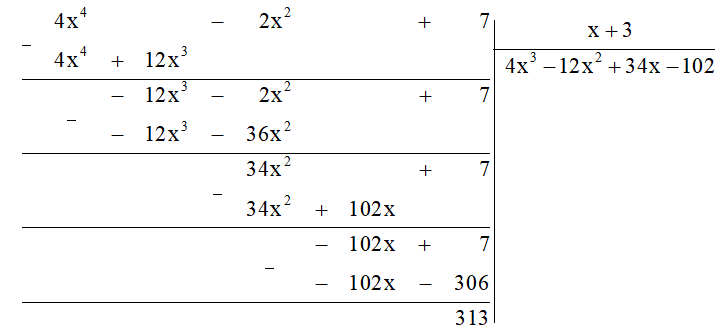
Vậy thực hiện phép chia đa thức 4x⁴ – 2x² + 7 cho x + 3, ta được thương là 4x³ – 12x² + 34x – 102 và số dư là 313.

b) Dựa vào quy tắc phép chia ta có đa thức bị chia là:

(x² – 2x + 3) . (x² – 2) + (9x – 5)

= x² . (x² – 2) – 2x . (x² – 2) + 3 . (x² – 2) + 9x – 5

= x⁴ – 2x² – 2x³ + 4x + 3x² – 6 + 9x – 5

= x⁴ – 2x³ + (– 2x² + 3x²) + (4x + 9x) + (– 6 – 5)

= x⁴ – 2x³ + x² + 13x – 11

Vậy đa thức bị chia cần tìm là x⁴ – 2x³ + x² + 13x – 11.

Bài 47 trang 54 SBT Toán 7 Tập 1: 

a) Tìm số a sao cho 10x² – 7x + a chia hết cho 2x – 3.

b) Tìm số a sao cho x³ – 10x + a chia hết cho x – 2.

Lời giải

a) Ta thực hiện đặt tính chia đa thức như sau:

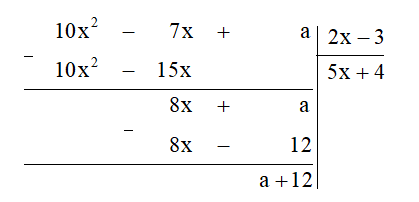
Do đó số dư của phép chia là a + 12.

Để 10x² – 7x + a chia hết cho 2x – 3 thì số dư bằng 0, tức là a + 12 = 0.

Suy ra a = –12.

Vậy a = –12 thì 10x² – 7x + a chia hết cho 2x – 3.

b) Ta thực hiện đặt tính chia đa thức như sau:

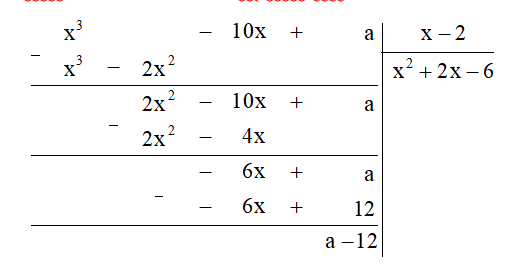
Do đó số dư của phép chia trên là a – 12.

Để   x³ – 10x + a chia hết cho x – 2 thì số dư bằng 0, tức là a – 12 = 0.

Suy ra a = 12.

Vậy a = 12 thì x³ – 10x + a chia hết cho x – 2.

Bài 48* trang 54 SBT Toán 7 Tập 1: 

Tìm n ∈ ℤ để 2n² – n chia hết cho n + 1.

Lời giải

Ta thực hiện đặt tính chia đa thức như sau:

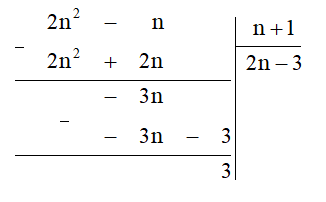
Do đó $\frac{2n^2-n}{n+1}=2n-3+\frac{3}{n+1}$ (với n + 1 ≠ 0).

Với n ∈ ℤ để 2n² – n chia hết cho n + 1 thì 3 ⋮ (n + 1).

Điều này xảy ra khi và chỉ khi (n + 1) ∈ Ư(3) = {–1; 1; –3; 3}.

Ta có bảng sau:

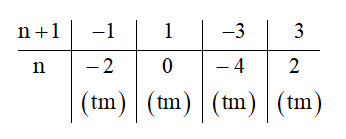
Vậy n ∈ {–4; –2; 0; 3}.

Bài 49 trang 54 SBT Toán 7 Tập 1: 

Một mảnh đất có dạng hình thang vuông với đáy bé là 10 m, chiều cao là 2x + 5 (m). Người ta mở rộng mảnh đất đó để được mảnh đất có dạng hình chữ nhật như Hình 6. Biết diện tích của phần đất mở rộng (phần tô đậm) là 6x² + 13x – 5 (m²), tính diện tích của mảnh đất lúc ban đầu.

Lời giải

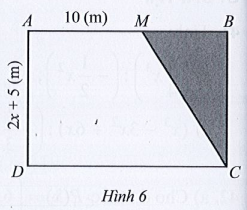
Quan sát Hình 6 ta thấy chiều cao kẻ từ C của tam giác BMC cũng là chiều cao của hình thang vuông AMCD.

Ta có diện tích của tam giác BMC được tính là:

$\frac{1}{2}$ . BM . BC = $\frac{1}{2}$ . BM . (2x + 5) (m²).

Mà theo bài diện tích phần đất dạng tam giác BMC là 6x² + 13x – 5 (m²).

Do đó $\frac{1}{2}$ . BM . (2x + 5) = 6x² + 13x – 5

Hay BM . (2x + 5) = 2 . (6x² + 13x – 5)

Suy ra BM = [2 . (6x² + 13x – 5)] : (2x + 5)

Hay BM = (12x² + 26x – 10) : (2x + 5).

Ta thực hiện đặt tính chia đa thức như sau:

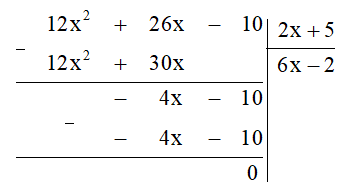
Khi đó BM = 6x – 2 (m).

Suy ra AB = AM + MB = 10 + 6x – 2 = 6x + 8 (m).

Diện tích của mảnh đất hình thang vuông ban đầu là:

$\frac{1}{2}$ . [10 + (6x + 8)] . (2x + 5) = $\frac{1}{2}$ . (6x + 18) . (2x + 5)

= (3x + 9) . (2x + 5) = 3x . (2x + 5) + 9 . (2x + 5)

= 6x² + 15x + 18x + 45 = 6x² + 33x + 45 (m²).

Vậy diện tích của mảnh đất hình thang vuông ban đầu là 6x² + 33x + 45 (m²).