Giải sách bài tập Toán 7 Bài tập cuối chương 7

Bài 99 trang 98 SBT Toán 7 Tập 2:

Cho hai tam giác ABC và MNP có $\widehat{ABC}=\widehat{MNP},$ $\widehat{ACB}=\widehat{MPN}.$ Cần thêm một điều kiện để tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc – cạnh – góc là:

A. AC = MP;

B. AB = MN;

C. BC = NP;

D. AC = MN.

Lời giải

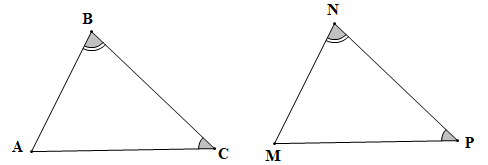
Để ΔABC = ∆MNP theo trường hợp góc – cạnh – góc thì hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh bằng nhau của hai tam giác.

Mà $\widehat{ABC}=\widehat{MNP},\widehat{ACB}=\widehat{MPN}$ 

Lại có $\widehat{ABC}$ và $\widehat{ACB}$ là hai góc kề cạnh BC;

$\widehat{MNP}$ và $\widehat{MPN}$ là hai góc kề cạnh NP.

Do đó điều kiện còn thiếu là điều kiện về cạnh, đó là BC = NP.

Vậy ta chọn đáp án C.

Bài 100 trang 98 SBT Toán 7 Tập 2: Cho tam giác ABC có $\widehat{BAC}=110°$. Các đường trung trực của AB và AC cắt cạnh BC lần lượt tại E và F. Khi đó, số đo góc EAF bằng:

A. 20°;

B. 30°;

C. 40°;

D. 50°.

Lời giải

Xét tam giác ABC có:

$\widehat{B}+\widehat{C}+\widehat{BAC}=180°$ (tổng ba góc trong một tam giác)

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{BAC}=180°-110°=70°$.

Vì E thuộc đường trung trực của AB nên EB = EA.

Do đó tam giác ABE cân tại E nên $\widehat{EAB}=\widehat{B}$.

Vì F thuộc đường trung trực của AC nên FC = FA.

Do đó tam giác ACF cân tại F nên $\widehat{F\text{A}C}=\widehat{C}$.

Ta có $\widehat{BA\text{E}}+\widehat{E\text{A}F}+\widehat{FAC}=\widehat{BAC}$

Hay $\widehat{B}+\widehat{E\text{A}F}+\widehat{C}=\widehat{BAC}$

Do đó $\widehat{E\text{A}F}=\widehat{BAC}-\left(\widehat{B}+\widehat{C}\right)$

Suy ra $\widehat{E\text{A}F}=110°-70°=40°$.

Vậy ta chọn đáp án C.

Bài 101 trang 98 SBT Toán 7 Tập 2:  Trong các hình 62a, 62b, 62c, 62d, hình nào có điểm cách đều các đỉnh của tam giác đó? Vì sao?

Lời giải

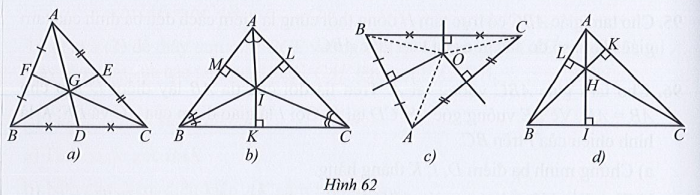
• Hình 62a:

Xét tam giác ABC có G là giao điểm của ba đường trung tuyến AD, BE, CF nên G là trọng tâm của tam giác ABC.

Do đó G không cách đều ba đỉnh của tam giác ABC

• Hình 62b:

Xét tam giác ABC có I là giao điểm của ba đường phân giác AI, BI, CI nên I cách đều ba cạnh của tam giác ABC.

Do đó I không cách đều ba đỉnh của tam giác ABC

• Hình 62c:

Xét tam giác ABC có O là giao điểm của ba đường trung trực nên OA = OB = OC.

Do đó O cách đều ba đỉnh của tam giác ABC.

• Hình 62d:

Xét tam giác ABC có H là giao điểm của ba đường cao AI, BK, CL nên H là trực tâm của tam giác ABC.

Do đó H không cách đều ba đỉnh của tam giác ABC.

Vậy hình 62c có điểm O cách đều các đỉnh của tam giác ABC.

Bài 102* trang 98 SBT Toán 7 Tập 2: Cho tam giác ABC và điểm G nằm trong tam giác. Chứng minh: Nếu diện tích các tam giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.

Lời giải

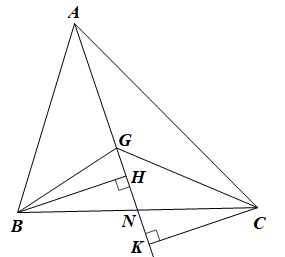
Gọi N là giao điểm của AG và BC.

Kẻ BH ⊥ AN (H ∈ AN) và CK ⊥ AN (K ∈ AN).

• Ta có:

$S_{\Delta GAB}=\frac{AG.BH}{2},S_{\Delta GCA}=\frac{AG.CK}{2}$

Mà $S_{\Delta AGB}=S_{\Delta AGC}$ nên $\frac{AG.BH}{2}=\frac{AG.CK}{2}$ 

Suy ra BH = CK.

• Xét $∆$BHN và $∆$CKN có

$\widehat{BHN}=\widehat{CKN}(=90°)$,

BH = CK (chứng minh trên),

$\widehat{HNB}=\widehat{KNC}$ (hai góc đối đỉnh)

Do đó ∆BHN = ∆CKN (g.c.g)

Suy ra BN = CN (hai cạnh tương ứng)

Hay AN là đường trung tuyến của tam giác ABC.

• Chứng minh tương tự, ta có CG cũng là đường trung tuyến của tam giác ABC.

Tam giác ABC có AN, CG là hai đường trung tuyến cuả tam giác

Mà AN và CG cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Vậy nếu diện tích các tam giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.

Bài 103 trang 98 SBT Toán 7 Tập 2: Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC; H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Chứng minh:

a) OC vuông góc với FH;

b) Tam giác OAI là tam giác cân;

c) Tam giác BAI là tam giác cân.

Lời giải

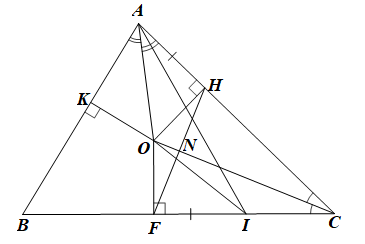
a) Xét $∆$OHC và $∆$OFC có:

$\widehat{OHC}=\widehat{OFC}(=90°)$,

OC là cạnh chung,

$\widehat{OCH}=\widehat{OCF}$ (do CO là tia phân giác của góc ACB)

Do đó ∆OHC = ∆OFC (cạnh huyền – góc nhọn)

suy ra CH = CF, OH = OF (các cặp cạnh tương ứng).

Do đó C và O cùng nằm trên đường trung trực của đoạn thẳng FH.

Hay CO là đường trung trực của đoạn thẳng FH.

Do đó OC ⊥ FH.

Vậy OC ⊥ FH.

b) Xét ∆OHA và ∆OFI có:

$\widehat{OHA}=\widehat{OFI}\left(=90°\right)$,

OH = OF (chứng minh câu a),

AH = IF (giả thiết),

Do đó ∆OHA = ∆OFI (hai cạnh góc vuông)

Suy ra OA = OI (hai cạnh tương ứng)

Tam giác OAI có OA = OI nên ∆OAI cân tại O.

Vậy tam giác OAI là tam giác cân tại O.

c) • Kẻ OK ⊥ AB (K ∈ AB).

Xét $∆$AOH và $∆$AOK có

$\widehat{OHA}=\widehat{OK\text{A}}(=90°)$,

OA là cạnh chung,

$\widehat{HAO}=\widehat{KAO}$ (do AO là tia phân giác của góc BAC)

Do đó ∆AOH = ∆AOK (cạnh huyền – góc nhọn)

Suy ra AH = AK (hai cạnh tương ứng).

• Xét tam giác ABC có O là giao điểm của hai tia phân giác của góc ACB và BAC.

Suy ra BO là tia phân giác của góc ABC.

Xét $∆$BOK và $∆$BOF có

$\widehat{OKB}=\widehat{OFB}(=90°)$,

OB là cạnh chung,

$\widehat{KBO}=\widehat{FBO}$ (do BO là tia phân giác của góc ABC)

Do đó ∆BOK = ∆BOF (cạnh huyền – góc nhọn).

Suy ra BK = BF (hai cạnh tương ứng)

• Ta có AB = AK + KB, BI = BF + FI

Mà BK = BF, AK = IF (= AH)

Từ đó suy ra AB = BI nên tam giác BAI cân tại B.

Vậy tam giác BAI cân tại B.

Bài 104 trang 99 SBT Toán 7 Tập 2: Cho tam giác ABC có AB < AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.

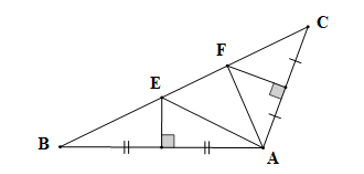
a) Chứng minh AC = EB và AC song song với EB.

b) Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. CHứng minh ba điểm I, M, K thẳng hàng.

c) Từ E kẻ EH vuông góc với BC tại H. Cho biết $\widehat{HBE}=50°;\widehat{MEB}=25°$. Tính số đo các góc HEB và HEM.

Lời giải

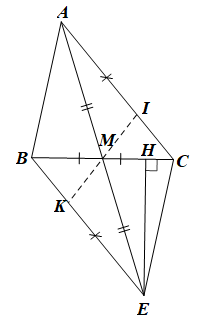
a) Xét $∆$AMC và $∆$EMB có:

AM = ME (giả thiết),

$\widehat{AMC}=\widehat{EMB}$ (hai góc đối đỉnh),

BM = CM (vì M là trung điểm của BC)

Do đó ∆AMC = ∆EMB (c.g.c)

Suy ra AC = EB (hai cạnh tương ứng) và $\widehat{MAC}=\widehat{MEB}$ (hai góc tương ứng)

Mà $\widehat{MAC}$ và $\widehat{MEB}$ ở vị trí so le trong nên AC // BE.

Vậy AC = EB và AC song song với EB.

b) Xét $∆$AMI và $∆$EMK có:

AM = ME (giả thiết),

$\widehat{MAI}=\widehat{MEK}$ (do $\widehat{MAC}=\widehat{MEB}$),

AI = EK (giả thiết)

Do đó ∆AMI = ∆EMK (c.g.c)

Suy ra $\widehat{AMI}=\widehat{EMK}$ (hai góc tương ứng)

Mà $\widehat{AMI}+\widehat{IME}=180°$ (hai góc kề bù)

Suy ra $\widehat{EMK}+\widehat{IME}=180°$

Hay $\widehat{IMK}=180°$

Do đó ba điểm I, M, K thẳng hàng.

Vậy ba điểm I, M, K thẳng hàng.

c) Trong tam giác HBE vuông tại H có:

$\widehat{HBE}+\widehat{HEB}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\widehat{HEB}=90°-\widehat{HBE}=90°-50°=40°$.

Ta có $\widehat{HEB}=\widehat{HEM}+\widehat{MEB}$ (hai góc kề nhau)

Hay $40°=\widehat{HEM}+25°$

Suy ra $\widehat{HEM}=40°-25°=15°$.

Vậy $\widehat{HEB}=40°;\widehat{HEM}=15°$.

Bài 105 trang 99 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có các đường cao BD và CE cắt nhau tại H.

a) Chứng minh ∆ADB = ∆AEC.

b) Chứng minh tam giác HDE là tam giác cân.

c) So sánh HB và HD.

d) Gọi M là trung điểm của HC, N là trung điểm của HB, I là giao điểm của BM và CN. Chứng minh ba điểm A, H, I thẳng hàng.

Lời giải

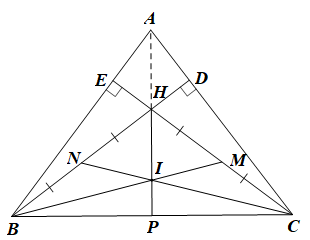
a) Xét $∆$ABD và $∆$ACE có:

$\widehat{ADB}=\widehat{AEC}\left(=90°\right)$,

AB = AC (do tam giác ABC cân tại A),

$\widehat{A}$ là góc chung,

Suy ra ∆ADB = ∆AEC (cạnh huyền – góc nhọn).

Vậy ∆ADB = ∆AEC.

b) Vì ∆ADB = ∆AEC (chứng minh câu a)

Suy ra AD = AE (hai cạnh tương ứng) và $\widehat{ABD}=\widehat{ACE}$ (hai góc tương ứng).

Ta có AB = AE + EB, AC = AD + DC.

Mà AB = AC, AE = AD.

Suy ra BE = CD.

Xét $∆$EHB và $∆$DHC có:

$\widehat{HEB}=\widehat{H\text{D}C}\left(=90°\right)$,

BE = CD (chứng minh trên),

$\widehat{EBH}=\widehat{DCH}$ (do $\widehat{ABD}=\widehat{ACE}$)

Suy ra ∆EHB = ∆DHC (cạnh góc vuông – góc nhọn kề).

Do đó HE = HD, BH = CH (các cặp cạnh tương ứng).

Tam giác HDE có HE = HD nên tam giác HDE cân tại H.

Vậy tam giác HDE là tam giác cân tại H.

c) Trong tam giác vuông HDC có HC > HD (trong tam giác vuông, cạnh huyền là cạnh lớn nhất)

Mà HC = HB (chứng minh câu b)

Do đó HB > HD.

Vậy HB > HD.

d) • Gọi P là giao điểm của HI và BC.

Tam giác HBC có BM và CN là hai đường trung tuyến cắt nhau tại I.

Do đó I là trọng tâm của tam giác HBC nên HP là đường trung tuyến xuất phát từ đỉnh H của tam giác.

Từ đó ta có PB = PC.

Xét $∆$HBP và $∆$HCP có:

HB = HC (chứng minh ở câu b),

HP là cạnh chung,

PB = PC (chứng minh trên)

Do đó $∆$HBP = $∆$HCP (c.c.c)

Suy ra $\widehat{HPB}=\widehat{HPC}$ (hai góc tương ứng)

Mà $\widehat{HPB}+\widehat{HPC}=180°$ (hai góc kề bù)

Do đó $\widehat{HPB}=\widehat{HPC}=\frac{180°}{2}=90°$

Từ đó ta có HP ⊥ BC hay HI ⊥ BC (1)

• Tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm của tam giác ABC.

Do đó AH ⊥ BC (2)

Từ (1) và (2) suy ra ba điểm A, H, I cùng nằm trên một đường thẳng vuông góc với BC tại P

Hay ba điểm A, H, I thẳng hàng.

Vậy ba điểm A, H, I thẳng hàng.

Bài 106 trang 99 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.

a) Chứng minh $\widehat{ABD}=\widehat{AED}$.

b) Tia ED cắt AB tại F. Chứng minh AC = AF.

c) Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh DI = 2IH.

Lời giải

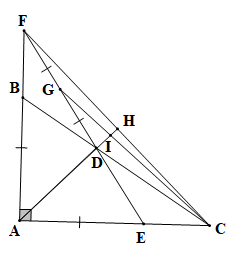
a) Xét $∆$ABD và $∆$EAD có:

AB = AE (giả thiết),

$\widehat{BAD}=\widehat{EAD}$ (do AD là tia phân giác của góc BAC)

AD là cạnh chung

Suy ra ∆ABD = ∆AED (c.g.c)

Do đó $\widehat{ABD}=\widehat{AED}$ (hai góc tương ứng)

Vậy $\widehat{ABD}=\widehat{AED}$.

b) Xét $∆$ABC và $∆$AEF có:

$\widehat{FAC}$ là góc chung,

AB = AE (giả thiết),

$\widehat{ABC}=\widehat{AEF}$ (Do $\widehat{ABD}=\widehat{AED}$)

Suy ra ∆ABC = ∆AEF (g.c.g)

Do đó AC = AF (hai cạnh tương ứng)

Vậy AC = AF.

c) Xét ∆AHF và DAHC có:

AH là cạnh chung,

$\widehat{FAH}=\widehat{CAH}$ (do AD là tia phân giác của góc BAC),

AF = AC (chứng minh câu b)

Do đó ∆AHF = $∆$AHC (c.g.c)

Suy ra HF = HC (hai cạnh tương ứng).

Khi đó H là trung điểm của FC nên DH là đường trung tuyến xuất phát từ đỉnh D của tam giác DFC.

Xét tam giác DFC có CG và DH là hai đường trung tuyến, CG và DH cắt nhau tại I

Suy ra I là trọng tâm của tam giác DFC.

Do đó IH = $\frac{1}{2}$ID (tính chất trọng tâm của tam giác)

Hay DI = 2IH.

Vậy DI = 2IH.