Cho góc nhọn xOy và điểm M nằm trong góc xOy. Gọi E, F là hai điểm nằm ngoài góc xOy
Lời giải Bài 89 trang 94, 95 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 89 trang 94, 95 SBT Toán 7 Tập 2: Cho góc nhọn xOy và điểm M nằm trong góc xOy. Gọi E, F là hai điểm nằm ngoài góc xOy sao cho Ox là đường trung trực của đoạn thẳng ME, Oy là đường trung trực của đoạn thẳng MF (Hình 55).
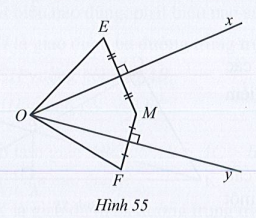
Chứng minh:
a) O là giao điểm ba đường trung trực của tam giác EMF.
b) Nếu thì .
Lời giải
a) Trong tam giác EMF có O là giao điểm hai đường trung trực của ME và MF nên O là giao điểm ba đường trung trực của tam giác EMF.
Vậy O là giao điểm ba đường trung trực của tam giác FEM.
b)
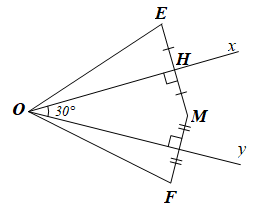
Gọi H là trung điểm của EM.
Xét ∆OEH và ∆OMH có:
,
OH là cạnh chung,
EH = MH (do H là trung điểm của EM).
Do đó ∆OEH = ∆OMH (hai cạnh góc vuông).
Suy ra (hai góc tương ứng).
Do đó Ox là tia phân giác của góc EOM nên
Hay .
Chứng minh tương tự ta cũng có:
Hay .
Ta có
Vậy nếu thì .
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
