Giải sách bài tập Toán 7 Bài 13. Tính chất ba đường cao của tam giác

Bài 92 trang 97 SBT Toán 7 Tập 2: Cho tam giác ABC có AB > AC > BC và H là trực tâm. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

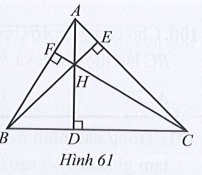
a) H là giao điểm ba đường trung trực của tam giác ABC.

b) CH vuông góc với AB.

c) AH vuông góc với BC.

Lời giải

Vì H là trực tâm của tam giác ABC nên H là giao điểm của ba đường cao trong tam giác ABC.

Do đó phát biểu a là sai.

Vì H là trực tâm của tam giác ABC nên CH ⊥ AB. Do đó phát biểu b là đúng.

Vì H là trực tâm của tam giác ABC nên AH ⊥ BC. Do đó phát biểu c là đúng.

Vậy phát biểu a là sai, phát biểu b và c là đúng.

Bài 93 trang 97 SBT Toán 7 Tập 2: Cho tam giác ABC có AB > AC > BC và K là trực tâm. Trong các phát biểu sau, phát biểu nào đúng?

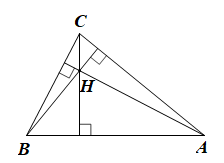
a) K là giao điểm ba đường trung trực của tam giác ABC.

b) K là giao điểm ba đường cao của tam giác ABC.

c) K là giao điểm ba đường phân giác của tam giác ABC.

d) K là giao điểm ba đường trung tuyến của tam giác ABC.

Lời giải

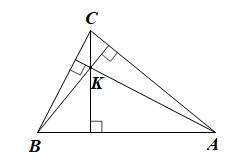
Vì K là trực tâm của tam giác ABC nên K là giao điểm của ba đường cao trong tam giác ABC.

Do đó phát biểu b là đúng.

Vậy ta chọn phát biểu b.

Bài 94 trang 97 SBT Toán 7 Tập 2: Cho tam giác ABC nhọn có các đường cao AD, BE, CF cắt nhau tại H (Hình 61). Tìm trực tâm của các tam giác HAB, HBC, HCA.

Lời giải

• Xét tam giác HAB có BD ⊥ AH, AE ⊥ BH, HF ⊥ AB và ba đường cao BD, AE, HF cắt nhau tại C.

Do đó C là trực tâm tam giác HAB.

• Xét tam giác HBC có HD ⊥ BC, BF ⊥ HC, CE ⊥ BH và ba đường cao HD, BF, CE cắt nhau tại A.

Do đó A là trực tâm tam giác HBC.

• Xét tam giác HCA có HE ⊥ AC, AF ⊥ HC, CD ⊥ AH và ba đường cao HE, AF, CD cắt nhau tại B.

Do đó B là trực tâm tam giác HCA.

Vậy trực tâm của các tam giác HAB, HBC, HCA tương ứng là C, A, B.

Bài 95 trang 97 SBT Toán 7 Tập 2: Cho tam giác ABC có trực tâm H đồng thời cũng là điểm cách đều ba đỉnh của tam giác. Tính số đo các góc của tam giác ABC.

Lời giải

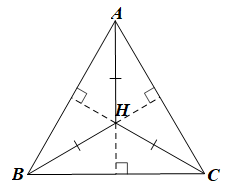
Gọi M là giao điểm của AH và BC.

Vì H cách đều ba đỉnh của tam giác ABC nên HA = HB = HC.

Do HB = HC nên H nằm trên đường trung trực của đoạn thẳng BC.

Tam giác ABC có trực tâm H nên AH ⊥ BC tại M.

Do đó AH là đường trung trực của BC và M là trung điểm của BC.

Khi đó MB = MC.

Xét $∆$ABM và $∆$ACM có:

$\widehat{AMB}=\widehat{AMC}\left(=90°\right)$,

AM là cạnh chung,

MB = MC (chứng minh trên).

Do đó $∆$ABM = $∆$ACM (hai cạnh góc vuông)

Suy ra AB = AC (hai cạnh tương ứng).

Chứng minh tương tự ta cũng có: AB = BC.

Do đó AB = BC = AC nên tam giác ABC là tam giác đều.

Suy ra ba góc của tam giác ABC đều có số đo bằng 60°.

Vậy số đo các góc của tam giác ABC đều bằng 60°.

Bài 96 trang 97 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AB = AD. Vẽ BE vuông góc với CD tại E. Gọi I là giao điểm của AC và BE; K là hình chiếu của I trên BC.

a) Chứng minh ba điểm D, I, K thẳng hàng.

b) Tìm điều kiện của tam giác ABC để I là trọng tâm của tam giác BCD.

Lời giải

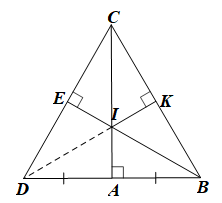
a) Xét tam giác BCD có I là giao điểm của hai đường cao CA và BE nên I là trực tâm của tam giác DBC.

Suy ra DI ⊥ BC.  

Mặt khác, IK ⊥ BC (giả thiết).

Do đó đường cao DI đi qua K nên ba điểm D, I, K thẳng hàng.

Vậy ba điểm D, I, K thẳng hàng.

b) Xét $∆$CDA và $∆$CBA có:

$\widehat{CAD}=\widehat{CAB}\left(={90}^o\right)$,

CA là cạnh chung,

AD = AB (giả thiết)

Do đó $∆$CDA = $∆$CBA (hai cạnh góc vuông)

Suy ra CD = CB (hai cạnh tương ứng) (1)

Tam giác BCD có I là trọng tâm của tam giác nên BE là đường trung tuyến của tam giác.

Do đó CE = DE.

Chứng minh tương tự như trên ta cũng có $∆$BDE = $∆$BCE (hai cạnh góc vuông)

Suy ra BD = BC (hai cạnh tương ứng) (2)

Từ (1) và (2) ta có BC = CD = DB nên tam giác BCD là tam giác đều.

Do đó $\widehat{DBC}=60°$ hay $\widehat{ABC}=60°$

Vậy điều kiện của tam giác ABC để I cũng là trọng tâm của tam giác BCD là tam giác ABC vuông tại A có $\widehat{ABC}=60°$.

Bài 97 trang 97 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A có AB < AC, đường phân giác BD. Vẽ DE vuông góc với BC tại E.

a) Chứng minh trực tâm H của tam giác BAE nằm trên đường thẳng BD.

b) Chứng minh trực tâm của tam giác DAE nằm ngoài tam giác đó.

c) Tìm điều kiện của tam giác ABC để H cách đều các đỉnh của tam giác BAE.

Lời giải

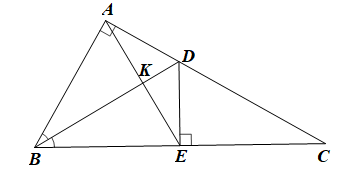
a) Gọi K là giao điểm của BD và AE.

Xét $∆$BAD và $∆$BED có:

$\widehat{BAD}=\widehat{BED}(=90°)$,

BD là cạnh chung,

$\widehat{ABD}=\widehat{EBD}$ (do BD là tia phân giác của góc ABC)

Do đó ∆BAD = ∆BED (cạnh huyền – góc nhọn).

Suy ra BA = BE (hai cạnh tương ứng).

Xét $∆$ABK và $∆$EBK có:

BA = BE (chứng minh trên),

$\widehat{ABK}=\widehat{EBK}$ (do BD là tia phân giác của góc ABC),

BK là cạnh chung

Do đó $∆$ABK = $∆$EBK (c.g.c)

Suy ra $\widehat{BKA}=\widehat{BKE}$ (hai góc tương ứng).

Mà $\widehat{BKA}+\widehat{BKE}=180°$ (hai góc kề bù)

Nên $\widehat{BKA}=\widehat{BKE}=\frac{180°}{2}=90°$

Hay BK ⊥ AE.

Do BK là đường cao của tam giác BAE và B, K, D thẳng hàng nên trực tâm H của tam giác BAE nằm trên đường thẳng BD.

Vậy trực tâm H của tam giác BAE nằm trên đường thẳng BD.

b) Ta có $\widehat{ADE}+\widehat{EDC}=180°$ (hai góc kề bù)

Mà $\widehat{EDC}<90°$ (vì tam giác ECD vuông tại E nên góc EDC là góc nhọn)

Suy ra $\widehat{ADE}>90°$

Do góc ADE là góc tù nên trực tâm của tam giác DAE nằm ngoài tam giác đó.

Vậy trực tâm của tam giác DAE nằm ngoài tam giác đó.

c) Xét tam giác ABE có H là trực tâm, để H cách đều các đỉnh của tam giác BAE thì tam giác BAE là tam giác đều (theo kết quả của Bài tập 95, trang 97, Sách Bài tập Toán 7, Tập hai).

Do đó $\widehat{ABE}=60°$ hay $\widehat{ABC}=60°$.

Vậy điều kiện để H cách đều các đỉnh của tam giác BAE là tam giác ABC vuông tại A có $\widehat{ABC}=60°$.

Bài 98 trang 97, 98 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A, đường trung tuyến AM. Từ M kẻ ME vuông góc với AB (E ∈ AB), kẻ MF vuông góc với AC (F ∈ AC). Gọi I là giao điểm của AM và EF. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh:

a) AM vuông góc với EF;

b) Trực tâm của các tam giác ABD và ACD nằm trên đường thẳng BC;

c) Trực tâm của các tam giác AEF, MEF, DBC và ABC nằm trên cùng một đường thẳng.

Lời giải

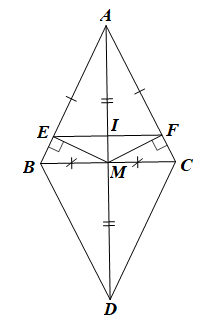
a) Vì tam giác ABC cân tại A nên AB = AC, $\widehat{ABC}=\widehat{ACB}$.

Xét $∆$BME và $∆$CMF có:

$\widehat{BEM}=\widehat{CFM}(=90°)$,

BM = CM (vì M là trung điểm của BC),

$\widehat{ABC}=\widehat{ACB}$ (chứng minh trên)

Do đó ∆BME = ∆CMF (cạnh huyền – góc nhọn)

Suy ra ME = MF, BE = CF (các cặp cạnh tương ứng).

Ta có ME = MF nên M nằm trên đường trung trực của đoạn thẳng EF (1)

Lại có AB = AE + EB, AC = AF + FC

Mà AB = AC, BE = CF (chứng minh trên)

Suy ra AE = AF nên A nằm trên đường trung trực của đoạn thẳng EF (2)

Từ (1) và (2) suy ra AM là đường trung trực của đoạn thẳng EF.

Do đó AM vuông góc với EF.

Vậy AM vuông góc với EF.

b) Xét $∆$ABM và $∆$ACM có:

AB = AC, BM = CM, AM là cạnh chung

Do đó $∆$ABM = $∆$ACM (c.c.c)

Suy ra $\widehat{AMB}=\widehat{AMC}$ (hai góc tương ứng).

Mà $\widehat{AMB}+\widehat{AMC}=180°$ (hai góc kề bù)

Do đó $\widehat{AMB}=\widehat{AMC}=\frac{180°}{2}=90°$

Suy ra AM ⊥ BC hay BM ⊥ AD và CM ⊥ AD .

Mà BM và CM là các đường cao tương ứng của các tam giác ABD, ACD.

Suy ra trực tâm của các tam giác ABD và ACD nằm trên đường thẳng BC.

Vậy trực tâm của các tam giác ABD và ACD nằm trên đường thẳng BC.

c) Ta có AM là đường trung trực của đoạn thẳng EF nên AM ⊥ EF.

Do đó trực tâm của tam giác AEF và tam giác MEF nằm trên đường thăng AM hay chính là đường thẳng AD.

Xét tam giác ABC có AM là đường cao nên trực tâm tam giác ABC nằm trên đường thẳng AM hay chính là đường thẳng AD.

Xét tam giác DBC có DM là đường cao nên trực tâm tam giác DBC nằm trên đường thẳng DM hay chính là đường thẳng AD.

Suy ra trực tâm của các tam giác AEF, MEF, DBC và ABC nằm trên đường thẳng AD.

Vậy trực tâm của các tam giác AEF, MEF, DBC và ABC nằm trên cùng một đường thẳng, đó là đường thẳng AD.