Cho hai tam giác đều chung đáy ABC và BCD. Gọi I là trung điểm của BC
Lời giải Bài 85 trang 94 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Giải SBT Toán 7 Cánh diều Bài 12. Tính chất ba đường trung trực của tam giác
Bài 85 trang 94 SBT Toán 7 Tập 2: Cho hai tam giác đều chung đáy ABC và BCD. Gọi I là trung điểm của BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Đường thẳng BC là đường trung trực của AD.
b) Điểm I cách đều các điểm A, B, D.
c) Điểm B nằm trên đường trung trực của CD.
d) Điểm C không nằm trên đường trung trực của BD.
Lời giải
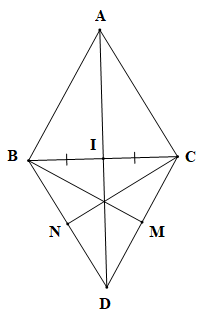
Vì tam giác ABC, DBC là tam giác đều nên AB = AC = BC = BD = DC.
• Ta có CA = CD nên C nằm trên đường trung trực của đoạn thẳng AD.
Do BA = BD nên B nằm trên đường trung trực của đoạn thẳng AD.
Suy ra BC là đường trung trực của đoạn thẳng AD.
Do đó phát biểu a là đúng.
• Vì BC = BD nên điểm B nằm trên đường trung trực của CD.
Do đó phát biểu c là đúng.
• Vì CB = CD nên điểm C nằm trên đường trung trực của BD.
Do đó phát biểu d là sai.
• Tam giác ABC là tam giác đều nên .
Trong tam giác ABI vuông tại I có (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra .
Xét tam giác ABI có (do 60° > 30°).
Suy ra AI > BI (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)
Do đó điểm I không cách đều hai điểm A và B nên phát biểu b là sai.
Vậy phát biểu a, c là đúng; phát biểu b, d là sai.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
