Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC
Lời giải Bài 106 trang 99 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 106 trang 99 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.
a) Chứng minh .
b) Tia ED cắt AB tại F. Chứng minh AC = AF.
c) Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh DI = 2IH.
Lời giải
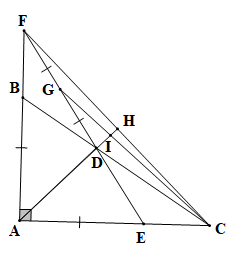
a) Xét ABD và EAD có:
AB = AE (giả thiết),
(do AD là tia phân giác của góc BAC)
AD là cạnh chung
Suy ra ∆ABD = ∆AED (c.g.c)
Do đó (hai góc tương ứng)
Vậy .
b) Xét ABC và AEF có:
là góc chung,
AB = AE (giả thiết),
(Do )
Suy ra ∆ABC = ∆AEF (g.c.g)
Do đó AC = AF (hai cạnh tương ứng)
Vậy AC = AF.
c) Xét ∆AHF và DAHC có:
AH là cạnh chung,
(do AD là tia phân giác của góc BAC),
AF = AC (chứng minh câu b)
Do đó ∆AHF = AHC (c.g.c)
Suy ra HF = HC (hai cạnh tương ứng).
Khi đó H là trung điểm của FC nên DH là đường trung tuyến xuất phát từ đỉnh D của tam giác DFC.
Xét tam giác DFC có CG và DH là hai đường trung tuyến, CG và DH cắt nhau tại I
Suy ra I là trọng tâm của tam giác DFC.
Do đó IH = ID (tính chất trọng tâm của tam giác)
Hay DI = 2IH.
Vậy DI = 2IH.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
