Cho tam giác ABC có ba góc nhọn, AB < AC < BC
Lời giải Bài 103 trang 98 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
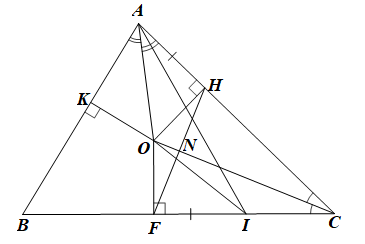
Bài 103 trang 98 SBT Toán 7 Tập 2: Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC; H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Chứng minh:
a) OC vuông góc với FH;
b) Tam giác OAI là tam giác cân;
c) Tam giác BAI là tam giác cân.
Lời giải
a) Xét OHC và OFC có:
,
OC là cạnh chung,
(do CO là tia phân giác của góc ACB)
Do đó ∆OHC = ∆OFC (cạnh huyền – góc nhọn)
suy ra CH = CF, OH = OF (các cặp cạnh tương ứng).
Do đó C và O cùng nằm trên đường trung trực của đoạn thẳng FH.
Hay CO là đường trung trực của đoạn thẳng FH.
Do đó OC ⊥ FH.
Vậy OC ⊥ FH.
b) Xét ∆OHA và ∆OFI có:
,
OH = OF (chứng minh câu a),
AH = IF (giả thiết),
Do đó ∆OHA = ∆OFI (hai cạnh góc vuông)
Suy ra OA = OI (hai cạnh tương ứng)
Tam giác OAI có OA = OI nên ∆OAI cân tại O.
Vậy tam giác OAI là tam giác cân tại O.
c) • Kẻ OK ⊥ AB (K ∈ AB).
Xét AOH và AOK có
,
OA là cạnh chung,
(do AO là tia phân giác của góc BAC)
Do đó ∆AOH = ∆AOK (cạnh huyền – góc nhọn)
Suy ra AH = AK (hai cạnh tương ứng).
• Xét tam giác ABC có O là giao điểm của hai tia phân giác của góc ACB và BAC.
Suy ra BO là tia phân giác của góc ABC.
Xét BOK và BOF có
,
OB là cạnh chung,
(do BO là tia phân giác của góc ABC)
Do đó ∆BOK = ∆BOF (cạnh huyền – góc nhọn).
Suy ra BK = BF (hai cạnh tương ứng)
• Ta có AB = AK + KB, BI = BF + FI
Mà BK = BF, AK = IF (= AH)
Từ đó suy ra AB = BI nên tam giác BAI cân tại B.
Vậy tam giác BAI cân tại B.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
