Cho tam giác ABC có góc BAC bằng 110 độ
Lời giải Bài 100 trang 98 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Giải SBT Toán 7 Cánh diều Bài tập cuối chương 7
Bài 100 trang 98 SBT Toán 7 Tập 2: Cho tam giác ABC có . Các đường trung trực của AB và AC cắt cạnh BC lần lượt tại E và F. Khi đó, số đo góc EAF bằng:
A. 20°;
B. 30°;
C. 40°;
D. 50°.
Lời giải
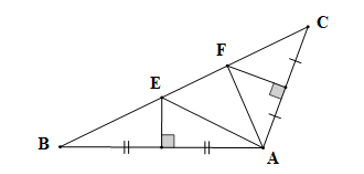
Xét tam giác ABC có:
(tổng ba góc trong một tam giác)
Suy ra .
Vì E thuộc đường trung trực của AB nên EB = EA.
Do đó tam giác ABE cân tại E nên .
Vì F thuộc đường trung trực của AC nên FC = FA.
Do đó tam giác ACF cân tại F nên .
Ta có
Hay
Do đó
Suy ra .
Vậy ta chọn đáp án C.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
