Cho hai tam giác ABC và MNP có góc ABC bằng góc MNP
Lời giải Bài 99 trang 98 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Giải SBT Toán 7 Cánh diều Bài tập cuối chương 7
Bài 99 trang 98 SBT Toán 7 Tập 2:
Cho hai tam giác ABC và MNP có Cần thêm một điều kiện để tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc – cạnh – góc là:
A. AC = MP;
B. AB = MN;
C. BC = NP;
D. AC = MN.
Lời giải
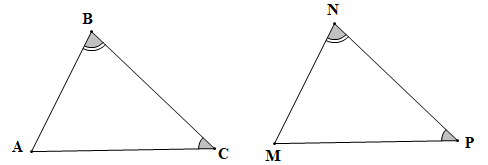
Để ΔABC = ∆MNP theo trường hợp góc – cạnh – góc thì hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh bằng nhau của hai tam giác.
Mà
Lại có và là hai góc kề cạnh BC;
và là hai góc kề cạnh NP.
Do đó điều kiện còn thiếu là điều kiện về cạnh, đó là BC = NP.
Vậy ta chọn đáp án C.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
