Cho tam giác ABC có góc ABC bằng 53 độ , góc BAC bằng 90 độ
Lời giải Bài 35 trang 78 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
a) Chứng minh ∆AHB = ∆DBH.
b) Chứng minh DH vuông góc với AC.
c) Tính số đo góc BDH.
Lời giải
a) Xét ∆AHB và ∆DBH có:
(cùng bằng 90°),
BH là cạnh chung,
AH = BD (giả thiết),
Suy ra ∆AHB = ∆DBH (hai cạnh góc vuông).
Vậy ∆AHB = ∆DBH.
b) Do ∆AHB = ∆DBH (chứng minh câu a) nên (hai góc tương ứng).
Mà ở vị trí so le trong
Do đó AB // DH.
Lại có, AB ⊥ AC nên DH ⊥ AC (một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại).
Vậy DH ⊥ AC.
c) Do ∆AHB = ∆DBH (chứng minh câu a) nên (hai góc tương ứng).
Xét tam giác ABH vuông tại H có:
(trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra .
Do đó .
Vậy .
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài 31 trang 77 SBT Toán 7 Tập 2: Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC. Trong các phát biểu sau, phát biểu nào sai? Vì sao?...
Bài 32 trang 78 SBT Toán 7 Tập 2: Nêu thêm một điều kiện để hai tam giác trong mỗi hình 22a, 22b, 22c, 22d là hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh...
Bài 33 trang 78 SBT Toán 7 Tập 2: Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE...
Bài 34 trang 78 SBT Toán 7 Tập 2: Cho điểm M nằm giữa hai điểm O và A. Vẽ các điểm N và B sao cho O là trung điểm của AB và MN. Vẽ tia Ox vuông góc với AB, trên tia Ox lấy điểm K. Chứng minh...
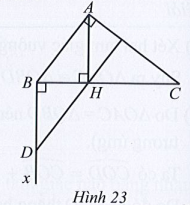
Bài 35 trang 78 SBT Toán 7 Tập 2: Cho tam giác ABC có , AH vuông góc với BC (H thuộc BC). Vẽ tia Bx vuông góc với BC. Trên tia Bx lấy điểm D sao cho BD = HA (Hình 23)...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
