Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB

Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC

Lời giải Bài 31 trang 77 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

166

« Trang trước

Trang sau »

Giải SBT Toán 7 Cánh diều Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 31 trang 77 SBT Toán 7 Tập 2: Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC. Trong các phát biểu sau, phát biểu nào sai? Vì sao?

a) ΔAED = ΔACB. b) DE = BC.

c) ΔACE = ΔABD. d) $\hat{A B C} = \hat{A ED}$ .

Lời giải

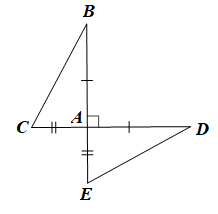
Sách bài tập Toán 7 Bài 5 (Cánh diều): Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (ảnh 1)

Xét ΔAED và ΔACB có:

$\hat{D A E} = \hat{B A C}$ (cùng bằng 90°),

AD = AB (giả thiết),

AE = AC (giả thiết)

Do đó ΔAED = ΔACB (hai cạnh góc vuông) nên phát biểu a đúng.

Từ ΔAED = ΔACB, suy ra:

• DE = BC (hai cạnh tương ứng), nên phát biểu b đúng.

• $\hat{A B C} = \hat{A DE}$ (hai góc tương ứng) nên phát biểu d sai.

Xét $∆$ ACE và $∆$ ABD, ta thấy hai tam giác này không có các cạnh bằng nhau, các góc bằng nhau. Do đó hai tam giác này không bằng nhau, nên phát biểu c sai.

Vậy phát biểu c, d là phát biểu sai.

Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:

Bài 31 trang 77 SBT Toán 7 Tập 2: Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC. Trong các phát biểu sau, phát biểu nào sai? Vì sao?...

Bài 32 trang 78 SBT Toán 7 Tập 2: Nêu thêm một điều kiện để hai tam giác trong mỗi hình 22a, 22b, 22c, 22d là hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh...