Cho tam giác ABC, tia phân giác của góc BAC cắt cạnh BC tại D
Lời giải Bài 9 trang 69 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 9 trang 69 SBT Toán 7 Tập 2: Cho tam giác ABC, tia phân giác của ^BAC cắt cạnh BC tại D. Tính số đo mỗi góc của tam giác ABC, biết ^ADB=80° và ˆB=1,5ˆC.
Lời giải
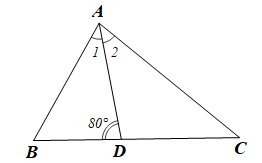
• Xét ∆ABD có: ˆA1+ˆB+^ADB=180° (tổng ba góc của một tam giác)
Suy ra ˆA1+ˆB=180°−^ADB=180°−80°=100°
Khi đó ˆA1=100°−ˆB
Lại có ˆB=1,5ˆC
Suy ra ˆA1=100°−1,5ˆC (1)
• Vì ^ADB là góc ngoài của tam giác ACD tại đỉnh D nên ^ADB=ˆC+ˆA2
Suy ra ˆA2=^ADB−ˆC=80o−ˆC (2)
• Ta có AD là tia phân giác của góc BAC nên ˆA1=ˆA2 (3)
Từ (1), (2), (3) ta có: 100°−1,5ˆC=80°−ˆC
Hay 1,5ˆC−ˆC=100°−80°
Suy ra ˆC=40°.
Do đó ˆB=1,5ˆC=1,5.40°=60°.
Xét ∆ABC có: ˆC+ˆB+^BAC=180° (tổng ba góc của một tam giác).
Do đó ^BAC=180°−ˆC−ˆB=180°−40°−60°=80°.
Vậy ˆC=40°, ˆB=60°, ^BAC=80°.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài 1 trang 68 SBT Toán 7 Tập 2: Cho tam giác MHK vuông tại H. Ta có: A. ˆM+ˆK>90°;B. ˆM+ˆK=90°...
Bài 2 trang 68 SBT Toán 7 Tập 2: Quan sát Hình 3. a) Tính các số đo x, y, z. b) Hãy nhận xét về tổng các số đo x + y + z...
Bài 3 trang 68 SBT Toán 7 Tập 2: a) Cho biết một góc nhọn của tam giác vuông bằng 40°. Tính số đo góc nhọn còn lại...
Bài 6 trang 68 SBT Toán 7 Tập 2: Tính số đo các góc của tam giác ABC trong mỗi trường hợp sau: a) ˆA=ˆB=ˆC; b) ˆA=70° và ˆC−ˆB=20°...
