Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H
Lời giải Bài 7 trang 68 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 7 trang 68 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H, AD là tia phân giác của (Hình 4)
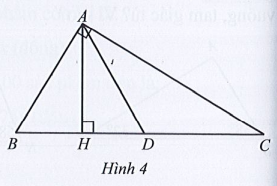
a) Tìm các cặp góc có tổng số đo bằng 90°.
b) Cho . Tính số đo của
c) Chứng minh:
Lời giải
a) Xét ABC vuông tại A ta có:
(trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Xét ABH vuông tại H ta có:
(trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Xét ACH vuông tại H ta có:
(trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Xét ADH vuông tại H ta có:
(trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Ta có:
Vậy các cặp góc có tổng số đo bằng 90° là:
và ; và ; và ; và ; và ; và .
b) • Do (chứng minh câu a) nên .
Mà nên .
• Do (chứng minh câu a)
Nên .
Mà AD là tia phân giác của (giả thiết)
Do đó .
• Do (chứng minh câu a)
Nên hay
Vậy
c) Vì (chứng minh câu a)
Nên .
Khi đó , .
Lại có (chứng minh câu a)
Mà suy ra hày
Vậy
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài 1 trang 68 SBT Toán 7 Tập 2: Cho tam giác MHK vuông tại H. Ta có: A. ;B. ...
Bài 2 trang 68 SBT Toán 7 Tập 2: Quan sát Hình 3. a) Tính các số đo x, y, z. b) Hãy nhận xét về tổng các số đo x + y + z...
Bài 3 trang 68 SBT Toán 7 Tập 2: a) Cho biết một góc nhọn của tam giác vuông bằng 40°. Tính số đo góc nhọn còn lại...
Bài 6 trang 68 SBT Toán 7 Tập 2: Tính số đo các góc của tam giác ABC trong mỗi trường hợp sau: a) ; b) và ...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
