Giải bài tập Toán 10 Bài 1: Hàm số và đồ thị

Video giải bài tập Toán 10 Bài 1: Hàm số và đồ thị 

Câu hỏi khởi động

Khởi động trang 31 Toán lớp 10 Tập 1: Làm thế nào để mô tả được mối liên hệ giữa thời gian t và quãng đường đi được S của vật rơi tự do? Làm thế nào để có được hình ảnh hình học minh họa mối liên hệ giữa hai đại lượng đó?

Lời giải:

Theo công thức rơi tự do được tìm hiểu ở Vật lý 10, ta có:

Công thức tính quãng đường S (m) của vật rơi tự do theo thời gian t (s) là: S = $\frac{1}{2}$gt², trong đó g là gia tốc rơi tự do, g ≈ 9,8 m/s².

Để có được hình hẻnh hình học minh họa về mối liên hệ đó ta cần vẽ đồ thị hàm số S = $\frac{1}{2}$gt² trên hệ trục tọa độ.

1. Hàm số

Hoạt động 1 trang 31 Toán lớp 10 Tập 1: Trong bài toán ở phần mở đầu, ta đã biết công thức tính quãng đường đi được S (m) của vật rơi tự do theo thời gian t(s) là

S = $\frac{1}{2}$gt², trong đó g là gia tốc rơi tự do, g ≈ 9,8 m/s².

a) Với mỗi giá trị t = 1, t = 2, tính giá trị tương ứng của S.

b) Với mỗi giá trị của t có bao nhiêu giá trị tương ứng của S?

Lời giải:

Ta có g ≈ 9,8 m/s²  nên S = $\frac{1}{2}$gt² =$\frac{1}{2}.9,8t^2=4,9t^2\left(1\right).$

a) Thay t = 1 vào biểu thức (1) ta có: S = 4,9 . 1² = 4,9 (m).

Thay t = 2 vào biểu thức (1) ta có: S = 4,9 . 2² = 19,6 (m).

Vậy với t = 1s thì S = 4,9 m và t = 2s thì S = 19,6 m.

b) Tương ứng với mỗi giá trị của t ta sẽ tính được một giá trị S.

Hoạt động 2 trang 31, 32 Toán lớp 10 Tập 1: Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệp tính toán lợi nhuận y (đồng) theo công thức sau: y = – 200x² + 92 000x – 8 400 000, trong đó x là số sản phẩm loại đó được bán ra.

a) Với mỗi giá trị x = 100, x = 200, tính giá trị tương ứng của y. 

b) Với mỗi giá trị của x có bao nhiêu giá trị tương ứng của y? 

Lời giải:

a) Thay x = 100 vào công thức đã cho, ta được: y = – 200 . 100² + 92 000 . 100 – 8 400 000 = – 1 200 000.

Thay x = 200 vào công thức đã cho, ta được: y = – 200 . 200² + 92 000 . 200 – 8 400 000 = 2 000 000.

Vậy với x = 100 thì y = – 1 200 000 và với x = 200 thì y = 2 000 000.

b) Ta thấy với mỗi giá trị x sẽ tìm được một giá trị y tương ứng.

Luyện tập 1 trang 32 Toán lớp 10 Tập 1: Trong y học một người cân nặng 60kg chạy với tốc độ 6,5 km /h thì lượng ca-lo tiêu thụ được tính theo công thức: c = 4,7t (Nguồn: https://icarre.vn), trong đó thời gian t được tính theo phút. Hỏi c có phải là hàm số của t không? Vì sao?

Lời giải:

c = 4,7t là một hàm số của biến số t vì với mỗi giá trị t (phút) có một và chỉ một giá trị tương ứng của c.

Hoạt động 3 trang 32 Toán lớp 10 Tập 1: Cho hai hàm số y = 2x + 1 (1) và $y=\sqrt{x-2}$ (2).

a) Nêu biểu thức xác định mỗi hàm số trên. 

b) Tìm x sao cho mỗi biểu thức trên có nghĩa. 

Lời giải:

a) Biểu thức xác định hàm số (1) là 2x + 1.

Biểu thức xác định hàm số (2) là $\sqrt{x-2}$.

b) Biểu thức 2x + 1 có nghĩa với mọi $x\in ℝ$.

Biểu thức $\sqrt{x-2}$ có nghĩa khi x – 2 ≥ 0 ⇔ x ≥ 2.

Vậy biểu thức 2x + 1 có nghĩa với mọi $x\in ℝ$ và biểu thức $\sqrt{x-2}$ có nghĩa khi x ≥ 2.

Luyện tập 2 trang 32 Toán lớp 10 Tập 1: Tìm tập xác định của hàm số:

$y=\frac{\sqrt{x+2}}{x-3}$

Lời giải:

Hàm số $y=\frac{\sqrt{x+2}}{x-3}$ xác định khi biểu thức $\frac{\sqrt{x+2}}{x-3}$ có nghĩa khi

⇔$\left\{\begin{array}{l}x+2\ge 0\\ x-3\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x\ge -2\\ x\ne 3\end{array}\right.$.

Suy ra tập xác định của hàm số đã cho là D = {$x\in ℝ|$x ≥ – 2, x ≠ 3} hay D = $\left[-2;+\infty \right)\backslash 3$.

Vậy tập xác định của hàm số đã cho là D = {$x\in ℝ|$x ≥ – 2, x ≠ 3} = $\left[-2;+\infty \right)\backslash 3$.

Luyện tập 3 trang 33 Toán lớp 10 Tập 1: Cho hàm số:

$y=\left\{\begin{array}{l}-xn{ê}^{\text{'}}ux<0\\ xn{ê}^{\text{'}}ux>0.\end{array}\right.$

a) Tìm tập xác định của hàm số trên. 

b) Tính giá trị của hàm số khi x = – 1; x = 2 022. 

Lời giải:

a) Hàm số đã cho xác định khi x < 0, x > 0 nên tập xác định của hàm số là D = $ℝ\backslash \left\{0\right\}$.

Vậy tập xác định của hàm số đã cho là D = $ℝ\backslash \left\{0\right\}$.

b) Với x = – 1 < 0 ta thay x  = -1 vào hàm số y = -x, ta được: y = – (– 1) = 1.

Với x = 2 022 > 0 ta thay x = 2 022 vào hàm số y = x, ta được: y = x = 2 022.

Vậy giá trị của hàm số đã cho tại x = – 1 là y = 1, tại x = 2 022 là y = 2 022.

Hoạt động 4 trang 34 Toán lớp 10 Tập 1: Xét hàm số y = f(x) = x².

a) Tính các giá trị y₁ = f(x₁), y₂ = f(x₂) tương ứng với giá trị x₁ = – 1, x₂ = 1. 

b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm M₁(x₁; y_1­), M₂(x₂; y₂). 

Lời giải:

a) Thay x₁ = -1 vào hàm số y = f(x) = x², ta được:

y₁ = f(x₁) = f(– 1) = (– 1)² = 1.

Thay x₂ = -1 vào hàm số y = f(x) = x², ta được:

y₂ = f(x₂) = f(1) = 1² = 1.

Vậy tương ứng với giá trị x₁ = – 1, x₂ = 1 thì các giá trị y₁ = f(x₁) = 1, y₂ = f(x₂) = 1.

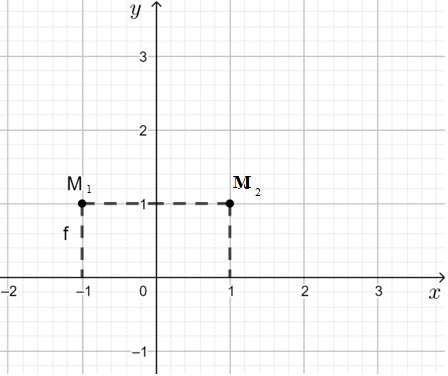
b) Với x₁ = - 1 thì y₁ = f(x₁) = 1 nên điểm: M₁(– 1; 1)

Với x₁ = 1 thì y₁ = f(x₁) = 1 nên điểm: M­₂(1; 1).

Ta hai điểm M₁ và M₂  biểu diễn lên mặt phẳng tọa độ Oxy như sau:

2. Đồ thị của hàm số

Luyện tập 4 trang 34 Toán lớp 10 Tập 1: Cho hàm số $y=\frac{1}{x}$ và ba điểm M(– 1; – 1), N(0; 2), P(2; 1). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?

Lời giải:

Hàm số $y=\frac{1}{x}$ có nghĩa khi x ≠ 0.

+ Điểm M(– 1; – 1)

Thay x = -1 và y = - 1 vào đồ thị hàm số ta được y = $–1=\frac{1}{-1}$ (luôn đúng).

Suy ra điểm M thuộc vào đồ thị hàm số đã cho.

+ Điểm N(0; 2)

Điểm N có hoành độ x = 0 mà hàm số có nghĩa khi x ≠ 0 nên điểm N không thuộc vào đồ thị hàm số đã cho.

+ Điểm P(2; 1)

Thay x = 2 và y = 1 vào đồ thị hàm số đã cho ta được: $1=\frac{1}{2}$ (vô lý)

Suy ra điểm P không thuộc đồ thị hàm số $y=\frac{1}{x}$.

Vậy có điểm M thuộc đồ thị hàm số đã cho và điểm N và P là hai điểm không thuộc đồ thị hàm số đã cho.

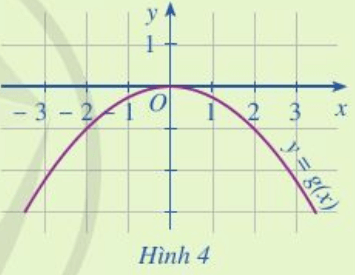
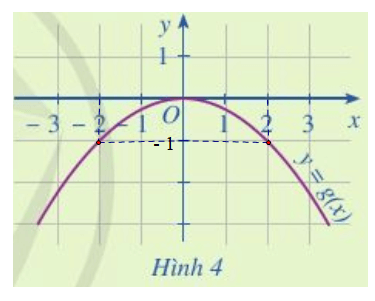
Luyện tập 5 trang 35 Toán lớp 10 Tập 1: Dựa vào Hình 4, xác định g(– 2), g(0), g(2).

Lời giải:

Ta có: g(– 2) là giá trị của hàm số tại x = – 2,

g(0) là giá trị của hàm số tại x = 0,

g(2) là giá trị của hàm số tại x = 2.

Để xác định g(-2), g(0) và g(2) ta làm như sau:

Tại điểm x = -2 dóng một đường thẳng đứng vuông góc đường thẳng này cắt đồ thị hàm số tại điểm có tọa độ (-2; -1) nên g(-2) = - 1 (như trên hình vẽ).

Tại điểm x = 0 dóng một đường thẳng đứng vuông góc đường thẳng này cắt đồ thị hàm số tại điểm O(0; 0) nên g(0) = 0 (như trên hình vẽ).

Tại điểm x = 2 dóng một đường thẳng đứng vuông góc đường thẳng này cắt đồ thị hàm số tại điểm có tọa độ (2; -1) nên g(2) = -1 (như trên hình vẽ).

Vậy g(– 2) = – 1, g(0) = 0, g(2) = – 1.

3. Sự biến thiên của hàm số

Hoạt động 5 trang 36 Toán lớp 10 Tập 1: Cho hàm số f(x) = x + 1.

a) So sánh f(1) và f(2).

b) Chứng minh rằng nếu $x_1,x_2\in ℝ$ sao cho x₁ < x₂ thì f(x₁) < f(x₂).

Lời giải:

a) Ta có f(1) và f(2) lần lượt là giá trị của hàm số tại điểm x = -1 và x = 2, khi đó:

f(1) = 1 + 1 = 2, f(2) = 2 + 1 = 3.

Vì 2 < 3 nên f(1) < f(2).

Vậy f(1) < f(2).

b) Ta có f(x₁) và f(x₂) lần lượt là các giá trị của hàm số tại x₁ và x₂, khi đó f(x₁) = x₁ + 1, f(x₂) = x₂ + 1

Vì x₁ < x₂ nên x₁ + 1 < x₂ + 1

Do đó: f(x₁) < f(x₂) với mọi $x_1,x_2\in ℝ$.

Vậy f(x₁) < f(x₂) với mọi $x_1,x_2\in ℝ$ thỏa mãn x₁ < x₂.

Luyện tập 6 trang 36 Toán lớp 10 Tập 1: Chứng tỏ rằng hàm số y = 6x² nghịch biến trên khoảng (– ∞; 0).

Lời giải:

Với x $\in$ (– ∞; 0) thì y = 6x² luôn xác định.

Xét hai số bất kì x₁, x₂ ∈ (– ∞; 0) sao cho x₁ < x₂.

Khi đó, ta có: x₁ < x₂ < 0 nên $x_1^2>x_2^2\iff 6x_1^2>6x_2^2$ hay f(x₁) > f(x₂).

Vậy hàm số nghịch biến trên khoảng (– ∞; 0).

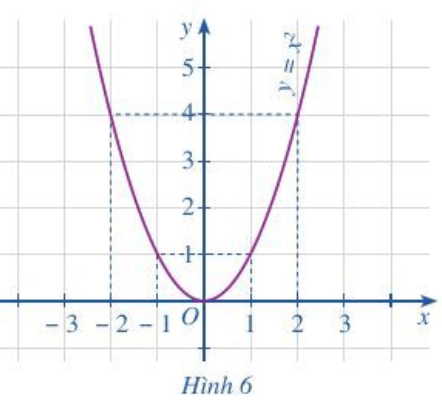
Hoạt động 6 trang 36, 37 Toán lớp 10 Tập 1: Cho đồ thị hàm số: y = f(x) = x² như Hình 6.

a) So sánh f(– 2), f(– 1). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ – 2 đến – 1. 

b) So sánh f(1), f(2). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ 1 đến 2. 

Lời giải:

a) Tại điểm x = -2 trên trục hoành dóng một đường thẳng đứng vuông góc với trục Ox cắt đồ thị tại điểm có tọa độ (-2; 4) nên f(-2) = 4.

Tại điểm x = -1 dóng một đường thẳng vuông góc với trục Ox cắt đồ thị tại điểm có tọa độ (-1; 1) nên f(-1) = 1.

Vì 4 > 1 nên f(– 2) > f(– 1).

Nhận xét về sự biến thiên của giá trị hàm số:

Khi giá trị biến x tăng dần từ – 2 đến – 1 thì giá trị của hàm số giảm dần từ 4 xuống 1.

b) Tại điểm x = 1 trên trục hoành dóng một đường thẳng đứng vuông góc với trục Ox cắt đồ thị tại điểm có tọa độ (1; 1) nên f(1) = 1.

Tại điểm x = 2 dóng một đường thẳng vuông góc với trục Ox cắt đồ thị tại điểm có tọa độ (2; 4) nên f(2) = 4.

Vì 1 < 4 nên f(1) < f(2).

Nhận xét về sự biến thiên của giá trị hàm số:

Khi giá trị biến x tăng dần từ 1 đến 2 thì giá trị của hàm số tăng dần từ 1 lên 4.

Bài tập

Bài 1 trang 37 Toán lớp 10 Tập 1: Tìm tập xác định của mỗi hàm số sau:

a) y = – x²;

b) $y=\sqrt{2-3x}$;

c) $y=\frac{4}{x+1}$;

d) $y=\left\{\begin{array}{l}1n{ê}^{\text{'}}ux\in \mathbb{Q}\\ 0n{ê}^{\text{'}}ux\in ℝ\backslash \mathbb{Q}.\end{array}\right.$

Lời giải:

a) Hàm số y = – x² xác định với mọi $x\in ℝ$.

Do đó tập xác định D = $ℝ$.

Vậy tập xác định của hàm số là D = $ℝ$.

b) Biểu thức $\sqrt{2-3x}$ có nghĩa khi 2 – 3x ≥ 0 $\iff -3x\ge -2\iff x\le \frac{2}{3}$.

Do đó tập xác định D = {x $\in ℝ$| $x\le \frac{2}{3}$} = $\left(-\infty ;\frac{2}{3}\right]$.

Vậy tập xác định của hàm số là D = $\left(-\infty ;\frac{2}{3}\right]$.

c) Biểu thức $\frac{4}{x+1}$ xác định khi x + 1 ≠ 0 ⇔ x ≠ – 1.

Suy ra tập xác định của hàm số là D = {x$\in ℝ$| x ≠ – 1} = $ℝ\backslash \left\{-1\right\}$.

Vậy tập xác định của hàm số là D = $ℝ\backslash \left\{-1\right\}$.

d)

Ta có:

Hàm số bằng 1 nếu $x\in \mathbb{Q}$

Hàm số bằng 0 nếu $x\in ℝ\backslash \mathbb{Q}$

Do đó hàm có nghĩa khi $x\in \mathbb{Q}$ hoặc $x\in ℝ\backslash \mathbb{Q}$ hay  $x\in \mathbb{Q}\cup \left(ℝ\backslash \mathbb{Q}\right)=ℝ$.

Vậy tập xác định của hàm số là D = $ℝ$.

Bài 2 trang 37, 38 Toán lớp 10 Tập 1: Bảng 1 dưới đây cho biết chỉ số PM_2,5 (bụi mịn) ở Thành phố Hà Nội từ tháng 1 đến tháng 12 của năm 2019

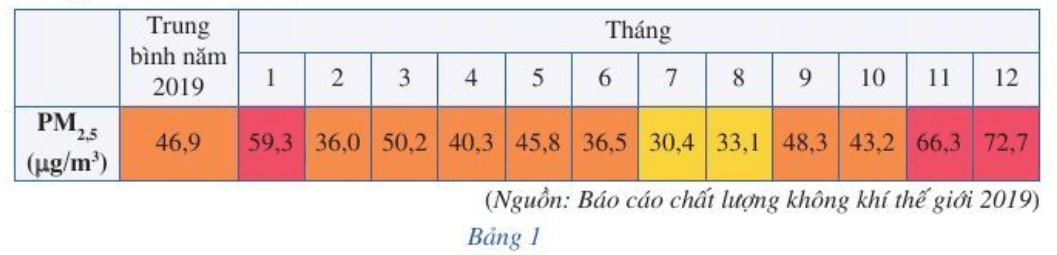
a) Nêu chỉ số PM_2,5 trong tháng 2; tháng 5; tháng 10. 

b) Chỉ số PM_2,5 có phải là hàm số của tháng không? Tại sao?

c) Bụi mịn PM2,5 có đường kính nhỏ hơn 2,5 μm (mi-crô-mét) dễ dàng xâm nhập vào cơ thể con người thông qua đường hô hấp và gây nên một số bệnh nguy hiểm như đột quỵ, tim mạch,.. Em hãy nêu một số biện pháp bảo vệ bản thân trước bụi mịn.

Lời giải:

a) Quan sát bảng ta thấy chỉ số PM2,5 trong tháng 2 là 36,0 μg/m3; trong tháng 5 là 45,8 μg/m3; trong tháng 10 là 43,2 μg/m3. 

b) Chỉ số PM2,5 là hàm số của tháng vì mỗi tháng chỉ tương ứng với đúng một giá trị của chỉ số PM2,5. 

c) Một số biện pháp bảo vệ bản thân trước bụi mịn: 

- Dọn dẹp vệ sinh nơi ở, nếu có điều kiện nên sử dụng máy lọc không khí trong nhà. 

- Sử dụng khẩu trang thích hợp khi đi ra ngoài. 

- Tạo ra thoái quen sinh hoạt tốt cho sức khỏe: Vệ sinh mũi họng, ăn uống lành mạnh, đủ chất, uống nhiều nước, tránh tiếp xúc với môi trường bụi bẩn,…

Bài 3 trang 38 Toán lớp 10 Tập 1: Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250 g như trong bảng sau:

a) Số tiền dịch vụ thư cơ bản phải trả y (đồng) có là hàm số của khối lượng thư cơ bản x (g) hay không? Nếu đúng, hãy xác định những công thức tính y. 

b) Tính số tiền phải trả khi bạn Dương gửi thư có khối lượng 150g, 200g. 

Lời giải:

 a) Quan sát bảng số liệu, ta thấy: Với mỗi khối lượng thư cơ bản x (g) có một và chỉ một mức cước tương ứng hay số tiền dịch vụ cơ bản phải trả y (đồng) tương ứng nên y là hàm số của x.

Ta có:

+ Nếu 0 < x ≤ 20 thì y = 4 000.

+ Nếu 20 < x ≤ 100 thì y = 6 000.

+ Nếu 100 < x ≤ 250 thì y = 8 000.

Khi đó, ta có công thức xác định y như sau: 

$y=\left\{\begin{array}{l}4000n{ê}^{\text{'}}u0<x\le 20\\ 6000n{ê}^{\text{'}}u20<x\le 100\\ 8000n{ê}^{\text{'}}u100<x\le 250\end{array}\right.$

b) Nếu bạn Dương gửi thư có khối lượng x = 150 g mà 100 < 150 < 250 nên tiền cước phải trả là y = 8 000 đồng.

Nếu bạn Dương gửi thư có khối lượng x = 200 g mà 100 < 200 < 250 nên tiền cước phải trả là y = 8 000 đồng.

Số tiền phải trả khi bạn Dương gửi thư có khối lượng 150 g, 200 g là:

8 000 + 8 000 = 16 000 (đồng).

Vậy tổng số tiền bạn Dương phải trả khi gửi thư có khối lượng 150g và 200g là 16 000 đống.

Bài 4 trang 38 Toán lớp 10 Tập 1: Cho hàm số y = – 2x².

a) Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng – 2; 3 và 10.

b) Tìm những điểm thuộc đồ thị hàm số có tung độ bằng – 18. 

Lời giải:

a) Điểm có hoành độ bằng – 2 hay x = – 2 thì tung độ y = (– 2) . (– 2)2 = – 8.

Điểm có hoành độ bằng 3 hay x = 3 thì tung độ y = (– 2) . 32 = – 18.

Điểm có hoành độ bằng 10 hay x = 10 thì tung độ y = (– 2) . 102 = – 200. 

Vậy các điểm cần tìm có tọa độ là (– 2; – 8), (3; – 18) và (10; – 200). 

b) Điểm có tung độ bằng – 18 hay y = – 18.

Khi đó: – 2x2 = – 18 ⇔ x2 = 9 ⇔ x = ± 3. 

Vậy các điểm thuộc đồ thị hàm số có tung độ bằng – 18 là (3; – 18) và (– 3; – 18).

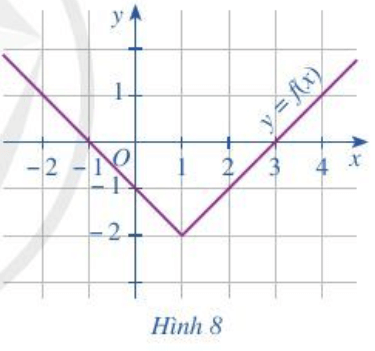
Bài 5 trang 38 Toán lớp 10 Tập 1: Cho đồ thị hàm số y = f(x) như Hình 8.

a) Trong các điểm có tọa độ (1; – 2), (0; 0), (2; – 1), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số? 

b) Xác định f(0); f(3).

c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 0. 

Lời giải:

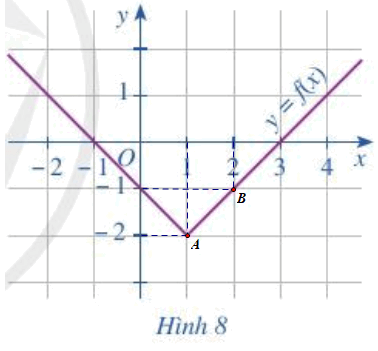
 a) Xác định các điểm A(1; – 2), O(0; 0) và B(2; – 1) lên mặt phẳng tọa độ ở Hình 8:

Dựa vào hình vẽ ta thấy:

Đồ thị hàm số y = f(x) không đi qua điểm O(0; 0) nên điểm O(0; 0) không thuộc đồ thị hàm số đã cho.

Đồ thị hàm số đi qua hai điểm A, B nên hai điểm A(1; – 2) và B(2; – 1) thuộc đồ thị hàm số đã cho.

Vậy điểm có tọa độ (1; -2) và (2; -1) thuộc đồ thị hàm số và điểm có tọa độ (0; 0) không thuộc đồ thị hàm số đã cho.

b) Tại x = 0 dóng đường thẳng vuông góc với trục Ox cắt đồ thị hàm số tại điểm có tọa độ (0; -1) nên f(0) = -1.

Tại x = 3 dóng đường thẳng vuông góc với trục Ox cắt đồ thị hàm số tại điểm có tọa độ (3; 0) nên f(3) = 0.

Vậy f(0) = – 1; f(3) = 0.

c) Điểm thuộc đồ thị có tung độ bằng 0 hay y = 0

Tại điểm có y = 0 dóng đường thẳng vuông góc với trục tung cắt đồ thị tại điểm có tọa độ (3; 0).

Vậy điểm thuộc đồ thị có tung độ bằng 0 là điểm có tọa độ (3; 0).

Bài 6 trang 38 Toán lớp 10 Tập 1: Cho hàm số $y=\frac{1}{x}$. Chứng tỏ hàm số đã cho: 

a) Nghịch biến trên khoảng (0; + ∞);

b) Nghịch biến trên khoảng (– ∞; 0).

Lời giải:

Ta có: $y=f\left(x\right)=\frac{1}{x}$.

Biểu thức $\frac{1}{x}$ xác định khi x ≠ 0.

Do đó tập xác định của hàm số đã cho: D = $ℝ\backslash \left\{0\right\}$.

a) Lấy hai giá trị x₁, x₂ tùy ý thuộc khoảng (0; + ∞) sao cho 0 < x₁ < x₂.

Khi đó $f\left(x_1\right)=\frac{1}{x_1}$ và $f\left(x_2\right)=\frac{1}{x_2}$

Vì  0 < x₁ < x₂  nên $\frac{1}{x_1}>\frac{1}{x_2}$ hay f(x₁) > f(x₂).

Vậy hàm số đã cho nghịch biến trên khoảng (0; + ∞).

b) Lấy hai giá trị x₁, x₂ tùy ý thuộc khoảng (– ∞; 0) sao cho x₁ < x₂ < 0.

Khi đó $f\left(x_1\right)=\frac{1}{x_1}$ và $f\left(x_2\right)=\frac{1}{x_2}$

Vì x₁ < x₂ < 0 nên $\frac{1}{x_1}>\frac{1}{x_2}$ hay f(x₁) > f(x₂).

Vậy hàm số đã cho nghịch biến trên khoảng (– ∞; 0).

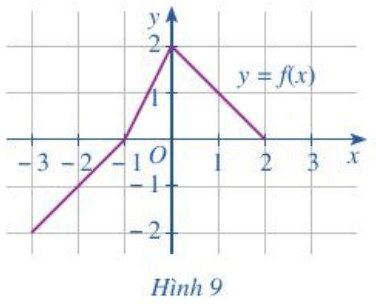
Bài 7 trang 38 Toán lớp 10 Tập 1: Cho hàm số y = f(x) có đồ thị như Hình 9.

Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

Lời giải:

Quan sát đồ thị hàm số y = f(x) ở Hình 9, ta thấy:

+) Trong khoảng (-3; 0) đồ thị hàm số đã cho “đi lên” nên hàm số đã cho đồng biến trên khoảng (-3; 0)

+) Trong khoảng (0; 2) đồ thị hàm số đã cho “đi xuống” nên hàm số đã cho nghịch biến trên khoảng (0; 2).

Vậy hàm số đã cho đồng biến trên khoảng (-3; 0) và nghịch biến trên khoảng (0; 2).

Bài 8 trang 38 Toán lớp 10 Tập 1: Một lớp muốn thuê một chiếc xe khách cho chuyến tham quan với tổng đoạn đường cần di chuyển trong khoảng từ 550 km đến 600 km, có hai công ty được tiếp cận để tham khảo giá.

Công ty A có giá khởi đầu là 3,75 triệu đồng cộng thêm 5 000 đồng cho mỗi ki-lô-mét chạy xe. 

Công ty B có giá khởi đầu là 2,5 triệu đồng cộng thêm 7 500 đồng cho mỗi ki-lô-mét chạy xe. Lớp đó nên chọn công ty nào để chi phí là thấp nhất? 

Lời giải:

Đổi 3,75 triệu đồng = 3 750 000 đồng; 2,5 triệu đồng = 2 500 000 đồng.

Gọi x (km) là tổng đoạn đường cần di chuyển của lớp (550 ≤ x ≤ 600) và y là chi phí lớp đó phải trả cho việc thuê xe.

Ta có với mỗi giá trị của x có đúng một giá trị của y nên y là hàm số của x.

Đối với công ty A, ta có số tiền cần trả được biểu diễn theo hàm số: 

y_A = 3 750 000 + 5000x

Vì 550 ≤ x ≤ 600 nên 6 500 000 ≤ 3 750 000 + 5000x ≤ 6 750 000 hay 6 500 000 ≤  y_A ≤ 6 750 000.

Đối với công ty B, ta có số tiền cần trả được biểu diễn theo hàm số: 

y_B = 2 500 000 + 7500x

Vì 550 ≤ x ≤ 600 nên 6 625 000 ≤ 2 500 000 + 7500x  ≤ 7 000 000 hay 6 625 000 ≤ y_B ≤ 7 000 000.

Ta thấy khoảng chi phí cho việc thuê xe của công ty A thấp hơn so với khoảng chi phí cho việc thuê xe ở công ty B với cùng số ki – lô – mét di chuyển.

Vậy để chi phí là thấp nhất thì lớp đó nên chọn xe của công ty A.