Giải bài tập Toán 10 Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

A. Các câu hỏi trong bài

Khởi động trang 35 Toán 10 Tập 2: Kết quả 5 bài kiểm tra môn Toán của hai bạn Dũng và Huy được thống kê trong bảng sau:

Bảng 4

Kết quả làm bài kiểm tra môn Toán của bạn nào đồng đều hơn?

Lời giải

Số trung bình cộng điểm kiểm tra của bạn Dũng là:

$\overline{x_D}=\frac{8+6+7+5+9}{5}=7$.

Số trung bình cộng điểm kiểm tra của bạn Huy là:

$\overline{x_H}=\frac{6+7+7+8+7}{5}=7$.

Ta thấy điểm trung bình bài kiểm tra môn Toán của hai bạn Dũng và Huy là như nhau, vậy ta không thể dùng số liệu này để trả lời yêu cầu của bài toán.

Sau bài học này ta sẽ tính được như sau:

Phương sai mẫu số liệu điểm kiểm tra của bạn Dũng là:

$s_D^2=\frac{{\left(8-7\right)}^2+{\left(6-7\right)}^2+{\left(7-7\right)}^2+{\left(5-7\right)}^2+{\left(9-7\right)}^2}{5}=2$.

Phương sai mẫu số liệu điểm kiểm tra của bạn Huy là:

$s_H^2=\frac{{\left(6-7\right)}^2+{\left(7-7\right)}^2+{\left(7-7\right)}^2+{\left(8-7\right)}^2+{\left(7-7\right)}^2}{5}=\frac{2}{5}=\mathrm{0,4}$.

Vì 0,4 < 2 nên $s_H^2<s_D^2$, nghĩa là mức độ phân tán điểm bài kiểm tra của bạn Huy ít hơn so với bạn Dũng.

Vậy bạn Huy có kết quả kiểm tra môn Toán đồng đều hơn bạn Dũng.

Hoạt động 1 trang 35 Toán 10 Tập 2: Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau:

2 5 16 8 7 9 10 12 14 11 6 (1)

a) Tìm hiệu giữa số đo lớn nhất và số đo nhỏ nhất.

b) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần. Tìm các giá trị Q₁, Q₂, Q₃ là tứ phân vị của mẫu đó. Sau đó, tìm hiệu Q₃ – Q₁.

Lời giải

a) Số đo lớn nhất là x_max = 16, số đo nhỏ nhất là x_min = 2.

Hiệu giữa số đo lớn nhất và số đo nhỏ nhất là R = x_max– x_min = 16 – 2 = 14.

b) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần ta được:

2 5 6 7 8 9 10 11 12 14 16

Dãy trên có 11 số liệu nên trung vị là số thứ sáu.

Trung vị của mẫu (1) là Q₂ = 9.

Trung vị của dãy 2, 5, 6, 7, 8 là Q₁ = 6.

Trung vị của dãy 10, 11, 12, 14, 16 là Q₃ = 12.

Vậy Q₁ = 6, Q₂ = 9, Q₃ = 12.

Vậy hiệu Q₃ – Q₁ = 12 – 6 = 6.

Hoạt động 2 trang 37 Toán 10 Tập 2: Số liệu thống kê kết quả 5 bài kiểm tra môn Toán của bạn Dũng là: 8    6 7     5      9 (3) (xem Bảng 4).

Số trung bình cộng của mẫu số liệu (3) là:

$\overline{x}=\frac{8+6+7+5+9}{5}=7$.

a) Tính các độ lệch sau: (8 – 7); (6 – 7); (7 – 7); (5 – 7); (9 – 7).

b) Tính bình phương các độ lệch và tính trung bình cộng của chúng.

Lời giải

a) Ta tính được các độ lệch là:

(8 – 7) = 1; (6 – 7) = – 1; (7 – 7) = 0; (5 – 7) = – 2; (9 – 7) = 2.

b) Bình phương các độ lệch là:

(8 – 7)² = 1² = 1; (6 – 7)² = (– 1)² = 1; (7 – 7)² = 0² = 0;

(5 – 7) = (– 2)² = 4; (9 – 7)² = 2² = 4.

Trung bình cộng của bình phương các độ lệch là:

$\frac{{\left(8-7\right)}^2+{\left(6-7\right)}^2+{\left(7-7\right)}^2+{\left(5-7\right)}^2+{\left(9-7\right)}^2}{5}=$$\frac{1+1+0+4+4}{5}=2$.

Luyện tập 1 trang 38 Toán 10 Tập 2: Mẫu số liệu về thời gian (đơn vị: giây) chạy cự li 500 m của 5 người là: 

55,2 58,8 62,4 54 59,4 (5)

Mẫu số liệu về thời gian (đơn vị: giây) chạy cự li 1 500 m của 5 người đó là:

271,2   261  276 282  270  (6)

Tính phương sai của mẫu (5) và mẫu (6). Từ đó cho biết cự li chạy nào có kết quả đồng đều hơn.

Lời giải:

Số trung bình cộng của mẫu số liệu (5) là:

$\overline{x_{\left(5\right)}}=\frac{\mathrm{55,2}+\mathrm{58,8}+\mathrm{62,4}+54+\mathrm{59,4}}{5}=\mathrm{57,96}$.

Phương sai của mẫu số liệu (5) là:

$s_{\left(5\right)}^2=\frac{{\left(\mathrm{55,2}-\mathrm{57,96}\right)}^2+{\left(\mathrm{58,8}-\mathrm{57,96}\right)}^2+{\left(\mathrm{62,4}-\mathrm{57,96}\right)}^2+{\left(54-\mathrm{57,96}\right)}^2+{\left(\mathrm{59,4}-\mathrm{57,96}\right)}^2}{5}$

= 9,1584.

Số trung bình cộng của mẫu số liệu (6) là:

$\overline{x_{\left(6\right)}}=\frac{\mathrm{271,2} +261 +276 +282 +270}{5}=\mathrm{272,04}$.

Phương sai của mẫu số liệu (6) là:

$s_{\left(6\right)}^2=\frac{1}{5}$[(271,2 − 272,04)² + (261 − 272,04)² + (276 − 272,04)² + (282 − 272,04)² + (270 − 272,04)²] = 48,3264.

Vì 9,1584 < 48,3264 nên $s_{\left(5\right)}^2<s_{\left(6\right)}^2$.

Vậy cự li chạy 500 m có kết quả đồng đều hơn.

Hoạt động 3 trang 39 Toán 10 Tập 2: Trong Ví dụ 2, phương sai của mẫu số liệu (4) là $s_H^2=\mathrm{0,4}$. Tính $s_H=\sqrt{s_H^2}$.

Lời giải

Ta có: $s_H=\sqrt{s_H^2}=\sqrt{\mathrm{0,4}}=\frac{\sqrt{10}}{5}\approx \mathrm{0,63}$.

Luyện tập 2 trang 39 Toán 10 Tập 2: Mẫu số liệu về số lượng áo bán ra lần lượt từ tháng 1 đến tháng 12 của một doanh nghiệp là: 

430 560 450  550  760  430 525 410  635  450  800  900

Tính độ lệch chuẩn của mẫu số liệu đó.

Lời giải:

Số trung bình cộng của mẫu số liệu đã cho là:

$\overline{x}=\frac{430+560+450+550+760+430+525+410+635+450+800+900}{12}=575$.

Phương sai của mẫu số liệu trên là:

$s^2=\frac{1}{12}$[(430 − 575)² + (560 − 575)² + (450 − 575)² + (550 − 575)² + (760 – 575)² + (430 − 575)² + (525 – 575)² + (410 − 575)² + (635 − 575)² + (450 − 575)² + (800 − 575)² + (900 – 575)²] ≈ 24829,17.

Vậy độ lệch chuẩn của mẫu số liệu trên là: s = $\sqrt{s^2}=\sqrt{\mathrm{24829,17}}\approx \mathrm{157,57}$.

B. Bài tập

Bài 1 trang 41 Toán 10 Tập 2: Trong 5 lần nhảy xa, hai bạn Hùng và Trung có kết quả (đơn vị: mét) lần lượt là

a) Kết quả trung bình của hai bạn có bằng nhau hay không?

b) Tính phương sai của mẫu số liệu thống kê kết quả 5 lần nhảy xa của mỗi bạn. Từ đó cho biết bạn nào có kết quả nhảy xa ổn định hơn. 

Lời giải

a) Kết quả trung bình của Hùng là:

$\overline{x_H}=\frac{\mathrm{2,4}+\mathrm{2,6}+\mathrm{2,4}+\mathrm{2,5}+\mathrm{2,6}}{5}=\mathrm{2,5}$.

Kết quả trung bình của Trung là:

$\overline{x_T}=\frac{\mathrm{2,4}+\mathrm{2,5}+\mathrm{2,5}+\mathrm{2,5}+\mathrm{2,6}}{5}=\mathrm{2,5}$.

Vậy kết quả trung bình của hai bạn có bằng nhau.

b) Phương sai của mẫu số liệu kết quả nhảy xa của bạn Hùng là:

$s_H^2=\frac{{\left(\mathrm{2,4}-\mathrm{2,5}\right)}^2+{\left(\mathrm{2,6}-\mathrm{2,5}\right)}^2+{\left(\mathrm{2,4}-\mathrm{2,5}\right)}^2+{\left(\mathrm{2,5}-\mathrm{2,5}\right)}^2+{\left(\mathrm{2,6}-\mathrm{2,5}\right)}^2}{5}=\mathrm{0,008}$.

 Phương sai của mẫu số liệu kết quả nhảy xa của bạn Trung là:

$s_T^2=\frac{{\left(\mathrm{2,4}-\mathrm{2,5}\right)}^2+{\left(\mathrm{2,5}-\mathrm{2,5}\right)}^2+{\left(\mathrm{2,5}-\mathrm{2,5}\right)}^2+{\left(\mathrm{2,5}-\mathrm{2,5}\right)}^2+{\left(\mathrm{2,6}-\mathrm{2,5}\right)}^2}{5}=\mathrm{0,004}$.

Vì 0,04 < 0,08 nên $s_T^2<s_H^2$.

Vậy bạn Trung có kết quả nhảy xa ổn định hơn.

Bài 2 trang 41 Toán 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 3 biểu diễn tốc độ tăng trưởng GDP của Việt Nam giai đoạn 2012 – 2019. 

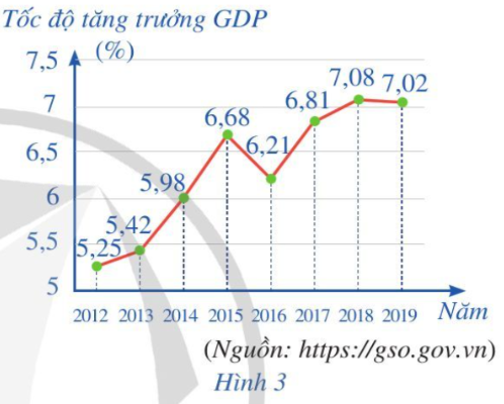
a) Viết mẫu số liệu thống kê tốc độ tăng trưởng GDP nhận được từ biểu đồ ở Hình 3. 

b) Tìm khoảng biến thiên của mẫu số liệu đó. 

c) Tìm khoảng tứ phân vị của mẫu số liệu đó. 

d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải

a) Từ biểu đồ ở Hình 3, mẫu số liệu thống kê tốc độ tăng trưởng GDP là:

5,25   5,42   5,98   6,68   6,21   6,81   7,08   7,02

b) Ta sắp xếp mẫu số liệu theo thứ tự không giảm như sau:

5,25   5,42   5,98   6,21   6,68   6,81   7,02   7,08

Khoảng biến thiên của mẫu số liệu là:

R = 7,08 – 5,25 = 1,83.

c) Mẫu gồm 8 số liệu. Do đó ta có:

Trung vị của mẫu số liệu là: Q₂ = $\frac{\mathrm{6,21}+\mathrm{6,68}}{2}=\mathrm{6,445}$.

Trung vị của dãy 5,25; 5,42; 5,98; 6,21 là: Q₁ = $\frac{\mathrm{5,42}+\mathrm{5,98}}{2}=\mathrm{5,7}$.

Trung vị của dãy 6,68; 6,81; 7,02; 7,08 là: Q₃ = $\frac{\mathrm{6,81}+\mathrm{7,02}}{2}=\mathrm{6,915}$.

Vậy khoảng tứ phân vị của mẫu số liệu đó là:

∆_Q = Q₃ – Q₁ = 6,915 – 5,7 = 1,215.

d) Số trung bình của mẫu số liệu là:

$\overline{x}=\frac{\mathrm{5,25} +\mathrm{5,42} +\mathrm{5,98} +\mathrm{6,21} +\mathrm{6,68} +\mathrm{6,81} +\mathrm{7,02} +\mathrm{7,08}}{8}=\mathrm{6,30625}$.

Phương sai của mẫu số liệu là:

$s^2=\frac{1}{8}$[(5,25 − 6,30625)² + (5,42 − 6,30625)² + (5,98 − 6,30625)² + (6,21 − 6,30625)² + (6,68 − 6,30625)² + (6,81 − 6,30625)² + (7,02 – 6,30625)² + (7,08 – 6,30625)²] ≈ 0,4398.

Độ lệch chuẩn của mẫu số liệu là: s = $\sqrt{s^2}\approx \sqrt{\mathrm{0,4398}}\approx \mathrm{0,6632}$.

Bài 3 trang 41 Toán 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021. 

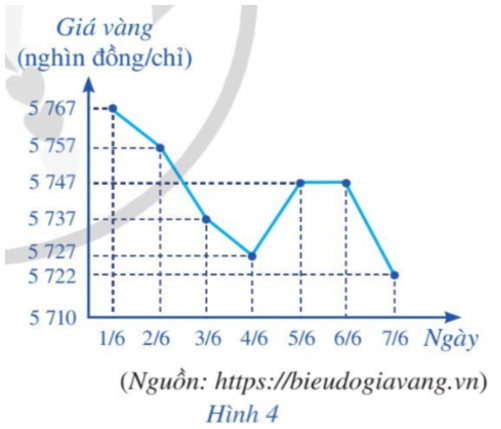
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.

b) Tìm khoảng biến thiên của mẫu số liệu đó. 

c) Tìm khoảng tứ phân vị của mẫu số liệu đó. 

d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải

a) Mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4 là:

5 767     5 757     5 737     5 727     5 747      5 747     5 722

b) Ta sắp xếp mẫu số liệu theo thứ tự không giảm như sau:

5 722      5 727     5 737     5 747     5 747     5 757     5 767

Vậy khoảng biến thiên của mẫu số liệu là:

R = 5 767 – 5 722 = 45.

c) Mẫu số liệu gồm 7 số. Do đó ta có:

Trung vị của mẫu số liệu là: Q₂ = 5 747.

Trung vị của dãy 5 722; 5 727; 5 737  là: Q₁ = 5 727.

Trung vị của dãy 5 747; 5 757; 5 767 là: Q₃ = 5 757.

Vậy khoảng tứ phân vị của mẫu số liệu là:

∆_Q = Q₃ – Q₁ = 5 757 – 5 727 = 30.

d) Số trung bình cộng của mẫu số liệu là:

$\overline{x}=\frac{5722 +5727 +5737 +5747 +5747 +5757 +5767}{7}\approx \mathrm{5743,43}$.

Phương sai của mẫu số liệu là:

$s^2=\frac{1}{7}$[(5 722 – 5 743,43)² + (5 727 – 5 743,43)² + (5 737 – 5 743,43)² + (5 747 – 5 743,43)² + (5 747 – 5 743,43)² + (5 757 – 5 743,43)² + (5 767 – 5 743,43)²] ≈ 219,39.

Độ lệch chuẩn của mẫu số liệu là: $s=\sqrt{s^2}\approx \sqrt{\mathrm{219,39}}\approx \mathrm{14,81}$.

Bài 4 trang 41 Toán 10 Tập 2: Để biết cây đậu phát triển như thế nào sau khi gieo hạt, bạn Châu gieo 5 hạt  đậu vào 5 chậu riêng biệt và cung cấp cho chúng lượng nước, ánh sáng như nhau. Sau hai tuần, 5 hạt đậu đã nảy mầm và phát triển thành 5 cây con. Bạn Châu đo chiều cao từ rễ đến ngọn của mỗi cây (đơn vị: mi-li-mét) và ghi kết quả là mẫu số liệu sau:

112 102  106  94  101

a) Tính phương sai và độ lệch chuẩn của mẫu số liệu trên. 

b) Theo em, các cây có phát triển đồng đều hay không?

Lời giải

a) Số trung bình cộng của mẫu số liệu đã cho là:

$\overline{x}=\frac{112+102+106+94+101}{5}=103$.

Phương sai của mẫu số liệu trên là:

$s^2=\frac{{\left(112-103\right)}^2+{\left(102-103\right)}^2+{\left(106-103\right)}^2+{\left(94-103\right)}^2+{\left(101-103\right)}^2}{5}=\mathrm{35,2}$.

Độ lệch chuẩn của mẫu số liệu là:

s = $\sqrt{s^2}=\sqrt{\mathrm{35,2}}=\frac{4\sqrt{55}}{5}\approx \mathrm{5,93}$.

b) Vì độ lệch chuẩn của mẫu số liệu là khoảng 5,93, số này khá cao, do đó theo em các cây phát triển không đồng đều.