Giải bài tập Toán 10: Bài tập cuối chương 6 

Bài 1 trang 53 Toán 10 Tập 2: Cho mẫu số liệu:  1    2    4    5   9   10    11.

a) Số trung bình cộng của mẫu số liệu trên là:

A. 5.

B. 5,5. 

C. 6.

D. 6,5. 

b) Trung vị của mẫu số liệu trên là:

A. 5. 

B. 5,5. 

C. 6.

D. 6,5. 

c) Tứ phân vị của mẫu số liệu trên là:

A. Q₁ = 4, Q₂ = 5, Q₃ = 9.

B. Q₁ = 1, Q₂ = 5,5, Q₃ = 11.

C. Q₁ = 1, Q₂ = 5, Q₃ = 11.

D. Q₁ = 2, Q₂ = 5, Q₃ = 10.

d) Khoảng biến thiên của mẫu số liệu trên là:

A. 5.

B. 6.

C. 10. 

D. 11. 

e) Khoảng tứ phân vị của mẫu số liệu trên là:

A. 7.

B. 8. 

C. 9.

D. 10.

g) Phương sai của mẫu số liệu trên là:

A. $\sqrt{\frac{96}{7}}$.

B. $\frac{96}{7}$.

C. 96.

D. $\sqrt{96}$.

h) Độ lệch chuẩn của mẫu số liệu trên là:

A. $\sqrt{\frac{96}{7}}$.

B. $\frac{96}{7}$.

C. 96.

D. $\sqrt{96}$.

Lời giải

a) Đáp án đúng là: C.

Số trung bình cộng của mẫu số liệu đã cho là: $\overline{x}=\frac{1+2+4+5+9+10+11}{7}=6$.

b) Đáp án đúng là: A.

Mẫu số liệu cho ở trên đã được sắp xếp theo thứ tự không giảm.

Vì mẫu gồm 7 số liệu nên trung vị mẫu là số thứ tư, do đó M_e = 5.

c) Đáp án đúng là: D.

Tứ phân vị thứ hai là Q₂ = M_e = 5.

Tứ phân vị thứ nhất là trung vị của dãy 1; 2; 4 nên Q₁ = 2.

Tứ phân vị thứ ba là trung vị của dãy 9; 10; 11 nên Q₃ = 10.

Vậy Q₁ = 2, Q₂ = 5, Q₃ = 10.

d) Đáp án đúng là: C.

Khoảng biến thiên của mẫu số liệu là: R = 11 – 1 = 10.

e) Đáp án đúng là: B.

Khoảng tứ phân vị của mẫu số liệu là ∆_Q = Q₃ – Q₁ = 10 – 2 = 8.

g) Đáp án đúng là: B.

Phương sai của mẫu số liệu trên là:

 s² = $\frac{1}{7}$[(1 – 6)² + (2 – 6)² + (4 – 6)² + (5 – 6)² + (9 – 6)² + (10 – 6)² + (11 – 6)²] = $\frac{96}{7}$.

h) Đáp án đúng là: A.

Độ lệch chuẩn của mẫu số liệu trên là s = $\sqrt{s^2}=\sqrt{\frac{96}{7}}$.

Bài 2 trang 53 Toán 10 Tập 2: Bảng 6 thống kê số áo sơ mi nam bán được của một cửa hàng trong một tháng.

Bảng 6

Mốt của mẫu số liệu trên là bao nhiêu?

A. 42.

B. 47.

C. 32.

D. 39.

Lời giải

Đáp án đúng là: D.

Từ bảng tần số ta thấy cỡ áo 39 có tần số lớn nhất nên mốt của mẫu số liệu là M₀ = 39.

Bài 3 trang 53, 54 Toán 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 6 cho biết lượng khách du lịch quốc tế đến Việt Nam trong một số năm (từ 1990 đến 2019).

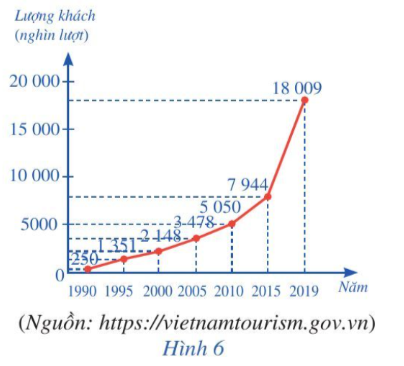
a) Viết mẫu số liệu thống kê số lượt khách du lịch quốc tế đến Việt Nam nhận được từ biểu đồ bên.

b) Viết mẫu số liệu theo thứ tự tăng dần. Tìm số trung bình cộng, trung vị và tứ phân vị của mẫu số liệu đó.

c) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.

d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải

a) Mẫu số liệu thống kê số lượt khách du lịch quốc tế đến Việt Nam nhận được từ biểu đồ đã cho là:     250      1 351      2 148      3 478      5 050      7 944      18 009.

b) Sắp xếp mẫu số liệu trên theo thứ tự tăng dần ta được:

250      1 351      2 148      3 478      5 050      7 944      18 009

Số trung  bình cộng của mẫu số liệu trên là:

$\overline{x}=\frac{250+1351+2148+3478+5050+7944+18009}{7}\approx \mathrm{5461,43}$.

Mẫu số liệu trên có 7 số liệu nên trung vị là số thứ 4, do đó M_e = 3 478.

Tứ phân vị thứ hai của mẫu số liệu trung vị của mẫu nên Q₂ = 3 478.

Trung vị của dãy 250; 1 351; 2 148 là Q₁ = 1 351.

Trung vị của dãy 5 050; 7 944; 18 009 là Q₃ = 7 944.

Vậy các tứ phân vị của mẫu số liệu trên là: Q₁ = 1 351, Q₂ = 3 478, Q₃ = 7 944.

c) Khoảng biến thiên của mẫu số liệu trên là: R = 18 009 – 250 = 17 759.

Khoảng tứ phân vị của mẫu số liệu trên là: Δ_Q = Q₃ – Q₁ = 7 944 – 1 351 = 6 593.

d) Phương sai của mẫu số liệu trên là:

$s^2=\frac{1}{7}$.[(250 – 5 461,43)² + (1 351 – 5 461,43)² + (2 148 – 5 461,43)² + (3 478 – 5 461,43)² + (5 050 – 5 461,43)² + (7 944 – 5 461,43)² + (18 009 – 5 461,43)²]

= 31820198,82.

Độ lệch chuẩn của mẫu số liệu trên là: $s=\sqrt{s^2}=\sqrt{\mathrm{31820198,82}}\approx \mathrm{5640,94}$.

Bài 4 trang 54 Toán 10 Tập 2: Lớp 10A có 40 học sinh. Tỉ số phần trăm về phương tiện mà các bạn đến trường được mô tả như biểu đồ ở Hình 7.

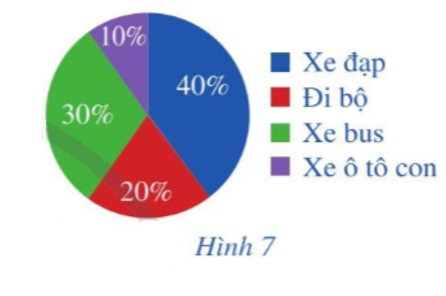
a) Có bao nhiêu bạn đi xe đạp đến trường?

b) Chọn ngẫu nhiên một bạn để phân công vào đội xung kích của trường. Tính xác suất của biến cố “Bạn được chọn là bạn đến trường bằng xe đạp”.

Lời giải

a) Từ biểu đồ Hình 7 ta thấy số bạn đi xe đạp đến trường chiếm 40% tổng số bạn học sinh của lớp 10A.

Vì lớp 10A có 40 học sinh nên số bạn đi xe đạp đến trường là:

40 . 40% = 40 . 40 : 100 = 16 (bạn).

Vậy có 16 bạn đi xe đạp đến trường.

b) Chọn 1 bạn trong 40 bạn của lớp để phân công vào đội xung kích, có 40 cách chọn, do đó n(Ω) = 40.

Gọi biến cố D: “Bạn được chọn là bạn đến trường bằng xe đạp”.

Vì  có 16 bạn đi xe đạp đến trường, chọn 1 bạn trong 16 bạn này thì có 16 cách chọn hay n(D) = 16.

Vậy xác suất của biến cố D là $P\left(D\right)=\frac{n\left(D\right)}{n\left(\Omega \right)}=\frac{16}{40}=\frac{2}{5}$.

Bài 5 trang 54 Toán 10 Tập 2: Em hãy tìm hiểu chiều cao của tất cả các bạn trong tổ và lập mẫu số liệu với kết quả tăng dần. Với mẫu số liệu đó, hãy tìm:

a) Số trung bình cộng, trung vị và tứ phân vị;

b) Khoảng biến thiên và khoảng tứ phân vị;

c) Phương sai và độ lệch chuẩn.

Lời giải

Giả sử, tổ II của lớp 10A1 có 6 bạn học sinh. Đo chiều cao (đơn vị: cm) của 6 bạn này được mẫu số liệu sắp xếp theo thứ tự tăng dần như sau:

152 157 160 165 168 172.

a) Số trung bình cộng của mẫu trên là:

$\overline{x}=\frac{152+157+160+165+168+172}{6}\approx \mathrm{162,33}$.

Mẫu số liệu gồm 6 số liệu. Số thứ ba là 160, số thứ tư là 165.

Khi đó, trung vị của mẫu là M_e = $\frac{160+165}{2}=\mathrm{162,5}$.

Tứ phân vị thứ hai là Q₂ = M_e = 162,5.

Trung vị của dãy 152; 157; 160 là Q₁ = 157.

Trung vị của dãy 165; 168; 172 là Q₃ = 168.

Vậy các tứ phân vị của mẫu là Q₁ = 157, Q₂ = 162,5, Q₃ = 168.

b) Khoảng biến thiên của mẫu là R = 172 – 152 = 20.

Khoảng tứ phân vị của mẫu là ∆_Q = Q₃ – Q₁ = 168 – 157 = 11.

c) Phương sai của mẫu là:

$s^2=\frac{1}{6}$[(152 – 162,33)² + (157 – 162,33)² + (160 – 162,33)² + (165 – 162,33)² + (168 – 162,33)² + (172 – 162,33)² ≈ 45,56.

Độ lệch chuẩn của mẫu là $s=\sqrt{s^2}\approx \sqrt{\mathrm{45,56}}\approx \mathrm{6,75}$.

Bài 6 trang 54 Toán 10 Tập 2: Trong một hội thảo quốc tế có 10 chuyên gia đến từ các nước ở châu Á, 12 chuyên gia đến từ các nước ở châu Âu. Chọn ngẫu nhiên 2 chuyên gia vào ban tổ chức. Xác suất của biến cố “Chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức” bằng bao nhiêu?

Lời giải

Tổng số chuyên gia trong hội thảo đến từ các nước ở châu Á và châu Âu là:

10 + 12 = 22 (chuyên gia).

Mỗi cách chọn ngẫu nhiên 2 chuyên gia vào ban tổ chức là một tổ hợp chập 2 của 22 phần tử. Vậy không gian mẫu Ω là số các tổ hợp chập 2 của 22 phần tử.

Nên n(Ω) = $C_{22}^2=231$.

Gọi biến cố C: “Chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức”.

Để chọn được 2 chuyên gia ở 2 châu lục khác nhau, ta chọn 1 chuyên gia đến từ các nước ở châu Á và 1 chuyên gia đến từ các nước ở châu Âu. Ta có:

- Chọn 1 chuyên gia đến từ các nước ở châu Á trong 10 chuyên gia, có 10 cách chọn.

- Chọn 1 chuyên gia đến từ các nước ở châu Âu trong 12 chuyên gia, có 12 cách chọn.

Theo quy tắc nhân, vậy có 10 . 12 = 120 cách chọn 2 chuyên gia ở hai châu lục khác nhau. Do đó n(C) = 120.

Vậy xác suất của biến cố C là $P\left(C\right)=\frac{n\left(C\right)}{n\left(\Omega \right)}=\frac{120}{231}=\frac{40}{77}$.

Bài 7 trang 54 Toán 10 Tập 2: Trong một buổi khiêu vũ có đúng 10 cặp vợ chồng. Chọn ngẫu nhiên 2 người lên khiêu vũ đầu tiên. Xác suất của biến cố “Chọn được 2 người là vợ chồng” bằng bao nhiêu?

Lời giải

Ta có: 10 cặp vợ chồng là 20 người.

Mỗi cách chọn ngẫu nhiên 2 người lên khiêu vũ trong 20 người trên là một tổ hợp chập 2 của 20 phần tử nên không gian mẫu Ω là số các tổ hợp chập 2 của 20 phần tử.

Vậy n(Ω) = $C_{20}^2=190$.

Gọi biến cố V: “Chọn được 2 người là vợ chồng”.

Do có đúng 10 cặp vợ chọn nên chọn 2 người là vợ chồng thì có 10 cách chọn hay n(V) = 10.

Vậy xác suất của biến cố V là $P\left(V\right)=\frac{n\left(V\right)}{n\left(\Omega \right)}=\frac{10}{190}=\frac{1}{19}$.

Bài 8 trang 54 Toán 10 Tập 2: Một lô hàng có 20 sản phẩm bao gồm 16 chính phẩm và 4 phế phẩm. Chọn ngẫu nhiên 3 sản phẩm.

a) Có bao nhiêu kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm?

b) Xác suất của biến cố “Cả 3 sản phẩm được chọn là chính phẩm” bằng bao nhiêu?

Lời giải

a) Mỗi cách chọn ngẫu nhiên 3 sản phẩm trong 20 sản phẩm là một tổ hợp chập 3 của 20 phần tử nên số cách chọn ngẫu nhiên 3 sản phẩm là số các tổ hợp chập 3 của 20 phần tử và là $C_{20}^3=1140$.

Vậy có 1 140 kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm.

b) Theo câu a ta có số phần tử của không gian mẫu là n(Ω) = 1 140.

Gọi biến cố H: “Cả 3 sản phẩm được chọn là chính phẩm”.

Trong 20 sản phẩm thì có 16 chính phẩm nên chọn 3 sản phẩm là chính phẩm trong 16 chính phẩm có số cách chọn là $C_{16}^3=560$ hay n(H) = 560.

Vậy xác suất của biến cố H là $P\left(H\right)=\frac{n\left(H\right)}{n\left(\Omega \right)}=\frac{560}{1140}=\frac{28}{57}$.

Bài 9 trang 54 Toán 10 Tập 2: Trong một hộp có 20 chiếc thẻ cùng loại được viết các số 1, 2, 3, ..., 20 sao cho mỗi thẻ chỉ viết một số và hai thẻ khác nhau viết hai số khác nhau. Chọn ngẫu nhiên 2 chiếc thẻ. Tính xác suất của biến cố “Hai thẻ được chọn có tích của hai số được viết trên đó là số lẻ”.

Lời giải

Mỗi cách chọn ngẫu nhiên 2 chiếc thẻ trong một hộp gồm 20 chiếc thẻ là một tổ hợp chập 2 của 20 phần tử nên không gian mẫu Ω là số các tổ hợp chập 2 của 20 phần tử.

Vậy n(Ω) = $C_{20}^2=190$.

Gọi biến cố L: “Hai thẻ được chọn có tích của hai số được viết trên đó là số lẻ”.

Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đó đều là số lẻ.

Ta có các số tự nhiên lẻ từ 1 đến 20 là: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19. Có 10 số lẻ từ 1 đến 20 nên có 10 chiếc thẻ ghi số lẻ.

Chọn 2 thẻ ghi số lẻ trong 10 thẻ ghi số lẻ thì số cách chọn là $C_{10}^2=45$.

Do đó n(L) = 45.

Vậy xác suất của biến cố L là $P\left(L\right)=\frac{n\left(L\right)}{n\left(\Omega \right)}=\frac{45}{190}=\frac{9}{38}$.