Giải bài tập Toán 10 Bài 2: Giải tam giác

Khởi động trang 72 Toán lớp 10 Tập 1: Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để do khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,…) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:

Từ vị trí A, đo góc nghiêng α so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng β so với bờ biển tới vị trí C đã chọn (Hình 18). Bằng cách giải tam giác BAC, họ tính được khoảng cách AC.

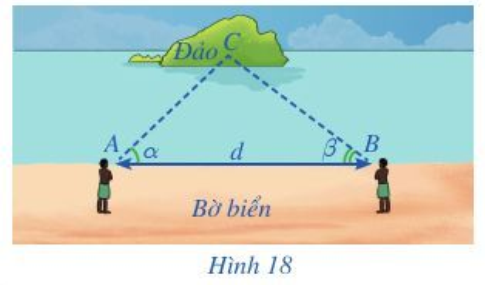
Giải tam giác được hiểu như thế nào?

Lời giải:

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

Hoạt động 1 trang 72 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, $\widehat{A}=\alpha$. Viết công thức tính BC theo b, c, α.

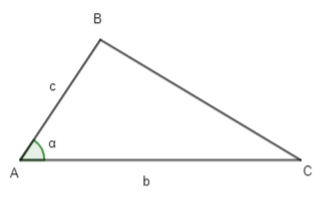
Lời giải:

Áp dụng định lí côsin vào tam giác ABC ta có:

BC² = AB² + AC² – 2.AB.AC.cos A = c² + b² – 2.b.c.cosα

$\Rightarrow BC=\sqrt{c^2+b^2-2bc\cos \alpha }$.

Hoạt động 2 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, BC = a. Viết công thức tính cos A theo a, b, c.

Lời giải:

Áp dụng định lí côsin vào tam giác ABC ta có:

BC² = AB² + AC² - 2.AB.AC.cos A

$\Rightarrow$ cos A = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}$

Vậy cos A = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}$.

Hoạt động 3 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, $\widehat{B}=\alpha$, $\widehat{C}=\beta$. Viết công thức tính AB và AC theo a, α, β

Lời giải:

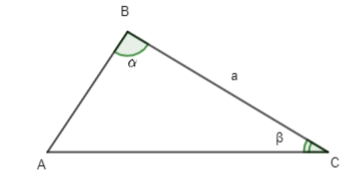
Trong tam giác ABC có: $\widehat{A}=180°-\widehat{B}-\widehat{C}=180°-\alpha -\beta$.

Áp dụng định lí sin vào tam giác ABC ta có:

$\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}$

$\Rightarrow \frac{a}{\sin \left(180°-\alpha -\beta \right)}=\frac{AC}{\sin \alpha }=\frac{AB}{\sin \beta }$

Do đó AC = $\frac{a.\sin \alpha }{\sin \left(180°-\alpha -\beta \right)}$ và AB =$\frac{a.\sin \beta }{\sin \left(180°-\alpha -\beta \right)}$.

Hoạt động 4 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, BC = a. Kẻ đường cao BH.

a) Tính BH theo c và sin A.

b) Tính diện tích S của tam giác ABC theo b, c, và sin A.

Lời giải:

a) Xét các trường hợp: 

+ Với $\widehat{A}<90°$

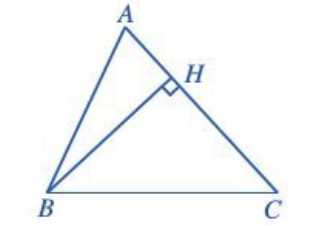
Xét tam giác vuông AHB, ta có $\sin \text{A}=\frac{BH}{BA}$

Do đó BH = AB . sin A = c . sin A.

+ Với $\widehat{A}=90°$

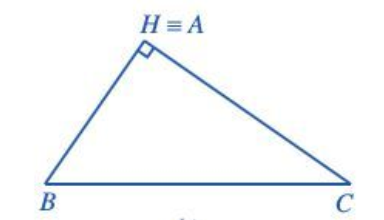
Khi đó sin A = sin 90^o = 1; BH = BA = c . 1 = c . sin A.

+ Với $\widehat{A}>90°$

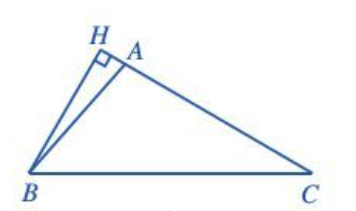
Xét tam giác AHB vuông, ta có: $\widehat{BAH}=180°-\widehat{A}$.

Do đó BH = AB . sin(180° – $\widehat{A}$) = AB . sin A = c . sin A.

Như vậy, trong mọi trường hợp ta đều có BH = c . sin A.

b) Diện tích tam giác ABC bằng $\frac{1}{2}$AC.BH nên $S=\frac{1}{2}AC.BH=\frac{1}{2}bc\sin A$.

Luyện tập 1 trang 74 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 12; $\widehat{B}=60°;\widehat{C}=45°$. Tính diện tích của tam giác ABC.

Lời giải:

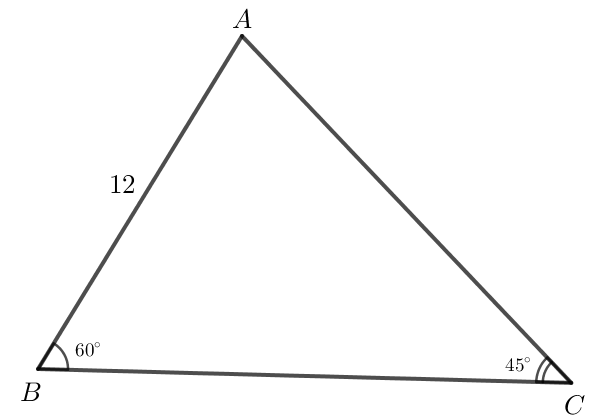
Xét tam giác ABC ta có $\widehat{A}=180°-\widehat{B}-\widehat{C}=180°-60°-45°=75°$.

Áp dụng định lí sin vào tam giác ABC ta có:

$\frac{BC}{\sin \text{A}}=\frac{AB}{\sin C}$

$\Rightarrow \frac{BC}{\sin 75°}=\frac{12}{\sin 45°}$

$\Rightarrow BC=\frac{12}{\sin 45°}.\sin 75°$

$\Rightarrow$ BC = 6 + $6\sqrt{3}$ 

Khi đó diện tích tam giác ABC bằng:

$\frac{1}{2}$AB . BC . sin B = $\frac{1}{2}$. 12 . (6 + $6\sqrt{3}$) . sin 60o ≈ 85,2.

Hoạt động 5 trang 75 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24).

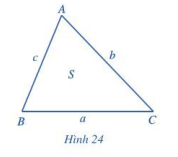
a) Từ định lí côsin, chứng tỏ rằng:

$\sin A=\frac{2}{bc}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$, ở đó $p=\frac{a+b+c}{2}$.

b) Bằng cách sử dụng công thức $S=\frac{1}{2}bc\sin A$, hãy chứng tỏ rằng:

$S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

Lời giải:

a) Xét tam giác ABC, ta có:

BC² = AB² + AC² - 2.AB.AC.cos A (định lí cosin)

$\Rightarrow$ cos A = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}$

$\Rightarrow$ cos A = $\frac{c^2+b^2-a^2}{2.c.b}$

$\Rightarrow {\cos }^{2}A=\frac{{\left(b^2+c^2-a^2\right)}^2}{4b^2{c}^2}$

Do $\widehat{A}$ là góc của tam giác ABC nên $0°<\widehat{A}<180°$.

Do đó sin A > 0.

Lại có cos² A + sin² A = 1 nên sin² A = 1 - cos² A.

$\Rightarrow {\sin }^{2}A=1-\frac{{\left(b^2+c^2-a^2\right)}^2}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{4b^2{c}^2-{\left(b^2+c^2-a^2\right)}^2}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{\left(2bc+b^2+c^2-a^2\right)\left(2bc-b^2-c^2+a^2\right)}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{\left[{\left(b+c\right)}^2-a^2\right]\left[a^2-{\left(b-c\right)}^2\right]}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{\left(b+c+a\right)\left(b+c-a\right)\left(a+b-c\right)\left(a-b+c\right)}{4b^2{c}^2}$

mà $p=\frac{a+b+c}{2}$

$\Rightarrow$ ${\sin }^{2}A=\frac{2p.2\left(p-a\right).2\left(p-c\right).2\left(p-b\right)}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{4p\left(p-a\right)\left(p-b\right)\left(p-c\right)}{b^2{c}^2}$

Do sin A > 0 nên $\sin A=\sqrt{\frac{4p\left(p-a\right)\left(p-b\right)\left(p-c\right)}{b^2{c}^2}}$.

Do đó $\sin A=\frac{2}{bc}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

b) Ta có diện tích tam giác ABC: S = $\frac{1}{2}$bc.sin A.

Mà $\sin A=\frac{2}{bc}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$ nên S = $\frac{1}{2}$bc. $\frac{2}{bc}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

Do đó $S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

Luyện tập 2 trang 76 Toán lớp 10 Tập 1: Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34°, góc lệch giữa phương quan  sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

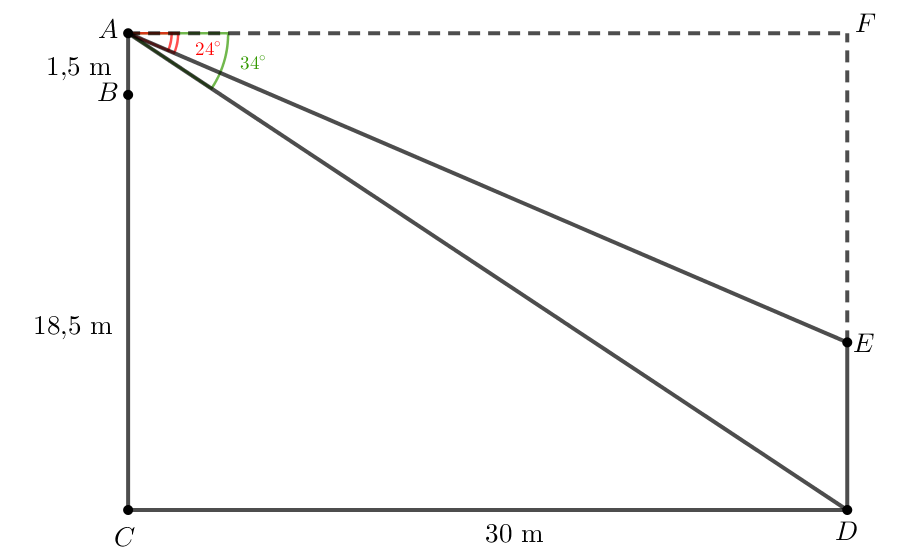
Gọi BC là chiều cao của tòa nhà, AB là chiều cao của chân giác kế, CD là khoảng cách giữa tòa nhà và cái cây, $\widehat{DAF}$ là góc lệch giữa phương quan sát gốc cây và phương nằm ngang, $\widehat{EAF}$ là góc lệch giữa ngọn cây và phương nằm ngang. Khi đó chiều cao của cây là độ dài DE.

Tam giác AFD vuông tại F nên $\tan \widehat{DAF}=\frac{DF}{AF}$

$\Rightarrow$ DF = AF . tan $\widehat{DAF}$ = 30 . tan 34^o ≈ 20,2 m.

Tam giác AFE vuông tại F nên $\tan \widehat{EAF}=\frac{EF}{AF}$

$\Rightarrow$ EF = AF. tan $\widehat{EAF}$ = 30 . tan 24^o ≈ 13,4 m.

Khi đó DE = DF - EF = 20,2 - 13,4 = 6,8 m.

Vậy chiều cao cây khoảng 6,8 m.

Bài tập

Bài 1 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = 12, CA = 15, $\widehat{C}=120°$. Tính:

a) Độ dài cạnh AB;

b) Số đo các góc A, B;

c) Diện tích tam giác ABC.

Lời giải:

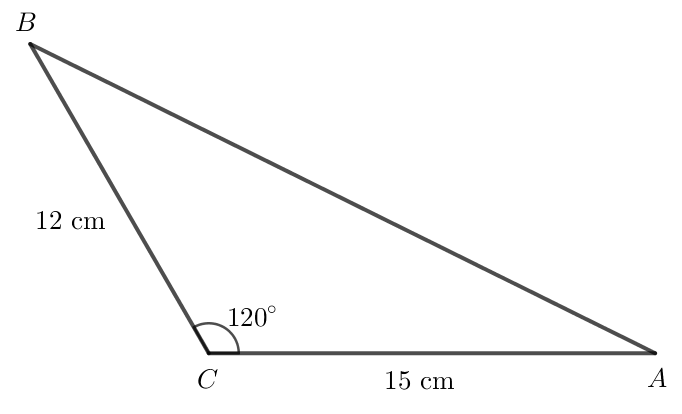
a) Áp dụng định lí côsin vào tam giác ABC có:

AB² = BC² + CA² - 2.BC.CA.cos C

$\Rightarrow$ AB² = 12² + 15² - 2.12.15.cos 120^o

$\Rightarrow$ AB² = 549

$\Rightarrow$ AB = $3\sqrt{61}$ m.

b) Áp dụng định lí sin vào tam giác ABC có:

$\frac{AB}{\sin C}=\frac{AC}{\sin B}$

$\Rightarrow \sin B=\frac{AC.\sin C}{AB}=\frac{15.\sin 120°}{3\sqrt{61}}\approx 0,554$

$\Rightarrow \widehat{B}$ ≈ 34^o.

Trong tam giác ABC có

$$\begin{gathered} \widehat{A}=180°-\widehat{B}-\widehat{C} \\ =180°-34°-120° \\ =26° \end{gathered}$$.

c) Diện tích tam giác ABC là:

S =$\frac{1}{2}$BC.AC.sin C = $\frac{1}{2}$.12.15.sin 120o = $45\sqrt{3}$ (đvdt).

Bài 2 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 5, BC = 7, $\widehat{A}=120°$. Tính độ dài cạnh AC.

Lời giải:

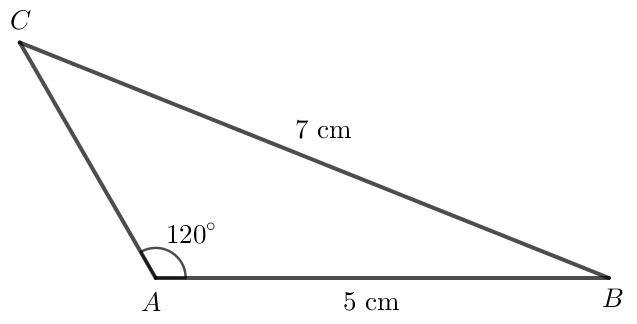
Áp dụng định lí sin vào tam giác ABC có:

$\frac{BC}{\sin \text{A}}=\frac{AB}{\sin C}$

$\Rightarrow \sin C=\frac{AB.\sin \text{A}}{BC}=\frac{5.\sin 120°}{7}=\frac{5\sqrt{3}}{14}$

$\Rightarrow \widehat{C}$ ≈ 38,2^o.

Trong tam giác ABC có

$$\begin{gathered} \widehat{B}=180°-\widehat{A}-\widehat{C} \\ =180°-120°-38,2° \\ =21,8° \end{gathered}$$.

Áp dụng định lí sin vào tam giác ABC có:

$\frac{BC}{\sin \text{A}}=\frac{AC}{\sin B}$

$\Rightarrow AC=\frac{BC.\sin B}{\sin \text{A}}=\frac{7.\sin 21,2°}{\sin 120°}\approx 2,9$ m.

Vậy độ dài cạnh AC là 2,9m.

Bài 3 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 100, $\widehat{B}=100°$, $\widehat{C}=45°$. Tính:

a) Độ dài các cạnh AC, BC;

b) Diện tích tam giác ABC.

Lời giải:

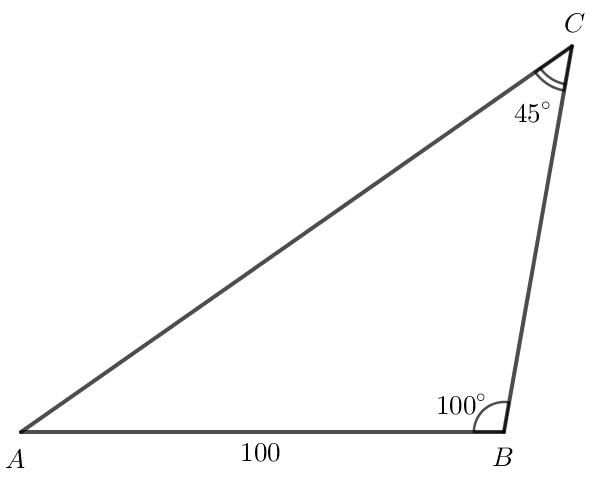
a) Trong tam giác ABC có

$$\begin{gathered} \widehat{A}=180°-\widehat{B}-\widehat{C} \\ =180°-100°-45° \\ =35° \end{gathered}$$.

Áp dụng định lí sin vào tam giác ABC có:$\frac{AC}{\sin B}=\frac{AB}{\sin C}=\frac{BC}{\sin \text{A}}$

Do đó$AC=\frac{AB.\sin B}{\sin C}=\frac{100.\sin 100°}{\sin 45°}\approx 139,3$

$BC=\frac{AB.\sin \text{A}}{\sin C}=\frac{100.\sin 35°}{\sin 45°}\approx 81,1$

Vậy AC ≈ 139,3, BC ≈ 81,1.

b) Diện tích tam giác ABC là:

S = $\frac{1}{2}$. AB.AC.sin A = $\frac{1}{2}$. 100 . 139,3 . sin 35^o ≈ 3995 (đvdt).

Vậy diện tích tam giác ABC là 3995 (đvdt).

Bài 4 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 12, AC = 15, BC = 20. Tính:

a) Số đo các góc A, B, C;

b) Diện tích tam giác ABC.

Lời giải:

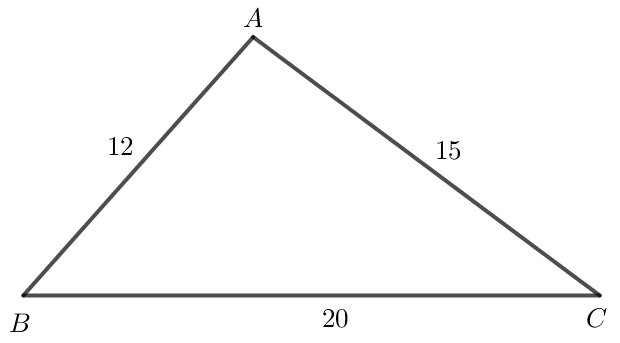
a) Áp dụng hệ quả của định lí côsin vào tam giác ABC ta có:

cos A = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{{12}^2+{15}^2-{20}^2}{\mathrm{2.12.15}}=\frac{-31}{360}$

$\Rightarrow \widehat{A}$ ≈ 95^o.

cos B = $\frac{B{C}^2+B{A}^2-A{C}^2}{2.BC.CA}=\frac{{20}^2+{12}^2-{15}^2}{\mathrm{2.20.12}}=\frac{319}{480}$

$\Rightarrow \widehat{B}$ ≈ 48^o.

Trong tam giác ABC có:

$$\begin{gathered} \widehat{C}=180°-\widehat{A}-\widehat{B} \\ =180°-95°-48°=37° \end{gathered}$$

b) Diện tích tam giác ABC là:

S = $\frac{1}{2}$AB . AC . sin A = $\frac{1}{2}$. 12 . 15 . sin 95^o ≈ 90 (đvdt).

Vậy diện tích tam giác ABC là 90 (đvdt). 

Bài 5 trang 77 Toán lớp 10 Tập 1: Tính độ dài cạnh AB trong mỗi trường hợp sau:

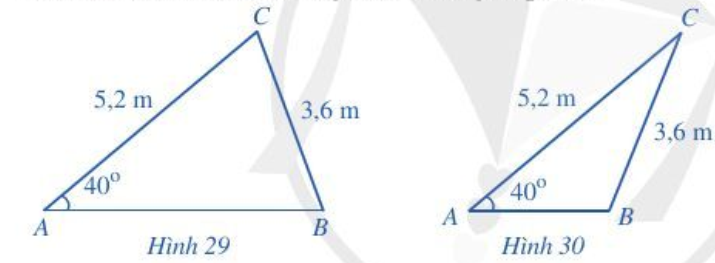
Lời giải:

+) Xét Hình 29:

Áp dụng định lí sin vào tam giác ABC ta có:

$\frac{BC}{\sin \text{A}}=\frac{AC}{\sin B}$

$\Rightarrow \sin B=\frac{AC.\sin \text{A}}{BC}=\frac{5,2.\sin 40°}{3,6}\approx 0,93$

$\Rightarrow \widehat{B}\approx 68°$.

Trong tam giác ABC có $\widehat{C}=180°-\widehat{A}-\widehat{B}=180°-40°-68°=72°$.

Áp dụng định lí sin vào tam giác ABC ta có:

$\frac{BC}{\sin \text{A}}=\frac{AB}{\sin C}$

$\Rightarrow AB=\frac{BC.\sin C}{\sin \text{A}}=\frac{3,6.\sin 72°}{\sin 40°}\approx 5,3$ m.

Vậy AB ≈ 5,3 m.

+) Xét Hình 30:

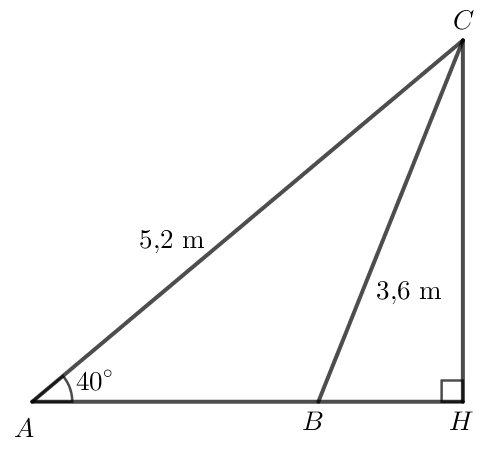
Gọi H là chân đường cao kẻ từ C đến AB.

Tam giác ACH vuông tại H nên $\text{cos\hspace{0.17em}}\widehat{CAH}=\frac{AH}{AC}$.

Do đó AH = AC. cos $\widehat{CAH}$ = 5,2 . cos 40^o ≈ 4 m.

$\text{sin\hspace{0.17em}}\widehat{CAH}=\frac{CH}{AC}\Rightarrow$ CH = AC . sin $\widehat{CAH}$ = 5,2 . sin 40^o ≈ 3,3 m.

Áp dụng định lí Pythagore vào tam giác BCH vuông tại H:

BH² + CH² = BC² $\Rightarrow$ BH² = BC² - CH²

$\Rightarrow$ BH² = 3,6² - 3,3² $\Rightarrow$ BH² = 2,07

$\Rightarrow$ BH ≈ 1,44 m.

Khi đó AB ≈ 4 - 1,44 ≈ 2,56 m.

Vậy AB ≈ 2,56m.

Bài 6 trang 77 Toán lớp 10 Tập 1: Để tính khoảng cách giữa hai địa điểm A và B mà không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và $\widehat{ACB}=105°$ (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

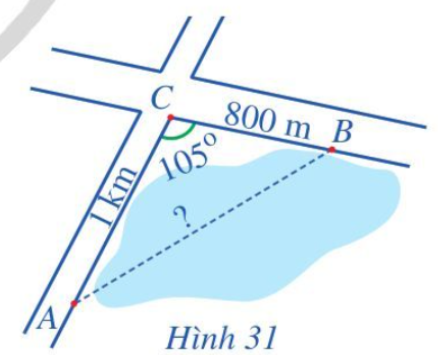
Lời giải:

Đổi 1 km = 1 000 m.

Ba vị trí A, B, C tạo thành ba đỉnh của tam giác.

Áp dụng định lí côsin vào tam giác ABC ta có:

AB² = AC² + BC² - 2.AC.BC.cos C

$\Rightarrow$ AB² = 1 000² + 800² - 2.1000.800.cos 105^o

$\Rightarrow$ AB² ≈ 2 054 110,5 m.

$\Rightarrow$ AB ≈ 1433,2 m.

Vậy AB ≈ 1433,2 m.

Bài 7 trang 77 Toán lớp 10 Tập 1: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45° và 75°. Biết khoảng cách giữa hai bị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

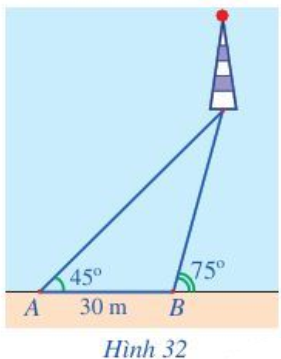
Lời giải:

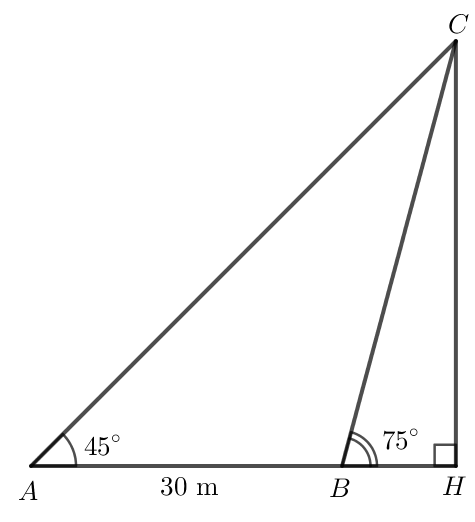
Gọi C là vị trí ngọn hải đăng, khi đó CH là khoảng cách giữa ngọn hải đăng và bờ.

Ta có $\widehat{CBH}$ là góc ngoài tại đỉnh B của tam giác ABC nên $\widehat{CBH}=\widehat{BAC}+\widehat{BCA}$.

Do đó $\widehat{BCA}=\widehat{CBH}-\widehat{BAC}=75°-45°=30°$.

Áp dụng định lí sin vào tam giác ABC có:

$\frac{AB}{\sin C}=\frac{BC}{\sin \text{A}}$

$\Rightarrow BC=\frac{AB.\sin \text{A}}{\sin C}=\frac{30.\sin 45°}{\sin 30°}=30\sqrt{2}$ m.

Trong tam giác CBH vuông tại H:

$\sin \widehat{CBH}=\frac{CH}{BC}$

$\Rightarrow$ CH = BC . sin $\widehat{CBH}$ 

= $30\sqrt{2}$ . sin 75^o = 15 + $15\sqrt{3}$ m ≈ 41 m.

Vậy khoảng cách từ ngọn hải đăng đến bờ khoảng 41 m.