Giải Toán 10 (Cánh diều) Bài 5: Tích của một số với một vectơ
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 10 Bài 5: Tích của một số với một vectơ sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 5. Mời các bạn đón xem:
Giải bài tập Toán 10 Bài 5: Tích của một số với một vectơ
Khởi động trang 88 Toán lớp 10 Tập 1: Hai đoàn tàu chạy song song (Hình 58). Gọi →v1, →v2 lần lượt là các vectơ mô tả vận tốc của hai đoàn tàu.

Mối liên hệ giữa hai vectơ vận tốc →v1, →v2 là như thế nào?
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ta thấy hai vectơ →v1, →v2 là hai vectơ cùng phương nên →v1=k→v2 với k ≠ 0.
Hoạt động 1 trang 88 Toán lớp 10 Tập 1: Gọi B là trung điểm của AC.
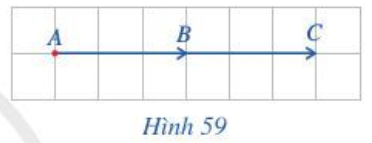
Chứng tỏ rằng →AC=→AB+→AB.
Lời giải:
Do B là trung điểm của AC nên →BC=→AB.
Do đó →AB+→BC=→AB+→AB hay →AC=→AB+→AB.
Hoạt động 2 trang 88 Toán lớp 10 Tập 1: Gọi B là trung điểm của AC.
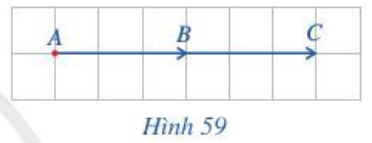
Quan sát vectơ →AB và →AC, nêu mối liên hệ về hướng và độ dài của vectơ 2→AB với →AB.
Lời giải:
Từ Hoạt động khám phá 1, ta có:
Mặt khác: →AB+→AB=2→AB nên →AC= 2→AB.
Do đó vectơ cùng hướng với vectơ và |→AC|=|2→ AB|.
Quan sát trên Hình 59, ta cũng thấy vectơ cùng hướng với vectơ →AB và độ dài vectơ bằng 2 lần độ dài vectơ →AB. Do đó vectơ 2→AB cùng hướng với →AB và |2→AB|=2|→AB|.
Luyện tập 1 trang 89 Toán lớp 10 Tập 1: Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G. Tìm các số a, b biết: →AG=a→AM; →GN=b→GB.
Lời giải:
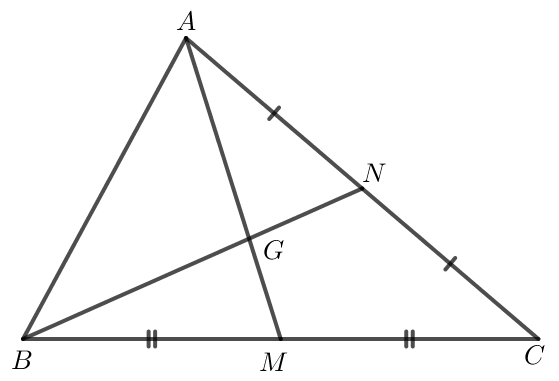
Tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Do đó AG = 23AM; GN = 12GB.
Vì AM là đường trung tuyến nên G thuộc đoạn AM
Do →AG và →AM là hai vectơ cùng hướng nên →AG=23→AM.
Vì BN là đường trung tuyến nên G thuộc đoạn BN.
Do →GN và →GB là hai vectơ cùng hướng nên →GN=12→GB.
Vậy a = 23; b = 12.
Luyện tập 2 trang 89 Toán lớp 10 Tập 1: Cho ba điểm A, B, C. Chứng minh 3(→AB+2→BC)−2(→AB+3→BC)=→AB.
Lời giải:
3(→AB+2→BC)−2(→AB+3→BC)
=3→AB+6→BC−2→AB−6→BC
=3→AB−2→AB+6→BC−6→BC
=→AB
Vậy 3(→AB+2→BC)−2(→AB+3→BC)=→AB.
Hoạt động 3 trang 90 Toán lớp 10 Tập 1: Cho I là trung điểm của đoạn thẳng AB và điểm M tùy ý. Chứng minh rằng →MA+→MB=2→MI.
Lời giải:
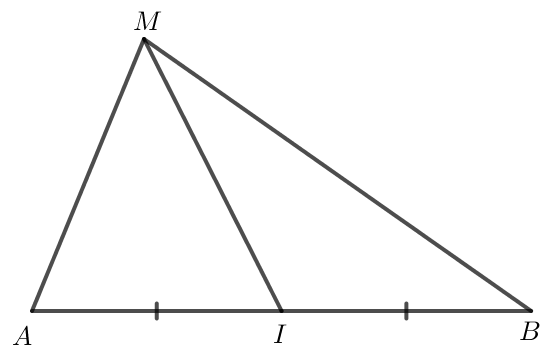
Ta có →MA=→MI+→IA; →MB=→MI+→IB.
Do đó →MA+→MB=→MI+→IA+→MI+→IB=2→MI+→IA+→IB.
Do I là trung điểm của AB nên →IA=−→IB.
Do đó 2→MI+→IA+→IB=2→MI−→IB+→IB=2→MI.
Vậy →MA+→MB=2→MI.
Hoạt động 4 trang 90 Toán lớp 10 Tập 1: Cho G là trọng tâm của tam giác ABC và điểm M tùy ý. Chứng minh rằng →MA+→MB+→MC=3→MG.
Lời giải:
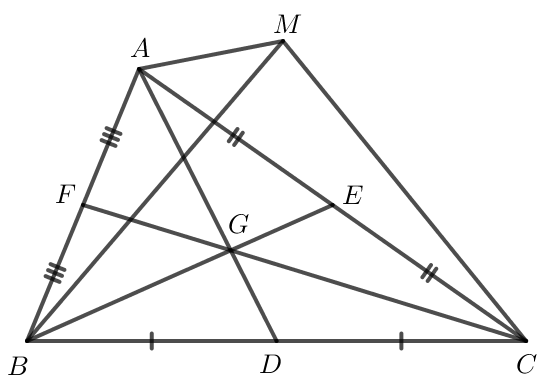
Gọi D, E, F lần lượt là trung điểm của BC, AC, AB.
Do D là trung điểm của BC nên →AB+→AC=2→AD.
Do E là trung điểm của AC nên →BA+→BC=2→BE.
Do F là trung điểm của AB nên →CA+→CB=2→CF.
Do đó →AB+→AC+→BA+→BC+→CA+→CB=2→AD+2→BE+2→CF.
⇒→AB+→BA+→AC+→CA+→BC+→CB=2→AD+2→BE+2→CF.
⇒2→AD+2→BE+2→CF=→0
⇒→AD+→BE+→CF=→0
⇒−(→AD+→BE+→CF)=→0
⇒−→AD−→BE−→CF=→0
⇒→DA+→EB+→FC=→0
Do G là trọng tâm của tam giác ABC nên
→GA=23→DA; →GB=23→EB; →GC=23→FC.
Do đó →GA+→GB+→GC=23(→DA+→EB+→FC)=→0.
Ta có →MA+→MB+→MC=→MG+→GA+→MG+→GB+→MG+→GC
=3→MG+(→GA+→GB+→GC)
=3→MG
Vậy →MA+→MB+→MC=3→MG.
Luyện tập 3 trang 90 Toán lớp 10 Tập 1: Cho tam giác ABC có G là trọng tâm. Chứng minh →AB+→AC=3→AG.
Lời giải:
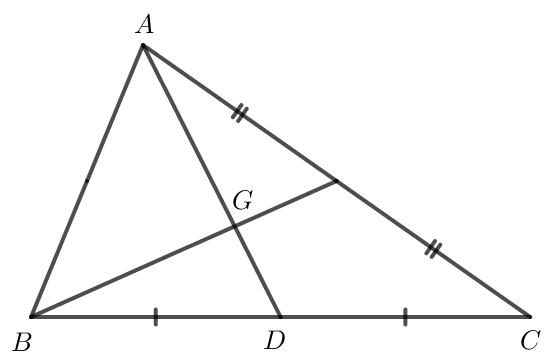
Gọi D là trung điểm của BC.
Do D là trung điểm của BC nên →AB+→AC=2→AD.
Do G là trọng tâm của tam giác ABC nên →AG=23→AD hay →AD=32→AG.
Do đó →AB+→AC=2→AD=2.32→AG=3→AG.
Vậy →AB+→AC=3→AG.
Hoạt động 5 trang 91 Toán lớp 10 Tập 1: Cho hai vectơ →a và →b khác →0 sao cho →a=k→b với k là số thực khác 0. Nêu nhận xét về phương của hai vectơ →a và →b.
Lời giải:
Ta có →a=k→b với k là số thực khác 0. Khi đó hai vectơ →a và →b cùng phương.
Hoạt động 6 trang 91 Toán lớp 10 Tập 1: Cho ba điểm phân biệt A, B, C.
a) Nếu ba điểm A, B, C thẳng hàng thì hai vectơ →AB, →AC có cùng phương hay không?
b) Ngược lại, nếu hai vectơ →AB, →AC cùng phương thì ba điểm A, B, C có thẳng hàng hay không?
Lời giải:
a) Giá của vectơ →AB là đường thẳng AB, giá của vectơ →AC là đường thẳng AC.
Do A, B, C thẳng hàng nên đường thẳng AB trùng với đường thẳng AC.
Do đó hai vectơ →AB, →AC cùng phương.
b) Giá của vectơ →AB là đường thẳng AB, giá của vectơ →AC là đường thẳng AC.
Hai vectơ →AB, →AC cùng phương nên giá của chúng song song hoặc trùng nhau.
Mà AB và AC có điểm chung là A nên AB trùng AC.
Do đó A, B, C thẳng hàng.
Luyện tập 4 trang 91 Toán lớp 10 Tập 1: Ở Hình 61, tìm k trong mỗi trường hợp sau:
a) →AC=k→AD,
b) →BD=k→DC.
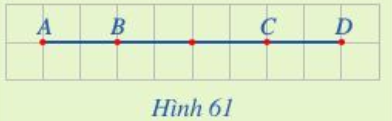
Lời giải:
a) Hai vectơ →AC và →AD là hai vectơ cùng hướng và AC = 34AD nên →AC=34→AD.
Vậy k = 34.
b) Hai vectơ →BD và →DC là hai vectơ ngược hướng và BD = 3DC nên →BD=−3→DC.
Vậy k = -3.
Bài tập
Bài 1 trang 92 Toán lớp 10 Tập 1: Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?
A. →MN=2→PQ;
B. →MQ=2→NP;
C. →MN=−2→PQ;
D. →MQ=−2→NP.
Lời giải:
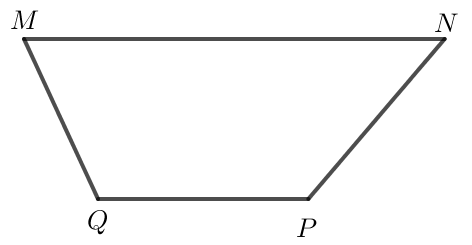
Ta thấy hai vectơ →MN và →PQ là hai vectơ ngược hướng và MN = 2PQ nên →MN=−2→PQ.
Vậy đáp án đúng là đáp án C.
Bài 2 trang 92 Toán lớp 10 Tập 1: Cho đoạn thẳng AB = 6 cm.
a) Xác định điểm C thỏa mãn →AC=12→AB.
b) Xác định điểm D thỏa mãn →AD=−12→AB.
Lời giải:
a) Ta thấy 12 > 0 nên hai vectơ →AC và →AB cùng hướng.
Khi đó |→AC|=12|→AB| hay AC = 12AB và A, B, C thẳng hàng.
Do đó C là trung điểm của AB.
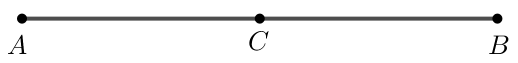
b) Ta thấy −12<0 nên hai vectơ →AD và →AB ngược hướng.
Khi đó |→AD|=|−12||→AB| hay AD = 12AB và A, B, D thẳng hàng.
Do đó D nằm khác phía với B so với điểm A sao cho AD = 12AB.

Bài 3 trang 92 Toán lớp 10 Tập 1: Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh:
a) →AP+12→BC=→AN;
b) →BC+2→MP=→BA.
Lời giải:
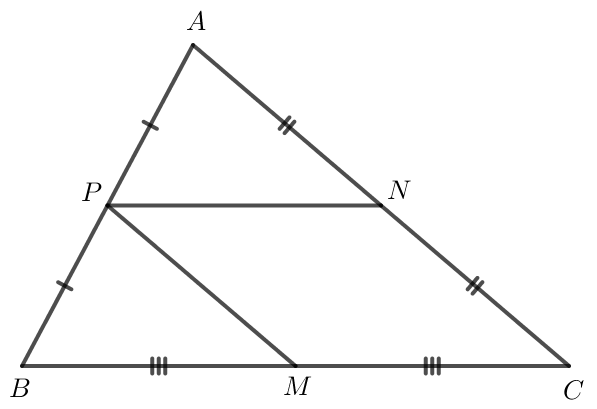
a) Tam giác ABC có P là trung điểm của AB; N là trung điểm của AC nên PN là đường trung bình của tam giác ABC.
Do đó PN // BC và PN = 12BC.
Ta thấy hai vectơ →PN và →BC cùng hướng và PN = 12BC nên →PN=12→BC.
Do đó →AP+12→BC=→AP+→PN=→AN.
Vậy →AP+12→BC=→AN.
b) Tam giác ABC có P là trung điểm của AB; M là trung điểm của BC nên PM là đường trung bình của tam giác ABC.
Do đó MP // CA và MP = 12CA.
Ta thấy hai vectơ →MP và →CA cùng hướng và MP = 12CA nên →MP=12→CA hay →CA=2→MP.
Do đó →BC+2→MP=→BC+→CA=→BA.
Vậy →BC+2→MP=→BA.
Bài 4 trang 92 Toán lớp 10 Tập 1: Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62). Giả sử →AB=→a, →AC=→b. Biểu diễn các vectơ →BC,→BD, →BE, →AD, →AE theo →a, →b.
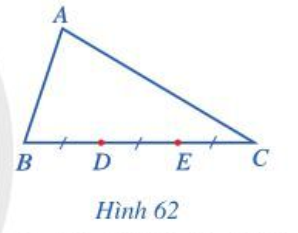
Lời giải:
Ta có →BC=→AC−→AB=→b−→a;
Do BD = DE = EC và BD + DE + EC = BC nên BD = DE = EC = 13BC.
Hai vectơ →BD và →BC cùng hướng và BD = 13BC nên →BD=13→BC=13(→b−→a)=→b−→a3.
Hai vectơ →BE và →BD cùng hướng và BE = 2BD nên →BE=2→BD=23(→b−→a)=2→b−2→a3.
Có →AB+→BD=→AD nên →AD=→a+→b−→a3=3→a+→b−→a3=2→a+→b3.
Có →AB+→BE=→AE nên →AE=→a+2→b−2→a3=3→a+2→b−2→a3=→a+2→b3.
Bài 5 trang 92 Toán lớp 10 Tập 1: Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm của tam giác BCD. Chứng minh:
a) →EA+→EB+→EC+→ED=4→EG;
b) →EA=4→EG;
c) Điểm G thuộc đoạn thẳng AE và →AG=34→AE.
Lời giải:
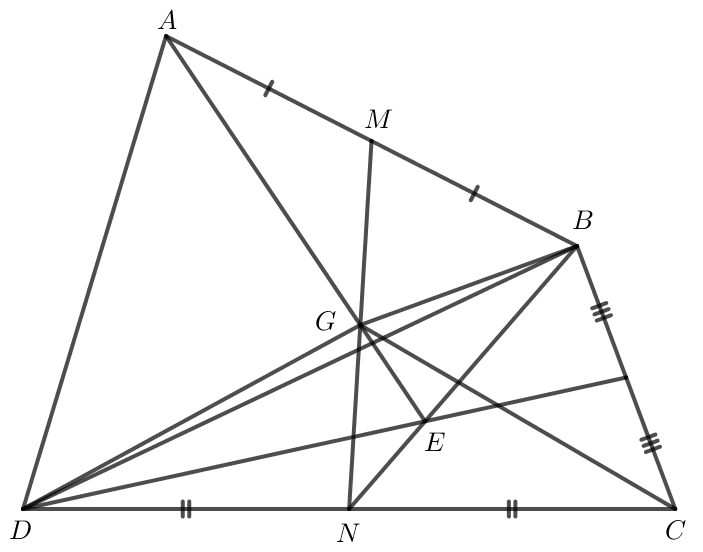
a) Do M là trung điểm của AB nên →GA+→GB=2→GM (1).
Do N là trung điểm của CD nên →GC+→GD=2→GN (2).
Do G là trung điểm của MN nên GM = GN.
Ta thấy hai vectơ →GM và →GN ngược hướng và GM = GN nên →GM=−→GN.
Do đó →GM+→GN=−→GN+→GN=→0.
Từ (1) và (2) ta có →GA+→GB+→GC+→GD=2→GM+2→GN=2(→GM+→GN)=→0.
Ta có
→EA+→EB+→EC+→ED=→EG+→GA+→EG+→GB+→EG+→GC+→EG+→GD
=4→EG+(→GA+→GB+→GC+→GD)
=4→EG
Vậy →EA+→EB+→EC+→ED=4→EG.
b) Do E là trọng tâm của tam giác BCD nên →EB+→EC+→ED=→0.
Do đó →EA=4→EG.
c) Do →EA=4→EG nên hai vectơ →EA và →EG cùng hướng.
Mà 4 > 0 nên G nằm giữa A và E.
Do đó |→EA|=4|→EG| hay EA = 4EG.
⇒ EG = 14EA
⇒ AG = 34EA.
Ta thấy hai vectơ →AG và →AE cùng hướng và AG = 34EA nên →AG=34→AE.
Bài 6 trang 92 Toán lớp 10 Tập 1: Cho hình bình hành ABCD. Đặt →AB=→a, →AD=→b. Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ →AG, →CG theo hai vectơ →a, →b.
Lời giải:
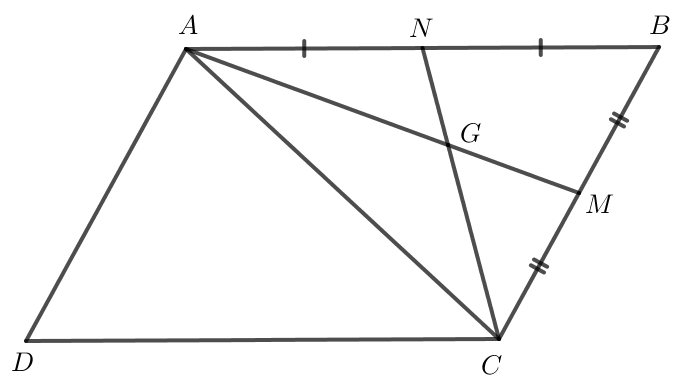
Gọi M và N lần lượt là trung điểm của BC và AB.
Do ABCD là hình bình hành nên →AD=→BC=→b.
Do M là trung điểm của BC nên BM = 12BC.
Hai vectơ →BM và →BC cùng hướng và BM = 12BC nên →BM=12→BC=→b2.
Do N là trung điểm của AB nên NB = 12AB.
Hai vectơ →BN và →AB ngược hướng và NB = 12AB nên →BN=−12→AB=−→a2.
Ta có →AM=→AB+→BM=→a+→b2; →CN=→CB+→BN=−→b−→a2.
Do G là trọng tâm của tam giác ABC nên →AG=23→AM và →CG=23→CN.
Do đó →AG=23(→a+→b2)=23→a+13→b và →CG=23(−→b−→a2)=−23→b−13→a.
Bài 7 trang 92 Toán lớp 10 Tập 1: Cho tam giác ABC. Các điểm D, E, H thỏa mãn
→DB=13→BC, →AE=13→AC,→AH=23→AB.
a) Biểu thị mỗi vectơ →AD, →DH, →HE theo hai vectơ →AB, →AC.
b) Chứng minh D, E, H thẳng hàng.
Lời giải:
Vì →DB=13→BC nên →DB và →BC cùng hướng và DB=13BC.
→AE=13→AC nên →AE, →AC cùng hướng và AE = 13AC.
→AH=23→AB nên →AH, →AB cùng hướng và AH=23AB.
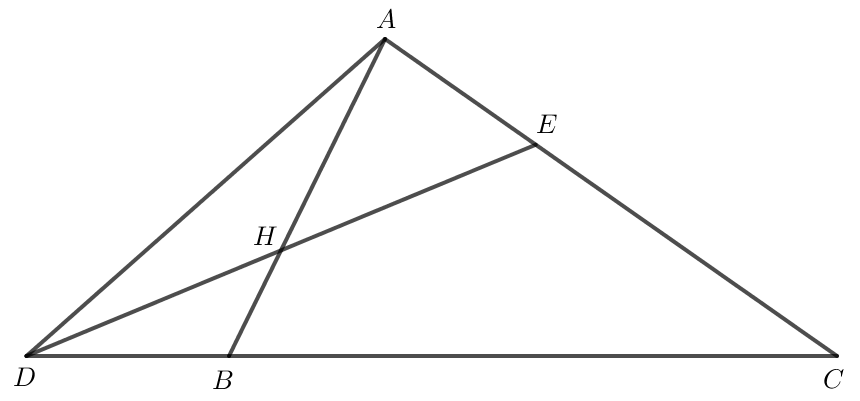
a) Do →DB=13→BC nên →BD=−13→BC=−13(→BA+→AC)=−13(−→AB+→AC)=→AB3−→AC3.
Ta có: →AD=→AB+→BD=→AB+→AB3−→AC3=43→AB−13→AC.
→DH=→DB+→BH=13→BC+13→BA=13(→BA+→AC)+13→BA
=23→BA+13→AC=−23→AB+13→AC.
→HE=→AE−→AH=13→AC−23→AB=−23→AB+13→AC.
b) Từ phần a ta thấy →DH=→HE=−23→AB+13→AC.
Do đó D, H, E thẳng hàng và H là trung điểm của DE.


