Giải bài tập Toán 10: Bài tập cuối chương 5 

Bài 1 trang 20 Toán 10 Tập 2:

a) Có bao nhiêu cách xếp 20 học sinh theo một hàng dọc?

A. 20²⁰.

B. 20!.

C. 20.

D. 1.

b) Số cách chọn ra 3 học sinh từ một lớp có 40 học sinh là:

A. $A_{40}^3$.

B. 40³.

C. 3⁴⁰.

D. $C_{40}^3$.

Lời giải

a) Đáp án đúng là: B. 

Mỗi cách xếp 20 học sinh theo một hàng dọc là một hoán vị của 20 phần tử, vậy có 20! cách xếp 20 học sinh theo một hàng dọc.

b) Đáp án đúng là: D.

Mỗi cách chọn 3 học sinh từ 40 học sinh là một tổ hợp chập 3 của 40, vậy có $C_{40}^3$ cách chọn 3 học sinh từ 40 học sinh.

Bài 2 trang 20 Toán 10 Tập 2: Bạn Dương có 2 chiếc quần gồm: một quần màu xanh và một quần màu đen; 3 chiếc áo gồm: một áo màu nâu, một áo màu xanh và một áo màu vàng; 2 đôi giày gồm: một đôi giày màu đen và một đôi giày màu đỏ. Bạn Dương muốn chọn một bộ quần áo và một đôi giày để đi tham quan. Bằng cách vẽ sơ đồ hình cây, tính số cách chọn một bộ quần áo và một đôi giày cho bạn Dương.

Lời giải

Theo bài ra ta có sơ đồ hình cây:

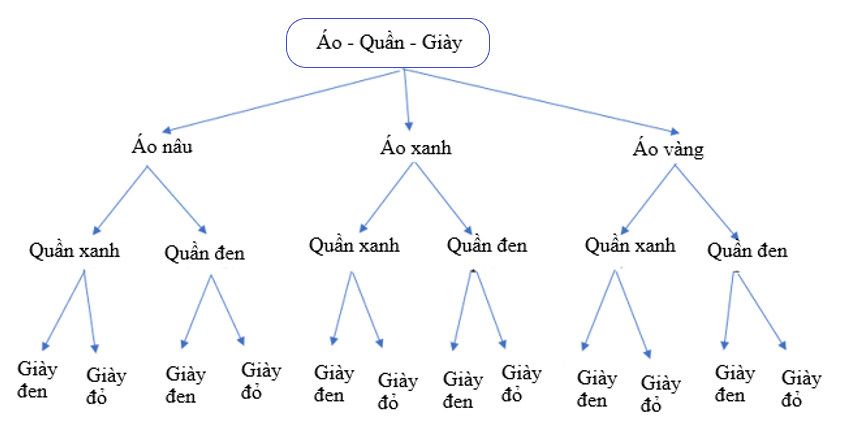
Từ sơ đồ trên ta thấy, có 12 cách chọn một bộ quần áo và một đôi giày cho bạn Dương.

Bài 3 trang 20 Toán 10 Tập 2: Trong mặt phẳng, cho hai đường thẳng song song a và b. Cho 3 điểm phân biệt trên đường thẳng a và 4 điểm phân biệt trên đường thẳng b. Có bao nhiêu tam giác có cả 3 đỉnh là 3 điểm trong 7 điểm nói trên?

Lời giải

Chọn 3 điểm để tạo thành 3 đỉnh của một tam giác thì 3 điểm đó phải không thẳng hàng.

Vậy ta chọn 3 điểm sao cho 1 điểm thuộc được thẳng này và 2 điểm còn lại thuộc đường thẳng kia. Khi chọn như trên, ta chỉ có thể chọn theo một trong hai khả năng sau:

+ Chọn 1 điểm thuộc đường thẳng a và 2 điểm thuộc đường thẳng b;

+ Chọn 2 điểm thuộc đường thẳng a và 1 điểm thuộc đường thẳng b.

• Xét khả năng thứ nhất: Chọn 1 điểm thuộc đường thẳng a và 2 điểm thuộc đường thẳng b.

- Chọn 1 điểm trong 3 điểm thuộc đường thẳng a, có $C_3^1=3$ (cách chọn).

- Chọn 2 điểm trong 4 điểm thuộc đường thẳng b, có $C_4^2=6$ (cách chọn).

Theo quy tắc nhân, số cách chọn 1 điểm thuộc đường thẳng a và 2 điểm thuộc đường thẳng b là: 3 . 6 = 18 (cách chọn).

• Xét khả năng thứ hai: Chọn 2 điểm thuộc đường thẳng a và 1 điểm thuộc đường thẳng b.

- Chọn 2 điểm trong 3 điểm thuộc đường thẳng a, có $C_3^2=3$ (cách chọn).

- Chọn 1 điểm trong 4 điểm thuộc đường thẳng b, có $C_4^1=4$ (cách chọn).

Theo quy tắc nhân, số cách chọn 2 điểm thuộc đường thẳng a và 1 điểm thuộc đường thẳng b là: 3 . 4 = 12 (cách chọn).

Vì hai khả năng hay hai trường hợp trên là rời nhau.  

Theo quy tắc cộng, vậy số tam giác có cả 3 đỉnh là 3 điểm trong 7 điểm nói trên là 18 + 12 = 30 (tam giác).

Bài 4 trang 20 Toán 10 Tập 2: Trong mặt phẳng, cho 6 đường thẳng song song và 8 đường thẳng song song cùng vuông góc với 6 đường thẳng đó. Có bao nhiêu hình chữ nhật được tạo thành?

Lời giải

Để tạo được một hình chữ nhật ta cần lấy 2 đường thẳng trong nhóm 6 đường thẳng song song và lấy 2 đường thẳng trong nhóm 8 đường thẳng song song cùng vuông góc với 6 đường thẳng trên.

Nên việc lập một hình chữ nhật được thực hiện bởi 2 hành động liên tiếp:

- Hành động 1: Chọn 2 đường thẳng trong 6 đường thẳng có $C_6^2=15$ cách chọn.

- Hành động 2: Chọn 2 đường thẳng trong 8 đường thẳng có $C_8^2=28$ cách chọn.

Theo quy tắc nhân, vậy số hình chữ nhật được tạo thành là: 15 . 28 = 420 (hình chữ nhật).

Bài 5 trang 20 Toán 10 Tập 2: Khai triển các biểu thức sau: 

a) (4y – 1)⁴;

b) (3x + 4y)⁵.

Lời giải

Áp dụng công thức nhị thức Newton, ta thực hiện như sau:

a) (4y – 1)⁴ 

= [4y + (– 1)]⁴ 

= (4y)⁴ + 4 . (4y)³ . (– 1) + 6 . (4y)² . (– 1)² + 4 . (4y) . (– 1)³ + (– 1)⁴

= 256y⁴ – 256y³ + 96y² – 16y + 1.

b) (3x + 4y)⁵ 

= (3x)⁵ + 5 . (3x)⁴ . (4y) + 10 . (3x)³ . (4y)² + 10 . (3x)² . (4y)³ + 5 . (3x) . (4y)⁴ + (4y)⁵

= 243x⁵ + 1620x⁴y + 4320x³y² + 5760x²y³ + 3840xy⁴ + 1024y⁵.

Bài 6 trang 20 Toán 10 Tập 2: Mật khẩu của máy tính là một dãy các kí tự (có kể thứ tự từ trái qua phải) được chọn từ: 10 chữ số, 26 chữ cái in thường, 26 chữ cái in hoa và 10 kí tự đặc biệt. Bạn Ngân muốn lập một mật khẩu của máy tính có độ dài là 8 kí tự bao gồm: 4 kí tự đầu tiên là 4 chữ số đôi một khác nhau, 2 kí tự tiếp theo là chữ cái in thường, 1 kí tự tiếp theo nữa là chữ cái in hoa, kí tự cuối cùng là kí tự đặc biệt. Bạn Ngân có bao nhiêu cách lập một mật khẩu của máy tính?

Lời giải

Việc lập một mật khẩu máy tính gồm 8 kí tự là việc thực hiện liên tiếp các hành động sau:

- Hành động 1: Chọn 4 kí tự đầu tiên bằng cách lập 4 chữ số đôi một khác nhau trong 10 chữ số, mỗi cách chọn 4 chữ số khác nhau trong 10 chữ số, có xếp thứ tự là một chỉnh hợp chập 4 của 10 phần tử, do đó có $A_{10}^4=5040$ cách chọn.

- Hành động 2: Chọn 2 kí tự tiếp theo là chữ cái in thường, vì 2 kí tự này không nhất thiết khác nhau, nên ta chọn lần lượt từng kí tự, mỗi kí tự có 26 cách chọn. Do đó, chọn 2 kí tự tiếp theo là chữ in thường có 26 . 26 = 676 cách chọn.

- Hành động 3: Chọn 1 kí tự tiếp theo là chữ cái in hoa, chọn 1 chữ trong 26 chữ đó, có 26 cách chọn.

- Hành động 4: Chọn 1 kí tự cuối cùng là kí tự đặc biệt, chọn 1 trong 10 kí tự đặc biệt đó, có 10 cách chọn.

Theo quy tắc nhân, vậy số cách lập một mật khẩu máy tính của bạn Ngân là:

5040 . 676 . 26 . 10 = 885 830 400 (cách lập).

Vậy bạn Ngân có 885 830 400 cách lập một mật khẩu máy tính.

Bài 7 trang 20 Toán 10 Tập 2: Một trường trung học phổ thông tổ chức cuộc thi chạy tiếp sức giữa các lớp với nội dung 4 × 100 m và yêu cầu mỗi đội gồm 2 nam, 2 nữ. Bạn An được giáo viên giao nhiệm vụ chọn ra 4 bạn và sắp xếp thứ tự chạy của các bạn đó để đăng kí dự thi. Bạn An có bao nhiêu cách lập ra một đội thi đủ điều kiện đăng kí? Biết lớp bạn An có 22 nam và 17 nữ.

Lời giải

Để lập ra một đội thi đủ điều kiện đăng kí, ta thực hiện liên tiếp ba hành động sau:

- Hành động 1: Chọn ra 2 bạn nam trong 22 bạn nam có $C_{22}^2=231$ cách chọn.

- Hành động 2: Chọn ra 2 bạn nữ trong 17 bạn nữ có $C_{17}^2=136$ cách chọn.

- Hành động 3: Sắp xếp thứ tự chạy của 4 bạn được chọn ra có 4! = 24 cách xếp.

Theo quy tắc nhân, số cách lập một đội thi đủ điều kiện đăng kí là

231 . 136 . 24 = 753 984 (cách).

Vậy có 753 984 cách lập đội thi thỏa mãn yêu cầu bài toán.

Bài 8 trang 20 Toán 10 Tập 2: Bác Thảo muốn mua 2 chiếc máy tính để phục vụ công việc. Người bán hàng giới thiệu cho bác 3 hãng máy tính để tham khảo: hãng thứ nhất có 4 loại máy tính phù hợp, hãng thứ hai có 5 loại máy tính phù hợp, hãng thứ ba có 7 loại máy tính phù hợp. Bác Thảo có bao nhiêu cách chọn 2 máy tính dùng cho công việc?

Lời giải

Tổng số loại máy tính của cả 3 hãng được giới thiệu cho bác Thảo là: 

4 + 5 + 7 = 16 (máy tính).

Mỗi cách chọn ra 2 máy tính để phục vụ cho công việc là một tổ hợp chập 2 của 16 phần tử nên có $C_{16}^2=120$ cách chọn.

Vậy bác Thảo có 120 cách chọn 2 máy tính dùng cho công việc.