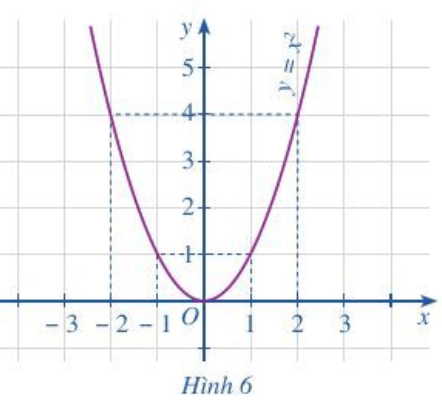
Cho đồ thị hàm số: y = f(x) = x^2 như Hình 6
Lời giải Hoạt động 6 trang 36, 37 Toán lớp 10 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 10 Tập 1.
Giải Toán lớp 10 Bài 1: Hàm số và đồ thị
Hoạt động 6 trang 36, 37 Toán lớp 10 Tập 1: Cho đồ thị hàm số: y = f(x) = x2 như Hình 6.
a) So sánh f(– 2), f(– 1). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ – 2 đến – 1.
b) So sánh f(1), f(2). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ 1 đến 2.
Lời giải:
a) Tại điểm x = -2 trên trục hoành dóng một đường thẳng đứng vuông góc với trục Ox cắt đồ thị tại điểm có tọa độ (-2; 4) nên f(-2) = 4.
Tại điểm x = -1 dóng một đường thẳng vuông góc với trục Ox cắt đồ thị tại điểm có tọa độ (-1; 1) nên f(-1) = 1.
Vì 4 > 1 nên f(– 2) > f(– 1).
Nhận xét về sự biến thiên của giá trị hàm số:
Khi giá trị biến x tăng dần từ – 2 đến – 1 thì giá trị của hàm số giảm dần từ 4 xuống 1.
b) Tại điểm x = 1 trên trục hoành dóng một đường thẳng đứng vuông góc với trục Ox cắt đồ thị tại điểm có tọa độ (1; 1) nên f(1) = 1.
Tại điểm x = 2 dóng một đường thẳng vuông góc với trục Ox cắt đồ thị tại điểm có tọa độ (2; 4) nên f(2) = 4.
Vì 1 < 4 nên f(1) < f(2).
Nhận xét về sự biến thiên của giá trị hàm số:
Khi giá trị biến x tăng dần từ 1 đến 2 thì giá trị của hàm số tăng dần từ 1 lên 4.
Bài viết liên quan
- Giải Toán 10 (Cánh diều) Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
- Giải Toán 10 (Cánh diều) Bài 3: Dấu của tam thức bậc hai
- Giải Toán 10 (Cánh diều) Bài 4: Bất phương trình bậc hai một ẩn
- Giải Toán 10 (Cánh diều) Bài 5: Hai dạng phương trình quy về phương trình bậc hai
- Giải Toán 10 (Cánh diều) Bài tập cuối chương 3
