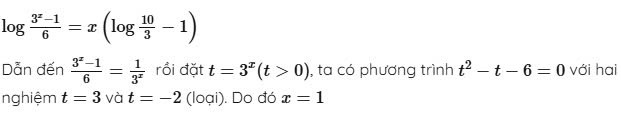x + log(3ˣ - 1) = xlog10/3 + log6

Lê Huy Hỏi từ APP VIETJACK

đã hỏi trong Lớp 11 Toán học

· 20:49 12/04/2025

Trả Lời

Hỏi chi tiết

Trả lời trong APP VIETJACK

Quảng cáo

2 câu trả lời 41

Thúy Vân

1 tuần trước

Ta biến đổi phương trình về dạng:

Hỏi đáp VietJack

0 bình luận

Đăng nhập để hỏi chi tiết

Ngọc

1 tuần trước

x + log(3ˣ - 1) = xlog10/3 + log6

Áp dụng quy tắc lôgarit cho log(10/3):

Vậy, log(10/3) = log(10) - log(3)

Vì log(10) = 1 (do 10¹ = 10), nên:

log(10/3) = 1 - log(3)
thay pt ta có

x + log(3ˣ - 1) = x(1 - log(3)) + log(6)

x + log(3ˣ - 1) = x - xlog(3) + log(6)

Chuyển các hạng tử chứa x về một vế và các hạng tử lôgarit về vế còn lại:

x - (x - xlog(3)) = log(6) - log(3ˣ - 1)

x - x + xlog(3) = log(6) - log(3ˣ - 1)

xlog(3) = log(6) - log(3ˣ - 1)

xlog(3) + log(3ˣ - 1) = log(6)

Áp dụng quy tắc lũy thừa của lôgarit

log(3ˣ) + log(3ˣ - 1) = log(6)

Áp dụng quy tắc tích của lôgarit

log(3ˣ * (3ˣ - 1)) = log(6)

Vì hai lôgarit (cùng cơ số 10) bằng nhau, nên biểu thức bên trong dấu lôgarit cũng phải bằng nhau:

3ˣ * (3ˣ - 1) = 6

Đặt ẩn phụ: Đặt y = 3ˣ (với điều kiện y > 0 vì 3ˣ luôn dương). Phương trình trở thành:

y * (y - 1) = 6

y² - y = 6

y² - y - 6 = 0

Giải phương trình bậc hai: Phân tích thành nhân tử:

(y - 3)(y + 2) = 0

Phương trình này có hai nghiệm:

y = 3 hoặc y = -2

Thay y = 3ˣ trở lại:

Trường hợp 1: 3ˣ = 3 Vì 3¹ = 3, nên x = 1.

Trường hợp 2: 3ˣ = -2 Phương trình này vô nghiệm vì 3ˣ luôn lớn hơn 0 với mọi x.

Kiểm tra điều kiện xác định: Phương trình ban đầu chứa log(3ˣ - 1). Biểu thức trong lôgarit phải lớn hơn 0:

3ˣ - 1 > 0

3ˣ > 1

3ˣ > 3⁰

x > 0

Nghiệm x = 1 thỏa mãn điều kiện x > 0.
=>

Nghiệm duy nhất của phương trình là x = 1.

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

2 câu trả lời 41

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 11