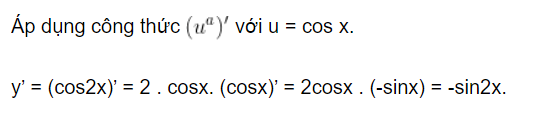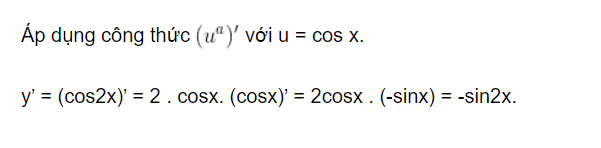Tính đạo hàm của hàm số sau: y = cos2x
A: 2 cosx.sinx
B: -sin2 x
C: -sinx
D: Tất cả sai
Quảng cáo
17 câu trả lời 134735
5 năm trước
Đáp án đúng là: B: -sin2x
Giải thích:
Để tính đạo hàm của hàm số y = cos2x, ta sử dụng công thức đạo hàm của hàm hợp và đạo hàm của hàm cos:
Đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) v'(x)
Đạo hàm của hàm cos: (cosx)' = -sinx
Áp dụng vào bài toán, ta có:
Đặt u = 2x => u' = 2
y' = (cos2x)' = -sin(2x) (2x)' = -2sin2x
Vậy đạo hàm của hàm số y = cos2x là y' = -2sin2x.
Đáp án A, C và D đều sai vì:
A: 2cosx.sinx là công thức của sin2x, không phải đạo hàm của cos2x.
C: -sinx chỉ là đạo hàm của cosx, không đúng với hàm số cos2x.
D: Tất cả sai là đáp án sai vì đã có đáp án B là đúng.
Giải thích:
Để tính đạo hàm của hàm số y = cos2x, ta sử dụng công thức đạo hàm của hàm hợp và đạo hàm của hàm cos:
Đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) v'(x)
Đạo hàm của hàm cos: (cosx)' = -sinx
Áp dụng vào bài toán, ta có:
Đặt u = 2x => u' = 2
y' = (cos2x)' = -sin(2x) (2x)' = -2sin2x
Vậy đạo hàm của hàm số y = cos2x là y' = -2sin2x.
Đáp án A, C và D đều sai vì:
A: 2cosx.sinx là công thức của sin2x, không phải đạo hàm của cos2x.
C: -sinx chỉ là đạo hàm của cosx, không đúng với hàm số cos2x.
D: Tất cả sai là đáp án sai vì đã có đáp án B là đúng.
y’ = (cos2x)’ = 2 . cosx. (cosx)’ = 2cosx . (-sinx) = -sin2x.
vậy câu hỏi bạn đặt ra trả lời câu B NHA
2 tháng trước
`y’ = (cos2x)’ = 2 . cosx. (cosx)’ = 2cosx . (-sinx) = -sin2x. `
Gửi ạ
3 năm trước
Chọn B.
Áp dụng công thức với u = cos x.
y’ = (cos2x)’ = 2.cos(cosx)’ = 2cosx.(-sinx) = -sin2x.
Nguyễn Văn Quân
· 3 năm trước
Chọn B. Áp dụng công thức với u = cos x. y’ = (cos2x)’ = 2.cos(cosx)’ = 2cosx.(-sinx) = -sin2x.
2 năm trước
chọn câu b nha
áp dụng công thức với u = cos x.
y’ = (cos2x)’ = 2.cos(cosx)’ = 2cosx.(-sinx) = -sin2x.
2 năm trước
Đáp án đúng là B: -sin2x.
Công thức đạo hàm của hàm `cos(u(x)) là: -sin(u(x)).u'(x)`
Trong trường hợp này, `u(x) = 2x`
Do đó, `y' = -sin(2x) * (2x)' = -sin(2x) * 2 = -sin2x`
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
Thành viên hăng hái nhất trong tuần
-
✦
3440 điểm
-
I miss you
1865 điểm
-
`color{blue}text{HuyTùng`
680 điểm
-
phuongthao
630 điểm
-
Haruto 560 điểm
-
Уйен изгелек >.<
450 điểm
-
Giaumy
450 điểm
-
ryn.lee
300 điểm
-
jgdmaX
265 điểm
-
$\Huge\color{white}{\text{.}}$
175 điểm
-
Kiều Anh 155 điểm
-
pie.thd_ 145 điểm
-
Ý Nguyễn Võ Như
145 điểm
-
Nguyễn Hoàng Bảo Nam
140 điểm
-
(๑﹏๑//)☪ảทջՇɦàทɦđêℳƙɦôทջℳưα
100 điểm
Rút gọn
Bài viết mới nhất Lớp 11
-
3 năm trước3525
-
3 năm trước3367
Gửi báo cáo thành công!
