
Ngọc
Kim cương đoàn
23,150
4630
Câu trả lời của bạn: 12:37 24/04/2025
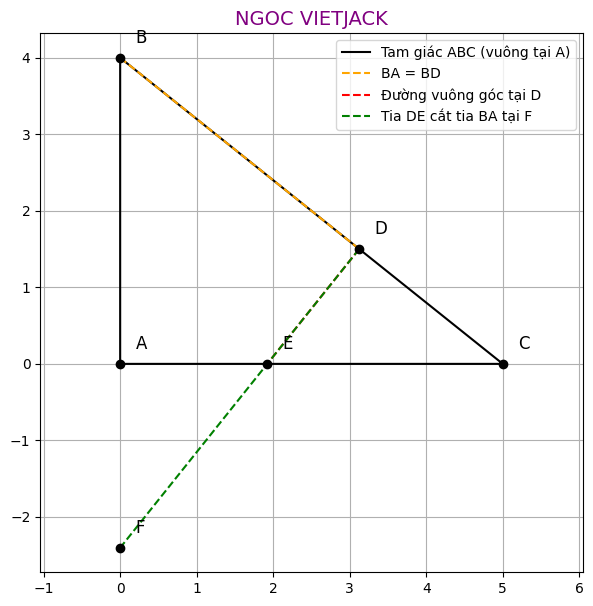
a) Chứng minh tam giác ABE = tam giác DBE:
Xét tam giác ABE và tam giác DBE, ta có:Góc BAE = 90 độ (vì tam giác ABC vuông tại A)
Góc BDE = 90 độ (vì DE vuông góc BC tại D)
Cạnh BE là cạnh chung.
BA = BD (theo giả thiết).
Do đó, tam giác ABE = tam giác DBE (theo trường hợp bằng nhau cạnh huyền - cạnh góc vuông).
b) Gọi F là giao điểm của DE và BA, chứng minh EF = EC:
Xét tam giác AFE và tam giác DCE, ta có:Góc FAE = Góc CDE = 90 độ.
AE = DE (vì tam giác ABE = tam giác DBE theo chứng minh ở câu a, đây là hai cạnh tương ứng).
Góc AEF = Góc DEC (hai góc đối đỉnh).
Do đó, tam giác AFE = tam giác DCE (theo trường hợp bằng nhau góc - cạnh - góc).
Suy ra EF = EC (hai cạnh tương ứng).
c) Chứng minh AD song song FC:
Cách 1: Sử dụng tính chất tam giác cân và góc đồng vị.
Vì BA = BD (giả thiết) nên tam giác ABD cân tại B.
Suy ra Góc BAD = Góc BDA.
Vì tam giác AFE = tam giác DCE (chứng minh ở câu b) nên AF = DC (hai cạnh tương ứng).
Ta có: BF = BA + AF và BC = BD + DC.
Mà BA = BD và AF = DC, suy ra BF = BC.
Do đó, tam giác BFC cân tại B.
Suy ra Góc BFC = Góc BCF.
Trong tam giác ABD cân tại B, Góc BDA = (180 độ - Góc ABC) / 2.
Trong tam giác BFC cân tại B, Góc BCF = (180 độ - Góc ABC) / 2.
Từ đó suy ra Góc BDA = Góc BCF.
Hai góc Góc BDA và Góc BCF đang ở vị trí đồng vị đối với hai đường thẳng AD và FC được cắt bởi đường thẳng BC.
Vậy AD song song với FC
Câu trả lời của bạn: 12:34 24/04/2025
Chia theo du dinh (ti le 5:6:7): Goi so goi tam du dinh chia cho lop 7A, 7B, 7C lan luot la a1, b1, c1. Ta co ti le: a1/5 = b1/6 = c1/7 = (a1 + b1 + c1) / (5 + 6 + 7) = T / 18 Suy ra:
a1 = (5 * T) / 18
b1 = (6 * T) / 18 = T / 3
c1 = (7 * T) / 18
Chia theo thuc te (ti le 4:5:6): Goi so goi tam thuc te chia cho lop 7A, 7B, 7C lan luot la a2, b2, c2. Ta co ti le: a2/4 = b2/5 = c2/6 = (a2 + b2 + c2) / (4 + 5 + 6) = T / 15 Suy ra:
a2 = (4 * T) / 15
b2 = (5 * T) / 15 = T / 3
c2 = (6 * T) / 15 = (2 * T) / 5
So sanh so goi tam nhan duoc: Ta so sanh so tam thuc te nhan duoc (a2, b2, c2) voi so tam du dinh (a1, b1, c1):
Lop 7A: a2 - a1 = (4T)/15 - (5T)/18 = (24T - 25T) / 90 = -T / 90 (Nhan it hon du dinh)
Lop 7B: b2 - b1 = T/3 - T/3 = 0 (Nhan bang du dinh)
Lop 7C: c2 - c1 = (2T)/5 - (7T)/18 = (36T - 35T) / 90 = T / 90 (Nhan nhieu hon du dinh)
Tim tong so goi tam (T): Theo de bai, co mot lop nhan nhieu hon du dinh 4 goi. Tu ket qua so sanh o tren, lop do chinh la lop 7C. Do do, ta co phuong trinh: c2 - c1 = 4 T / 90 = 4 T = 4 * 90 T = 360
Gia tri T = 360 thoa man dieu kien la so nguyen duong
Câu trả lời của bạn: 12:31 24/04/2025
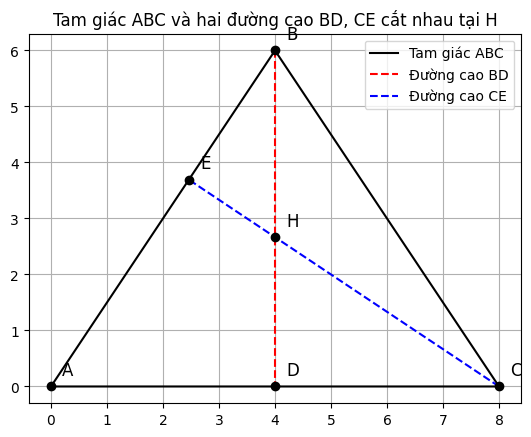
a) Cmr : tam giac ABD dong dang tam giac ACE
Xet tam giac ABD va tam giac ACE co:goc ADB = 90 do (vi BD la duong cao)
goc AEC = 90 do (vi CE la duong cao)
goc BAC la goc chung (hay goc BAD = goc CAE)
Do do, tam giac ABD dong dang voi tam giac ACE (goc-goc).
b) Cho AB=4cm; AC=5cm; AD=2cm. Tinh do dai doan thang AE
Vi tam giac ABD dong dang voi tam giac ACE (chung minh o cau a), ta co ti so cac canh tuong ung bang nhau: AB/AC = AD/AE = BD/CE
Thay cac gia tri da biet vao ti so AB/AC = AD/AE: 4/5 = 2/AE
Suy ra: AE = (5 * 2) / 4 = 10 / 4 = 2.5 cm
Vay, do dai doan thang AE la 2.5 cm.
c) Chung minh rang goc EDH = goc BCH
Xet tu giac BEDC:Ta co goc BEC = 90 do (vi CE la duong cao).
Ta co goc BDC = 90 do (vi BD la duong cao).
Hai dinh E va D cung nhin canh BC duoi mot goc 90 do.
Do do, tu giac BEDC la tu giac noi tiep (co the ve mot duong tron di qua ca 4 diem B, E, D, C, voi duong kinh la BC).
Vi BEDC la tu giac noi tiep, nen cac goc noi tiep cung chan mot cung thi bang nhau.
Xet cung BE cua duong tron ngoai tiep tu giac BEDC:Goc noi tiep BDE chan cung BE
Goc noi tiep BCE chan cung BE
Do do, goc BDE = goc BCE
Ma H la giao diem cua BD va CE, nen:H nam tren duong thang BD, do do goc BDE chinh la goc EDH
H nam tren duong thang CE, do do goc BCE chinh la goc BCH
=> goc EDH = goc BCH
Câu trả lời của bạn: 16:37 22/04/2025
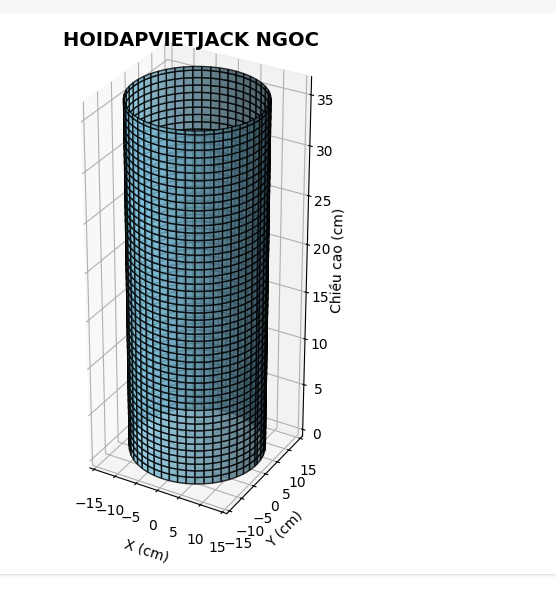
a) Tính thể tích của thùng nước
Bán kính đáy (r): Đường kính đáy là 28 cm, vậy bán kính đáy là:
r = 28 / 2 = 14 cm
Chiều cao (h): Chiều cao của thùng là 36 cm.
Thể tích hình trụ (V):
Công thức tính thể tích hình trụ là V = pi * r^2 * h.
Thay số vào công thức:
V = pi * (14^2) * 36 = pi * 196 * 36 = 7056 * pi (cm^3)
Tính giá trị
pi ≈ 3.14159, ta có:
V ≈ 7056 * 3.14159 ≈ 22167.077... cm^3
Làm tròn đến chữ số thập phân thứ nhất, ta được:
V ≈ 22167.1 cm^3
Tính số thùng nước cần đổ để đầy chum
Thể tích nước mỗi lần múc:
Do mỗi lần xách, lượng nước trong thùng chỉ còn 90%, nên thể tích nước thực tế mỗi lần múc là:
V_thuc_te = 90% * V = 0.9 * 7056 * pi ≈ 6350.4 * pi cm^3
V_thuc_te ≈ 0.9 * 22167.1 ≈ 19950.39 cm^3
Thể tích chum đựng nước:
Chum chứa được 0.5 m^3. Ta cần đổi đơn vị này sang cm^3 để tính toán:
1 m = 100 cm
1 m^3 = 100^3 = 1,000,000 cm^3
Vậy, thể tích chum là:
V_chum = 0.5 * 1,000,000 = 500,000 cm^3
= 500,000 / 19950.39
≈ 25.062...
Câu trả lời của bạn: 16:07 20/04/2025
a) Chứng minh: △AHB = △AHD
Xét △AHB và △AHD có:
∠AHB = ∠AHD = 90° (vì AH ⊥ BD)
Cạnh AH là cạnh chung
AB = AD (giả thiết)
Suy ra △AHB = △AHD (theo trường hợp cạnh huyền - cạnh góc vuông).
b) Chứng minh: EB = ED và AE là đường trung trực của đoạn BD
Chứng minh EB = ED:
Vì △AHB = △AHD (chứng minh ở câu a), ta có:HB = HD (hai cạnh tương ứng)
∠BAH = ∠DAH (hai góc tương ứng)
Xét △EHB và △EHD có:HB = HD (chứng minh trên)
∠EHB = ∠EHD = 90° (vì AH ⊥ BD, E thuộc AH)
Cạnh EH là cạnh chung
Suy ra △EHB = △EHD (theo trường hợp cạnh - góc - cạnh).
Do đó, EB = ED (hai cạnh tương ứng).
Chứng minh AE là đường trung trực của đoạn BD:
Ta có HB = HD (chứng minh trên), nên H là trung điểm của BD.
Ta có AH ⊥ BD tại H, mà E nằm trên tia AH, nên AE ⊥ BD.
Vì AE vuông góc với BD tại trung điểm H của BD, nên AE là đường trung trực của đoạn thẳng BD.
Cách khác chứng minh AE là trung trực:
Ta có AB = AD (giả thiết). Nên điểm A cách đều hai đầu mút B và D.
Ta có EB = ED (chứng minh trên). Nên điểm E cách đều hai đầu mút B và D.
Tập hợp các điểm cách đều hai đầu mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Vậy đường thẳng đi qua A và E chính là đường trung trực của đoạn thẳng BD.
c) Chứng minh: EC > EB
Trong △ABC, vì AB < AC (giả thiết), nên góc đối diện với cạnh AB nhỏ hơn góc đối diện với cạnh AC: ∠ACB < ∠ABC hay ∠C < ∠ABC.
Xét △ABE và △ADE có:AB = AD (giả thiết)
∠BAE = ∠DAE (vì ∠BAH = ∠DAH chứng minh ở câu b)
AE là cạnh chung
Suy ra △ABE = △ADE (cạnh - góc - cạnh).
Do đó, ∠ABE = ∠ADE (hai góc tương ứng).
Ta cần chứng minh EC > EB. Mà EB = ED (chứng minh ở câu b), vậy ta cần chứng minh EC > ED.
Xét △EDC. Để chứng minh EC > ED, ta cần chứng minh góc đối diện với EC lớn hơn góc đối diện với ED. Tức là ta cần chứng minh ∠EDC > ∠ECD (hay ∠EDC > ∠C).
Vì D nằm giữa A và C nên A, D, C thẳng hàng. Do đó, ∠ADE và ∠EDC là hai góc kề bù: ∠ADE + ∠EDC = 180°.
Suy ra ∠EDC = 180° - ∠ADE.
Mà ∠ADE = ∠ABE = ∠ABD (vì E nằm trên BC nên ∠ABE = ∠ABC không đúng, phải là ∠ABE = ∠ABD).
Vậy ∠EDC = 180° - ∠ABD.
Ta cần chứng minh 180° - ∠ABD > ∠C.
Điều này tương đương với 180° > ∠ABD + ∠C.
Xét △ABC có: ∠BAC + ∠ABC + ∠C = 180°. ∠BAC + (∠ABD + ∠EBC) + ∠C = 180°.
Do đó, 180° - (∠ABD + ∠C) = ∠BAC + ∠EBC.
Vậy, bất đẳng thức 180° > ∠ABD + ∠C tương đương với ∠BAC + ∠EBC > 0.
Vì △ABC là tam giác nhọn nên ∠BAC > 0.
Vì E là giao điểm của AH và BC, và H nằm giữa B và D, tia AH cắt BC tại E thì E nằm giữa B và C. Do đó ∠EBC > 0.
Vậy ∠BAC + ∠EBC > 0 là đúng.
Do đó, ∠EDC > ∠C là đúng.
Trong △EDC, vì ∠EDC > ∠C nên cạnh đối diện với ∠EDC lớn hơn cạnh đối diện với ∠C. Tức là EC > ED.
Mà ED = EB (chứng minh ở câu b).
Vậy EC > EB.
d) Chứng minh: Ba điểm D, E, F thẳng hàng
Xét △EBF và △EDC có:EB = ED (chứng minh ở câu b)
BF = DC (giả thiết)
Góc xen giữa:∠EBF: Vì F nằm trên tia đối của tia BA nên F, B, A thẳng hàng. Do đó ∠EBF và ∠EBA là hai góc kề bù. ∠EBF = 180° - ∠EBA. Mà E nằm trên BC, nên ∠EBA = ∠ABC? Không đúng. ∠EBA = ∠ABD. Vậy ∠EBF = 180° - ∠ABD.
∠EDC: Như đã chứng minh ở câu c, ∠EDC = 180° - ∠ADE. Mà ∠ADE = ∠ABE = ∠ABD (từ △ABE = △ADE). Vậy ∠EDC = 180° - ∠ABD.
Do đó, ∠EBF = ∠EDC.
Vậy △EBF = △EDC (theo trường hợp cạnh - góc - cạnh).
Suy ra ∠BEF = ∠DEC (hai góc tương ứng).
Ta có E là giao điểm của AH và BC, nên B, E, C thẳng hàng.
Do đó, ∠DEB + ∠DEC = 180° (hai góc kề bù).
Mà ∠DEC = ∠BEF (chứng minh trên).
Thay vào ta được: ∠DEB + ∠BEF = 180°.
Hai góc ∠DEB và ∠BEF là hai góc kề nhau có tổng bằng 180°, và có chung cạnh EB. Suy ra hai tia ED và EF là hai tia đối nhau.
Vậy ba điểm D, E, F thẳng hàng.
Kết luận: a) △AHB = △AHD (cạnh huyền - cạnh góc vuông) b) EB = ED và AE là đường trung trực của đoạn BD. c) EC > EB. d) Ba điểm D, E, F thẳng hàng.
Câu trả lời của bạn: 13:44 19/04/2025
Thời gian xuất phát: 6 giờ 15 phút
Vận tốc ban đầu (v1): 54 km/giờ
Kết luận (a): Lúc 8 giờ 45 phút, xe còn cách Thành phố Hồ Chí Minh 65 km.
b/
Câu trả lời của bạn: 18:28 18/04/2025
Gọi h là chiều cao của hình nón. Ta có mối liên hệ giữa bán kính đáy (r), chiều cao (h) và đường sinh (l) trong hình nón theo định lý Pytago: l^2 = h^2 + r^2
Từ đó suy ra: h^2 = l^2 - r^2 h = căn bậc hai của (l^2 - r^2)
Thay : r = 6 cm l = 10 cm
h^2 = 10^2 - 6^2 h^2 = 100 - 36 h^2 = 64 h = căn bậc hai của (64) h = 8 cm
Câu trả lời của bạn: 10:24 18/04/2025
a) Chứng minh △ACH=△ECH
b) Chứng minh HB=HC
c) Chứng minh AH<BH và BH−AH<AC
Chứng minh AH<BH:
Chứng minh BH−AH<AC:
Câu trả lời của bạn: 10:21 18/04/2025
Quãng đường mỗi xe đi được:
Xe máy đi từ A đến C: 80 km.
Ô tô đi từ B đến C: 180 km - 80 km = 100 km.
Thời gian hai xe đi:
Hai xe khởi hành cùng lúc và gặp nhau tại C, nên thời gian đi của hai xe là như nhau.
Gọi thời gian đó là t (giờ).
Vận tốc mỗi xe:
Ta biết: Vo = Vm + 10 (ô tô nhanh hơn xe máy 10 km/h).
Liên hệ quãng đường, vận tốc, thời gian:
Xe máy: Quãng đường = Vận tốc * Thời gian => 80 = Vm * t
Ô tô: Quãng đường = Vận tốc * Thời gian => 100 = Vo * t
Tìm tỉ lệ vận tốc:
Từ hai công thức trên, ta lấy cái dưới chia cho cái trên: 100 / 80 = (Vo * t) / (Vm * t) 100 / 80 = Vo / Vm 5 / 4 = Vo / Vm
Nghĩa là: 5 * Vm = 4 * Vo
Giải
Ta có hai thông tin:Vo = Vm + 10
5 * Vm = 4 * Vo
Thay Vo từ thông tin thứ nhất vào thông tin thứ hai: 5 * Vm = 4 * (Vm + 10) 5 * Vm = 4 * Vm + 40 5 * Vm - 4 * Vm = 40 1 * Vm = 40 Vậy, vận tốc xe máy Vm = 40 km/h
Tìm vận tốc ô tô: Vo = Vm + 10 = 40 + 10 = 50 km/h
Câu trả lời của bạn: 10:19 18/04/2025
Bài thơ "Thuốc đắng" của Mai Văn Phấn chứa đựng những nét đặc sắc nghệ thuật đáng chú ý. Trước hết, bài thơ sử dụng thể thơ tự do với những câu thơ dài ngắn linh hoạt, phù hợp với việc diễn tả dòng cảm xúc, suy tư miên man, đầy trăn trở của người cha. Ngôn ngữ thơ giản dị, mộc mạc nhưng giàu sức gợi ("cơn sốt thiêu con", "mồ hôi keo thành chai tay"). Đặc biệt, tác giả đã xây dựng thành công những hình ảnh thơ giàu ý nghĩa biểu tượng. Hình ảnh trung tâm "chén thuốc đắng" vừa mang nghĩa tả thực về chén thuốc cho con, vừa là ẩn dụ cho những cay đắng, nhọc nhằn, vất vả mà người cha đã và đang trải qua trong cuộc đời. Những hình ảnh đối lập như "cánh hoa mỏng manh" và "rễ cay", hay sự kết hợp bất ngờ "Mùa xuân tràn vào chén đắng" tạo nên những liên tưởng sâu sắc về mối quan hệ giữa khó khăn và thành quả, giữa hiện tại và tương lai, giữa nỗi buồn và niềm hy vọng. Giọng điệu thơ trầm lắng, ngậm ngùi, thấm đẫm tình phụ tử thiêng liêng và những chiêm nghiệm về cuộc sống. Tất cả hòa quyện tạo nên một bài thơ giản dị mà lắng đọng, giàu dư vị
Câu trả lời của bạn: 10:15 18/04/2025
Xác định vị trí A, B so với đường thẳng d (x+2y+6=0):
Thay điểm A(-1; -3) vào d: (-1) + 2*(-3) + 6 = -1 - 6 + 6 = -1 (nhỏ hơn 0)
Thay điểm B(7; 5) vào d: 7 + 2*(5) + 6 = 7 + 10 + 6 = 23 (lớn hơn 0)
Vì kết quả trái dấu (-1 và 23) nên A và B nằm khác phía so với đường thẳng d.
Tìm điểm M để (3MA + MB) nhỏ nhất:
Mẹo: Khi A và B nằm khác phía so với đường thẳng d, giá trị k⋅MA+MB (với k>0) thường đạt giá trị nhỏ nhất tại giao điểm của đoạn thẳng AB với đường thẳng d. (Điều này đúng cho cả MA+MB và cả 3MA+MB trong trường hợp này).
Vậy, ta cần tìm giao điểm của đường thẳng AB và đường thẳng d.
Viết phương trình đường thẳng AB:
Đi qua A(-1; -3) và B(7; 5).
Vector chỉ phương AB = (7 - (-1), 5 - (-3)) = (8, 8). Chọn vector đơn giản hơn là (1, 1).
Vector pháp tuyến là (1, -1).
Phương trình AB: 1*(x - (-1)) - 1*(y - (-3)) = 0 x + 1 - (y + 3) = 0 x - y - 2 = 0
Tìm giao điểm M của AB và d:
Ta giải hệ phương trình:d: x + 2y + 6 = 0
AB: x - y - 2 = 0
Từ AB => x = y + 2. Thay vào d: (y + 2) + 2y + 6 = 0 3y + 8 = 0 y = -8/3
Thay y = -8/3 vào x = y + 2: x = -8/3 + 2 = -8/3 + 6/3 = -2/3
Vậy điểm M là (-2/3; -8/3).
Tính a + b:
Điểm M có tọa độ (a; b) nên a = -2/3 và b = -8/3.
a + b = (-2/3) + (-8/3) = -10/3
Câu trả lời của bạn: 10:12 18/04/2025
Tính "đà" (động lượng) lúc đầu:
Vật 1: nặng 2kg, chạy 4m/s => Đà = 2 * 4 = 8 (theo hướng ban đầu)
Vật 2: nặng 3kg, đứng yên => Đà = 3 * 0 = 0
Tổng "đà" lúc đầu = 8 + 0 = 8
Tính "đà" lúc sau:
Vật 2: nặng 3kg, chạy 60m/s (cùng hướng vật 1 ban đầu) => Đà = 3 * 60 = 180
Vật 1: chưa biết chạy thế nào, gọi "đà" của nó là Đà_1_mới.
Tổng "đà" lúc sau = Đà_1_mới + 180
"Đà" lúc đầu phải bằng "đà" lúc sau:
8 = Đà_1_mới + 180
Tìm "đà" của vật 1 lúc sau:
Đà_1_mới = 8 - 180 = -172
Tìm vận tốc vật 1 lúc sau:
Vận tốc vật 1 mới = -172 / 2 = -86 m/s
Câu trả lời của bạn: 10:11 18/04/2025
Phần diện tích tăng thêm (không tính góc 9x7): 7 * dài + 9 * rộng = 963 - (9 * 7) = 900 (m²).
Giải hệ từ (1) và (2): Tìm được Rộng = 30m, Dài = 90m
Câu trả lời của bạn: 19:23 16/04/2025
điều kiện để phương trình có 2 nghiệm phân biệt:
Phương trình là: xx - 2(m-3)x + (mm - 8*m + 5) = 0
Để có 2 nghiệm phân biệt, delta phẩy phải lớn hơn 0. Ta tính delta phẩy: Delta phẩy = [-(m-3)][-(m-3)] - 1(mm - 8m + 5) = (3-m)(3-m) - (mm - 8m + 5) = (9 - 6m + mm) - (mm - 8m + 5) = 9 - 6m + mm - mm + 8m - 5 = 2m + 4
Điều kiện delta phẩy > 0 tương đương với: 2m + 4 > 0 2m > -4 m > -2
Vậy, điều kiện là m > -2
Dùng vitet
Khi m > -2, phương trình có 2 nghiệm phân biệt x1, x2. Theo Vi-ét:
Điều kiện là: x1x1 + 2x2x2 - 3x1*x2 = x1 - x2
= (x1 - x2) * (x1 - 2*x2)
(x1 - x2) * (x1 - 2*x2) = (x1 - x2)
(x1 - 2*x2) = 1
(b) x1 - 2x2 = 1
=> x2 = (2*m - 7) / 3
x1 = (4*m - 11) / 3
8mm - 50m + 77 = 9mm - 72m + 45
0 = mm - 22m - 32
giải pt tìm m
= 484 + 128 = 612
Căn(612) = Căn(36 * 17) = 6 * Căn(17) (Ghi chú: Căn(17) là căn bậc hai của 17)
m = 11 cộng hoặc trừ 3 * Căn(17)
m2 = 11 - 3 * Căn(17)
m2 = 11 - 3 * Căn(17): Ta biết Căn(16)=4 và Căn(25)=5, nên Căn(17) nằm giữa 4 và 5. Vậy 3 * Căn(17) sẽ nằm giữa 34=12 và 35=15. Do đó, 11 - 3 * Căn(17) sẽ nằm giữa (11 - 15) = -4 và (11 - 12) = -1. Giá trị này nằm trong khoảng (-4, -1), nên nó lớn hơn -2. (Thỏa mãn)
Câu trả lời của bạn: 19:16 16/04/2025
a) Chứng minh tam giác AHB = tam giác AHC
Xét hai tam giác vuông AHB và AHC có:∠AHB = ∠AHC = 90° (vì AH là đường cao)
AB = AC (vì tam giác ABC cân tại A)
AH là cạnh chung
Vậy tam giác AHB = tam giác AHC (theo trường hợp cạnh huyền - cạnh góc vuông).
b) Từ H kẻ đường thẳng song song với AC cắt AB tại D. Chứng minh AD = DH
Vì tam giác AHB = tam giác AHC (chứng minh ở câu a), suy ra:∠BAH = ∠CAH (hai góc tương ứng). Hay ∠DAH = ∠CAH.
Vì HD // AC (giả thiết), suy ra:∠DHA = ∠CAH (hai góc so le trong).
Từ hai điều trên, ta có ∠DAH = ∠DHA (= ∠CAH).
Xét tam giác ADH có ∠DAH = ∠DHA, suy ra tam giác ADH cân tại D.
Vậy AD = DH (hai cạnh bên của tam giác cân).
c) Gọi E là trung điểm AC, CD cắt AH tại G. Chứng minh B, G, E thẳng hàng
Xét tam giác ABC có:AH là đường cao (giả thiết).
Vì tam giác ABC cân tại A, đường cao AH cũng đồng thời là đường trung tuyến. Do đó, H là trung điểm của BC.
Xét tam giác ABC:H là trung điểm BC (chứng minh trên).
HD // AC (giả thiết).
Theo định lý về đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì nó đi qua trung điểm cạnh thứ ba. Suy ra D là trung điểm của AB.
Xét tam giác ABC có:AH là đường trung tuyến (ứng với cạnh BC).
CD là đường trung tuyến (vì D là trung điểm AB).
G là giao điểm của AH và CD (giả thiết).
Do đó, G là trọng tâm của tam giác ABC.
Lại có E là trung điểm của AC (giả thiết), suy ra BE cũng là đường trung tuyến của tam giác ABC (ứng với cạnh AC).
Theo tính chất trọng tâm của tam giác, ba đường trung tuyến đồng quy tại trọng tâm. Vì G là trọng tâm nên G phải thuộc đường trung tuyến BE.
Vậy ba điểm B, G, E cùng nằm trên đường trung tuyến BE, hay B, G, E thẳng hàng.
Câu trả lời của bạn: 16:59 15/04/2025
sai đề
Câu trả lời của bạn: 19:46 14/04/2025
Trường hợp xấu nhất là e bốc phải tất cả các viên bi không phải màu đỏ trước khi bốc được viên bi đỏ thứ 7.
e bốc hết số bi xanh: 10 viên.
e bốc hết số bi vàng: 19 viên.
Tổng số bi không phải màu đỏ bạn đã bốc là: 10 + 19 = 29 viên.
Lúc này, trong hộp chỉ còn lại bi màu đỏ. Để chắc chắn có được 7 viên bi màu đỏ, bạn cần bốc thêm 7 viên nữa.
Vậy, tổng số viên bi cần bốc ra ít nhất để chắc chắn có được 7 viên bi màu đỏ là: 10 (bi xanh) + 19 (bi vàng) + 7 (bi đỏ) = 36 viên bi.
Giải thích: Bằng cách lấy ra 36 viên bi e đảm bảo rằng ngay cả trong trường hợp không may mắn nhất (lấy hết bi xanh và bi vàng trước), e vẫn sẽ có đủ 7 viên bi đỏ.
Câu trả lời của bạn: 13:59 14/04/2025
Cho tam giác ABC vuông tại A, có đường cao AH. Biết BH = 3 cm và CH = 4 cm.
độ dài đường cao AH: Trong tam giác vuông ABC, đường cao AH ứng với cạnh huyền BC. Ta có hệ thức lượng trong tam giác vuông: AH² = BH * CH AH² = 3 cm * 4 cm = 12 cm² AH = √12 cm = 2√3 cm
tan B: Xét tam giác vuông AHB (vuông tại H): tan B = Đối / Kề = AH / BH tan B = (2√3 cm) / (3 cm) = 2√3 / 3
h cot C: Xét tam giác vuông AHC (vuông tại H): cot C = Kề / Đối = CH / AH cot C = (4 cm) / (2√3 cm) = 4 / (2√3) = 2 / √3 = (2 * √3) / (√3 * √3) = 2√3 / 3
giá trị biểu thức Q: Q = tan B + cot C Q = (2√3 / 3) + (2√3 / 3) Q = (2√3 + 2√3) / 3 Q = 4√3 / 3
Câu trả lời của bạn: 13:56 14/04/2025
Hình ảnh thờ Trà Kiệu – một kiệt tác điêu khắc Chăm-pa thế kỷ X – gợi cho em nhiều suy nghĩ sâu sắc về trình độ kỹ thuật và đời sống văn hóa phong phú của cư dân Chăm-pa xưa.
Trước hết, về trình độ kỹ thuật, tác phẩm cho thấy cư dân Chăm-pa đã đạt đến trình độ điêu luyện trong nghệ thuật chạm khắc trên đá. Các chi tiết hoa văn, hình thể con người, thần linh được thể hiện một cách tinh xảo, sinh động, có chiều sâu. Độ tỉ mỉ, khả năng phối hợp hài hòa giữa các yếu tố hình khối và đường nét cho thấy người Chăm đã nắm vững kỹ thuật tạc đá và có tư duy thẩm mỹ rất cao.
Về đời sống văn hóa, tác phẩm phản ánh một xã hội đậm đà bản sắc tôn giáo – tín ngưỡng, cụ thể là ảnh hưởng mạnh mẽ của Ấn Độ giáo và Phật giáo. Những hình ảnh các vị thần linh, vũ nữ, lễ nghi thể hiện đời sống tinh thần phong phú, nơi nghệ thuật gắn liền với đức tin, lễ nghi và triết lý sống. Điều này chứng tỏ cư dân Chăm không chỉ sống dựa vào thiên nhiên mà còn có đời sống tinh thần phát triển rực rỡ, có tổ chức xã hội và tư tưởng sâu sắc.
vậy thờ Trà Kiệu là minh chứng sống động cho một nền văn minh Chăm-pa phát triển rực rỡ, nơi nghệ thuật và đời sống tinh thần hòa quyện tạo nên những giá trị văn hóa độc đáo và trường tồn
Câu trả lời của bạn: 13:53 14/04/2025
Chứng minh:
a) GA = GD
Vì AM là đường trung tuyến của ΔABC và G là trọng tâm (giao điểm của hai đường trung tuyến AM và BN), theo tính chất trọng tâm, ta có:AG = (2/3)AM
GM = (1/3)AM
Do đó, AG = 2 * GM.
Theo giả thiết, D nằm trên tia đối của tia MG và MD = MG.
Xét đoạn thẳng GD: GD = GM + MD.
Vì MD = MG, nên GD = MG + MG = 2 * MG.
Từ AG = 2 * GM và GD = 2 * GM, suy ra GA = GD (điều phải chứng minh).
b) ∆MBG = ∆MCD
Xét hai tam giác MBG và MCD, ta có:MB = MC (Vì AM là đường trung tuyến nên M là trung điểm của BC).
∠BMG = ∠CMD (Hai góc đối đỉnh).
MG = MD (Theo giả thiết).
Vậy, ∆MBG = ∆MCD (c.g.c - cạnh, góc, cạnh) (điều phải chứng minh).
c) CD = 2GN
Vì ∆MBG = ∆MCD (chứng minh ở câu b), suy ra cạnh tương ứng bằng nhau:BG = CD (1)
Vì BN là đường trung tuyến của ΔABC và G là trọng tâm, theo tính chất trọng tâm, ta có:BG = (2/3)BN
GN = (1/3)BN
Do đó, BG = 2 * GN (2)
Từ (1) và (2), suy ra CD = 2GN (điều phải chứng minh).


