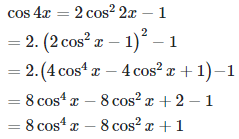Quảng cáo
3 câu trả lời 84374
cos4x=2cos22x-1=2.(2cos2x-1)2-1=2.(4cos4x-4cos2x+1)-1=8cos4x-8cos2x+2-1=8cos4x-8cos2x+1.
1. Công thức biểu diễn cos4x\cos 4xcos4x
Từ công thức nhân đôi của cos:
cos2θ=2cos2θ−1\cos 2\theta = 2\cos^2 \theta - 1cos2θ=2cos2θ−1Áp dụng công thức trên cho 2x2x2x, ta có:
cos4x=2cos22x−1\cos 4x = 2\cos^2 2x - 1cos4x=2cos22x−1Tiếp tục thay cos2x=2cos2x−1\cos 2x = 2\cos^2 x - 1cos2x=2cos2x−1, ta có:
cos4x=2(2cos2x−1)2−1\cos 4x = 2(2\cos^2 x - 1)^2 - 1cos4x=2(2cos2x−1)2−12. Biến đổi chi tiết
=2(4cos4x−4cos2x+1)−1= 2(4\cos^4 x - 4\cos^2 x + 1) - 1=2(4cos4x−4cos2x+1)−1 =8cos4x−8cos2x+2−1= 8\cos^4 x - 8\cos^2 x + 2 - 1=8cos4x−8cos2x+2−1 =8cos4x−8cos2x+1= 8\cos^4 x - 8\cos^2 x + 1=8cos4x−8cos2x+13. Kết quả cuối cùng
cos4x=8cos4x−8cos2x+1\cos 4x = 8\cos^4 x - 8\cos^2 x + 1cos4x=8cos4x−8cos2x+1
Quảng cáo
Câu hỏi hot cùng chủ đề
Xếp hạng tuần này
Xếp hạng tháng này
草原 (Phone 🐼)1710 điểm
Bertha🐼1160 điểm
I love Sang in BD880 điểm
vrss750 điểm
Duy Anh695 điểm
Đứchsganh^0^480 điểm
chu dang hihi430 điểm
Tongtai depzai 🐼395 điểm
Khả Di (phone🐼)355 điểm
vegeta ultra ego350 điểmCông Thắng Bùi210 điểm
G195 điểm
ɱʏ WĄîfu130 điểm
Angel Tanysha120 điểm
Lily (타오린)115 điểm
Bài viết mới nhất Lớp 11
-
3 năm trước3031
-
3 năm trước2986
