Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực
Lời giải Bài 9.20 trang 58 SBT Toán 7 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 9.20 trang 58 SBT Toán 7 Tập 2: Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S. Chứng minh tia PO là tia phân giác của góc RPS.
Lời giải:
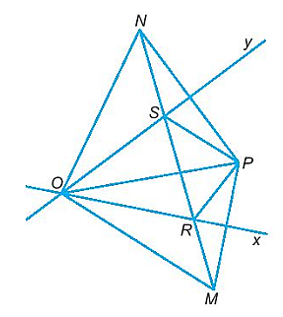
Tam giác OPM là tam giác cân tại O (vì Ox là đường trung trực của đoạn thẳng PM).
Suy ra (1) và OM = OP.
Lại có tam giác RPM là tam giác cân tại R (vì Ox, hay chính là Rx là đường trung trực của đoạn thẳng PM).
Suy ra (2)
Trừ vế với vế của (1) cho (2) ta có: .
Hay (*)
Tương tự ta có tam giác OPN là tam giác cân tại O (vì Oy là đường trung trực của đoạn thẳng PN).
Suy ra (3) và ON = OP.
Lại có tam giác SPN là tam giác cân tại R (vì Oy, hay chính là Sy là đường trung trực của đoạn thẳng PN).
Suy ra (4)
Trừ vế với vế của (3) cho (4) ta có: .
Hay (**)
Vì OM = ON (= OP) nên tam giác OMN là tam giác cân tại O.
Do đó: (***)
Từ (*), (**), (***) ta suy ra .
Vậy suy ra PO là tia phân giác của góc RPS (đpcm).
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:
Bài 9.19 trang 58 SBT Toán 7 Tập 2: Cho tam giác ABC vuông. Kẻ đường thẳng vuông góc với cạnh huyền BC của tam giác ABC tại điểm D không thuộc đoạn BC. Nó cắt đường thẳng chứa cạnh AB tại E và cắt đường thẳng chứa cạnh AC tại F. Xác định trực tâm của tam giác BEF...
Bài 9.20 trang 58 SBT Toán 7 Tập 2: Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S. Chứng minh tia PO là tia phân giác của góc RPS...
Bài 9.21 trang 58 SBT Toán 7 Tập 2: Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh ...
Bài 9.22 trang 58 SBT Toán 7 Tập 2: a) Giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điểm D nằm giữa A và C. Chứng minh AC > AB...
Bài viết liên quan
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 32: Quan hệ giữa đường vuông góc và đường xiên
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 33: Quan hệ giữa ba cạnh trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
- Giải Sách bài tập Toán 7 Kết nối tri thức Ôn tập chương 9
