Giải sách bài tập Toán lớp 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

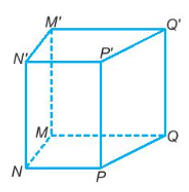
Bài 10.9 trang 65 SBT Toán 7 Tập 2: Gọi tên đỉnh, cạnh đáy, cạnh bên, mặt đáy, mặt bên của hình lăng trụ đứng tứ giác MNPQ.M’N’P’Q’ trong Hình 10.7.

Lời giải:

Quan sát Hình 10.7, hình lăng trụ đứng tứ giác MNPQ.M’N’P’Q’ có:

- Các đỉnh: M, N, P, Q, M’, N’, P’, Q’;

- Các cạnh đáy: MN, NP, PQ, QM, M’N’, N’P’, P’Q’, Q’M’;

- Các cạnh bên: MM’, NN’, PP’, QQ’;

- Các mặt đáy: MNPQ, M’N’P’Q’;

- Các mặt bên: M’N’NM, N’P’PN, P’Q’QP, Q’M’MQ.

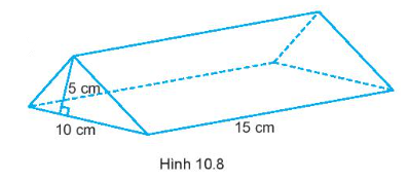
Bài 10.10 trang 66 SBT Toán 7 Tập 2: Tính thể tích hình lăng trụ đứng tam giác trong Hình 10.8.

Lời giải:

Mặt đáy của hình lăng trụ là tam giác có đường cao là 5 cm và cạnh đáy là 10 cm.

Diện tích đáy của hình lăng trụ là: $S=\frac{1}{2}.10.5=25\left(c{m}^2\right)$

Thể tích của hình lăng trụ đứng có đường cao là 15 cm là:

V = S . h = 25 . 15 = 375 (cm³).

Vậy thể tích của hình lăng trụ đứng có đường cao là 15 cm là 375 cm³.

Bài 10.11 trang 66 SBT Toán 7 Tập 2: Một hình lăng trụ đứng đáy là một tứ giác có chu vi 30 cm, chiều cao của hình lăng trụ là 8 cm. Tính diện tích xung quanh của hình lăng trụ đó.

Lời giải:

Một hình lăng trụ đứng có đáy là một tứ giác có chu vi 30 cm, chiều cao của hình lăng trụ là 8 cm.

Diện tích xung quanh của hình lăng trụ là:

S_xq = C . h = 30 . 8 = 240 (cm²)

Vậy diện tích xung quanh của hình lăng trụ là 240 cm².

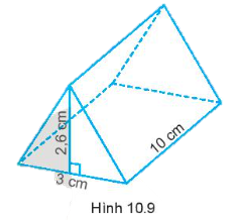
Bài 10.12 trang 66 SBT Toán 7 Tập 2: Một lăng kính thủy tinh có dạng hình lăng trụ đứng có đáy là tam giác đều, kích thước như Hình 10.9.

a) Tính thể tích của lăng kính thủy tinh.

b) Người ta làm một chiếc hộp bằng bìa cứng để đựng vừa khít lăng kính thủy tinh nói trên (hở hai đáy tam giác). Tính diện tích bìa cần dùng (bỏ qua mép nối).

Lời giải:

a) Lăng kính thủy tinh dạng hình lăng trụ đứng có đáy là một tam giác có đường cao là 2,6 và cạnh đáy là 3 cm.

Diện tích đáy của lăng kính là: $S=\frac{1}{2}.3.2,6=3,9\left(c{m}^2\right)$

Thể tích lăng kính thủy tinh có đường cao là 10 cm là:

V = S . h = 3,9 . 10 = 39 (cm³)

b) Chu vi đáy tam giác đều của lăng kính thủy tinh là:

3 . 3 = 9 (cm)

Diện tích bìa cứng cần dùng chính là diện tích xung quanh của lăng kính thủy tinh và bằng:

S_xq = 9 . 10 = 90 (cm²)

Vậy diện tích bìa cần dùng 90 cm².

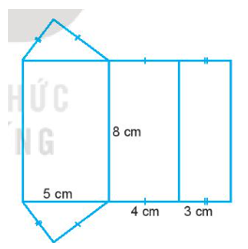
Bài 10.13 trang 66 SBT Toán 7 Tập 2: Một hình lăng trụ đứng có hình khai triển như Hình 10.10. Tính diện tích xung quanh của hình lăng trụ.

Lời giải:

Sau khi gấp miếng bìa trên, sẽ tạo thành một hình lăng trụ đứng có dạng như sau:

Chu vi mặt đáy của hình lăng trụ đứng là:

C = 3 + 4 + 5 = 12 (cm)

Diện tích xung quanh của hình lăng trụ là:

S_xq = C . h = 12 . 8 = 96 (cm²).

Vậy diện tích xung quanh của hình lăng trụ là 96 cm².

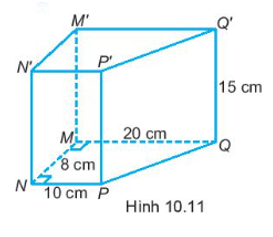
Bài 10.14 trang 66 SBT Toán 7 Tập 2: Cho hình lăng trụ đứng MNPQ.M’N’P’Q’ có đáy MNPQ là hình thang vuông tại M và N. Kích thước các cạnh như trong Hình 10.11. Tính thể tích hình lăng trụ.

Lời giải:

Diện tích mặt đáy có dạng hình thang vuông MNPQ là: $S=\frac{1}{2}\left(MQ+NP\right).MN$$=\frac{1}{2}\left(20+10\right).8=120\left(c{m}^2\right)$

Thể tích của hình lăng trụ đứng MNPQ.M’N’P’Q’ là:

V = S . h = 120 . 15 = 1 800 (cm³).

Vậy thể tích hình lăng trụ 1 800 cm³.

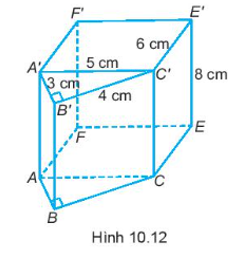
Bài 10.15 trang 67 SBT Toán 7 Tập 2: Một hình lăng trụ đứng được ghép bởi một hình lăng trụ đứng tam giác và một hình hộp chữ nhật có kích thước như trong Hình 10.12. Tính thể tích của hình lăng trụ đứng ABCEF.A’B’C’E’F’.

Lời giải:

Diện tích mặt đáy có dạng hình tam giác vuông ABC của lăng trụ đứng A’B’C’.ABC là: $S_1=\frac{1}{2}.AB.BC=\frac{1}{2}.3.4=6\left(c{m}^2\right)$

Khi đó, thể tích của hình lăng trụ đứng A’B’C’.ABC là:

V₁ = S₁ . h = 6 . 8 = 48 (cm³)

Diện tích mặt đáy có dạng hình chữ nhật ACEF của lăng trụ đứng A’C’E’F’.ACEF là:

S₂ = AC . EC = 5 . 6 = 30 (cm²)

Thể tích của hình lăng trụ đứng A’C’E’F’.ACEF là:

V₂ = S₂ . h = 30 . 8 = 240 (cm³)

Thể tích của hình lăng trụ đứng ABCEF.A’B’C’E’F’ là:

V = V₁ + V₂ = 48 + 240 = 288 (cm³)

Vậy thể tích của hình lăng trụ đứng ABCEF.A’B’C’E’F’ là 288 cm³.