Giải sách bài tập Toán lớp 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Bài 9.14 trang 55 SBT Toán 7 Tập 2: Cho góc xAy và một điểm G trong góc đó. Lấy hai điểm M, N trên tia AG sao cho . Qua N kẻ đường thẳng song song với đường thẳng chứa tia Ax, nó cắt Ay tại C. Đường thẳng CM cắt Ax tại B.

a) Chứng minh hai tam giác ABM và NCM bằng nhau, từ đó suy ra AM là đường trung tuyến của tam giác ABC.

b) Chứng minh rằng G là trọng tâm của tam giác ABC vừa dựng được.

Lời giải:

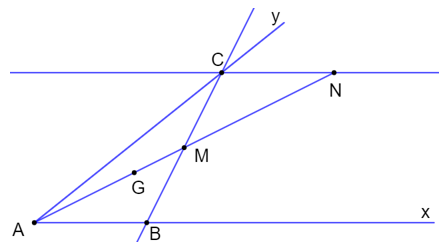
a) Ta có: CN // Ax hay CN // AB

Suy ra $\widehat{BAM}=\widehat{CNM}$  (Hai góc so le trong)

Lại có: AN = 2AM nên suy ra AM = NM

Xét hai tam giác ABM và NCM có:

$\widehat{BAM}=\widehat{CNM}$ (cmt)

AM = NM (cmt)

$\widehat{AMB}=\widehat{NMC}$ (Hai góc đối bằng nhau)

Suy ra ∆ ABM = ∆ NCM (g.c.g)

b) Ta có: ∆ ABM = ∆ NCM (cmt)

Nên suy ra BM = CM (Hai cạnh tương ứng bằng nhau)

Xét tam giác ABC có BM = CM nên M là trung điểm của BC.

Nên suy ra AM là đường trung tuyến.

Vì G là điểm thuộc AM có $AM=\frac{3}{2}AG$ .

Hay $AG=\frac{2}{3}AM$ .

Do đó G là trọng tâm của tam giác ABC (đpcm).

Bài 9.15 trang 55 SBT Toán 7 Tập 2: Gọi M là trung điểm của cạnh BC của tam giác ABC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm của AB cắt BC tại U, đường thẳng qua D và trung điểm của AC cắt BC tại V. Chứng minh BU = UV = VC.

Lời giải:

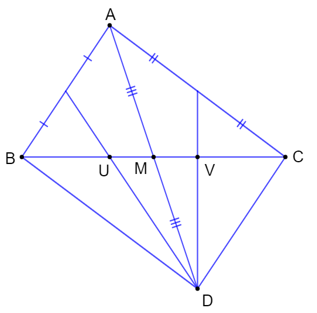
+) Tam giác BAC có M là trung điểm của BC nên suy ra MB = MC (1)

+) Xét tam giác ABD có U là giao của 2 đường trung tuyến BM và DE nên U là trọng tâm tam giác ABD

Vậy áp dụng định lí 1 ta có:  $\frac{BU}{MB}=\frac{2}{3}$

Suy ra $BU=\frac{2}{3}MB$  (2)

Từ đó ta có: $UM=BM-BU=MB-\frac{2}{3}MB=\frac{1}{3}MB$  (3)

+) Xét tam giác ACD có V là giao của 2 đường trung tuyến CM và DF nên V là trọng tâm tam giác AVD

Vậy áp dụng định lí 1 ta có:  $\frac{VC}{MC}=\frac{2}{3}$

Suy ra $VC=\frac{2}{3}MC$  (4)

Từ đó ta có: $MV=CM-VC$ $=MC-\frac{2}{3}MC=\frac{1}{3}MC$  (5)

Từ (1), (3), (5) ta có:

$UV=UM+MV$$=\frac{1}{3}MB+\frac{1}{3}MC=\frac{2}{3}MB$ (6)

Từ (1), (2), (4), (6) ta có: $BU=UV=VC=\frac{2}{3}MB$  (đpcm).

Bài 9.16 trang 55 SBT Toán 7 Tập 2:

a) Gọi I là giao điểm của hai đường phân giác BE và CF của tam giác ABC. Đường thẳng qua I song song với BC cắt AB tại J và cắt AC tại K. Chứng minh JK = BJ + CK.

b) Đường thẳng qua B vuông góc với BI cắt đường thẳng qua C vuông góc với CI tại điểm I’. Qua I’ kẻ đường thẳng song song với BC cắt AB tại J’, cắt AC tại K’. Chứng minh J’K’ = BJ’ + CK’.

Lời giải:

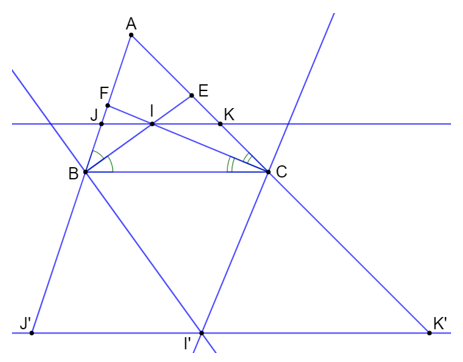
a) Xét tam giác BFC có BI là đường phân giác nên ta có:

$\widehat{FBI}=\widehat{IBC}$ hay $\widehat{JBI}=\widehat{IBC}$  (5)

Lại có do JI // BC nên ta suy ra được: $\widehat{JIB}=\widehat{IBC}$  (hai góc so le trong)

Vậy suy ra . Từ đó ta suy tam tam giác JIB cân tại J.

Suy ra JI = BJ (1)

Tương tự ta chứng minh được tam giác KIC cân tại I.

Suy ra KI = CK (2)

Từ (1) và (2) suy ra: JK = JI + IK = BJ + CK (đpcm).

b) Vì BI’ vuông góc với BI nên $\widehat{I\text{'}BC}+\widehat{CBI}=90°$  (3)

Và $\widehat{JBI}+\widehat{I\text{'}BJ\text{'}}=180°-\left(\widehat{I\text{'}BC}+\widehat{CBI}\right)$$=180°-90°=90°$  (4)

Từ (3), (4) và (5) suy ra $\widehat{CBI}=\widehat{I\text{'}BJ\text{'}}$ .

Vậy suy ra BI’ là tia phân giác của góc tạo bởi BC và BJ’.

Chứng minh tương tự ta suy ra CI’ là tia phân giác của góc tạo bởi CB và CK’.

Chứng minh tương tự câu a) ta dễ dàng suy ra được tam giác J’BI’ cân tại J’ và tam giác K’CI’ cân tại K’.

Vậy suy ra J’B = J’I’ và K’C = K’I’.

Vậy ta có: J’K’ = J’I’ + I’K’ = J’B + K’C (đpcm).

Bài 9.17 trang 55 SBT Toán 7 Tập 2: Tam giác ABC có AD, BE là hai đường phân giác và . Chứng minh rằng DE là tia phân giác của góc ADC.

Lời giải:

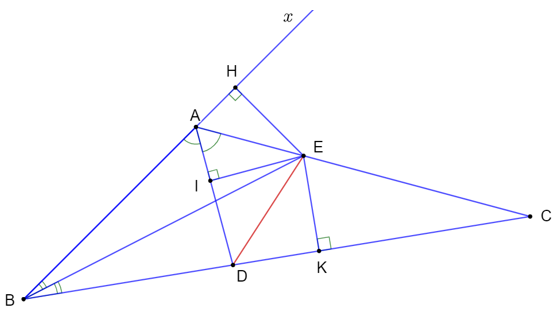
Gọi Ax là tia đối của tia AB thì ba góc BAD, DAC, CAx có cùng số đo 60º.

Hạ EH ⏊ Bx, EI ⏊ AD, EK ⏊ BC.

Ta có: Vì BE là phân giác góc ABC nên suy ra EH = EK (Áp dụng định lí 2).

Vì AE là phân giác góc DAx nên suy ra EH = EI (Áp dụng định lí 2).

Suy ra EK = EI hay E nằm trên tia phân giác của ADC.

Vậy suy ra DE là đường phân giác của góc ADC (đpcm).

Bài 9.18 trang 55 SBT Toán 7 Tập 2: Cho tam giác ABC với M là trung điểm của BC. Lấy điểm N sao cho C là trung điểm của đoạn thẳng BN. Lấy điểm P sao cho M là trung điểm của đoạn thẳng AP. Chứng minh đường thẳng AC đi qua trung điểm của PN, đường thẳng PC đi qua trung điểm của AN.

Lời giải:

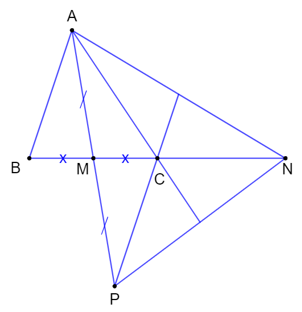
Trong tam giác ANP có đường trung tuyến NM và NC = BC = 2CM nên C là trọng tâm của tam giác ANP.

Do đó AC, PC là hai đường tung tuyến của tam giác ANP.

Vậy AC đi qua trung điểm của PN và PC đi qua trung điểm của AN.