Cho tam giác ABC cân tại A có K là trung điểm của đoạn BC
Lời giải Bài 81 trang 92 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Bài 81 trang 92 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có K là trung điểm của đoạn BC. Hai đường phân giác BD và CE cắt nhau tại I. Chứng minh:
a) I cách đều ba cạnh của tam giác ABC;
b) KI là tia phân giác của góc EKD.
Lời giải
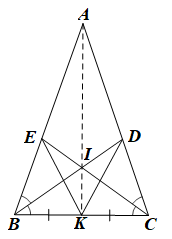
a) Vì ba đường phân giác của tam giác ABC cùng đi qua một điểm nên giao điểm I của hai đường phân giác BD và CE cũng thuộc đường phân giác xuất phát từ đỉnh A của tam giác ABC.
Suy ra I cách đều ba cạnh AB, BC, AC.
Vậy I cách đều ba cạnh của tam giác ABC.
b) • Vì BD là tia phân giác của góc ABC nên .
Vì CE là tia phân giác của góc ACB nên .
Mà (do tam giác ABC cân tại A).
Suy ra .
• Xét ∆ABD và ∆ACE có:
là góc chung,
AB = AC (do tam giác ABC cân tại A),
(chứng minh trên).
Do đó ∆ABD = ∆ACE (g.c.g).
Suy ra AD = AE (hai cạnh góc vuông).
• Xét ∆ABK và ∆ACK có:
AB = AC (chứng minh trên),
AK là cạnh chung,
BK = CK (do K là trung điểm của BC).
Do đó ∆ABK = ∆ACK (c.c.c).
Suy ra (hai góc tương ứng).
Hay .
• Xét ∆AEK và ∆ADK có:
AE = AD (chứng minh trên),
(chứng minh trên),
AK là cạnh chung.
Do đó ∆AEK = ∆ADK (c.g.c)
Suy ra (hai góc tương ứng)
Nên KA là đường phân giác của góc EKD.
Mặt khác do nên AK là tia phân giác của góc BAC.
Mà theo câu a, I thuộc đường phân giác xuất phát từ đỉnh A của tam giác ABC
Nên AI cũng là đường phân giác của góc BAC.
Do vậy, ba điểm A, I, K thẳng hàng.
Khi đó KI cũng là đường phân giác của góc EKD.
Vậy KI là tia phân giác của góc EKD.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
