Cho tam giác ABC (AB < AC). Trên tia phân giác của góc A
Lời giải Bài 79 trang 92 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Giải SBT Toán 7 Cánh diều Bài 11. Tính chất ba đường phân giác của tam giác
Bài 79 trang 92 SBT Toán 7 Tập 2: Cho tam giác ABC (AB < AC). Trên tia phân giác của góc A, lấy điểm E nằm trong tam giác ABC sao cho E cách đều hai cạnh AB, BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Điểm E không nằm trên tia phân giác của góc B.
b) ^EBC=^ECB.
c) Điểm E cách đều AB, BC, CA.
d) Điểm E nằm trên tia phân giác của góc C.
Lời giải
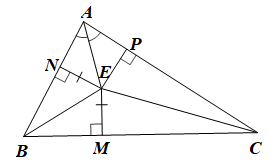
Gọi M, N, P lần lượt là hình chiếu của E trên BC, AB, AC.
Khi đó EM ⊥ BC, EN ⊥ AB, EP ⊥ AC và EN = EM.
• Xét ∆BNE và ∆BME có:
^BNE=^BME(=90°),
EN = EM (giả thiết),
BE là cạnh chung
Do đó ∆BNE = ∆BME (cạnh huyền – cạnh góc vuông)
Suy ra ^NBE=^MBE (hai góc tương ứng)
Nên điểm E nằm trên tia phân giác của góc ABC.
Do đó phát biểu a là sai.
• Vì AF là tia phân giác của góc BAC nên ^BAE=^CAE
Xét ∆ANE và ∆APE có:
^ANE=^APE(=90°),
AE là cạnh chung,
^NAE=^PAE (chứng minh trên).
Do đó ∆ANE = ∆APE (cạnh huyền – góc nhọn).
Suy ra EN = EP (hai cạnh tương ứng).
Mà EN = EM (giả thiết)
Nên EM = EN = EP hay điểm E cách đều ba cạnh AB, BC, CA.
Do đó phát biểu c là đúng.
• Xét hai ∆CPE và ∆CME có:
^CPE=^CME(=90°),
EP = EM (chứng mình trên),
CE là cạnh chung
Do đó ∆CPE = ∆CME (cạnh huyền – cạnh góc vuông)
Suy ra ^PCE=^MCE (hai góc tương ứng).
Nên điểm E nằm trên tia phân giác của góc ACB.
Do đó phát biểu d là đúng.
• Do AB < AC nên ^ACB<^ABC (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn).
Khi đó ^EBC=12^ABC<12^ACB=^ECB.
Do đó phát biểu b là sai.
Vậy a, b là phát biểu sai; c, d là phát biểu đúng.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
