Cho tam giác ABC có góc ABC cộng góc ACB bằng 2 góc BAC
Lời giải Bài 80 trang 92 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.
Giải SBT Toán 7 Cánh diều Bài 11. Tính chất ba đường phân giác của tam giác
Bài 80 trang 92 SBT Toán 7 Tập 2: Cho tam giác ABC có . Hai tia phân giác của góc B và góc C cắt nhau tại K. Trong các phát biểu sau, phát biểu nào sai?
a) Số đo góc KAC bằng 30°.
b) Số đo góc BAK bằng 25°.
c) Số đo góc BKC bằng 120°.
d) Số đo góc BKC bằng 115°.
Lời giải
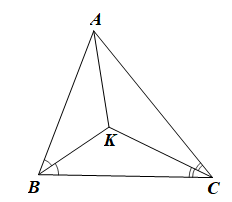
• Xét ABC có (tổng ba góc của một tam giác)
Mà nên
Suy ra
Xét tam giác ABC có hai tia phân giác của góc B và góc C cắt nhau tại K
Nên AK là tia phân giác của góc BAC.
Suy ra
Do đó phát biểu a là đúng, phát biểu b là sai.
• Vì BK là tia phân giác của góc ABC nên
Vì CK là tia phân giác của góc ACB nên
Suy ra
Mà
Do đó
Xét KBC có (tổng ba góc của một tam giác)
Nên .
Do đó phát biểu c là đúng, phát biểu d là sai.
Vậy phát biểu sai là b và d.
Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 12: Tính chất ba đường trung trực của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài 13: Tính chất ba đường cao của tam giác
- Giải Sách bài tập Toán 7 Cánh diều Bài tập cuối chương 7
