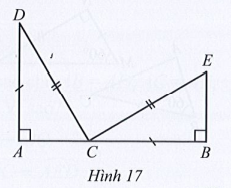
Ở Hình 17 có ba điểm A, B, C thẳng hàng; AD và BE vuông góc với AB; AD = BC; DC = CE

Lời giải Bài 30 trang 75 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

173
« Trang trước
Chia sẻ
Trang sau »
Giải SBT Toán 7 Cánh diều Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 30 trang 75 SBT Toán 7 Tập 2: Ở Hình 17 có ba điểm A, B, C thẳng hàng; AD và BE vuông góc với AB; AD = BC; DC = CE. Chứng minh:

a) ΔDAC = ΔCBE;

b) DCE^=90°.

Sách bài tập Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh  (ảnh 1) 

Lời giải

a) Xét ∆ACD và ∆BEC có:

CAD^=EBC^ (cùng bằng 90°),

CD = CE (giả thiết),

AD = BC (giả thiết).

Do đó ΔDAC = ΔCBE (cạnh huyền – cạnh góc vuông).

Vậy ΔDAC = ΔCBE.

b) Vì ΔDAC = ΔCBE (chứng minh câu a)

Suy ra DCA^=CEB^ (cặp góc tương ứng).

Xét ∆CEB vuông tại B có: CEB^+ECB^=90° (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra DCA^+ECB^=90°

Mặt khác DCA^+DCB^=180°(hai góc kề bù)

Hay DCA^+DCE^+ECB^=180°

Suy ra DCE^=180°−DCA^+ECB^=180°−90°=90°.

Vậy DCE^=90°.

Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:

Bài viết liên quan

173
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao