Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD

Lời giải Bài 28 trang 75 SBT Toán 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

247
« Trang trước
Chia sẻ
Trang sau »
Giải SBT Toán 7 Cánh diều Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 28 trang 75 SBT Toán 7 Tập 2: Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD. Vẽ một phần đường tròn tâm C và tâm D có cùng bán kính, E là điểm chung của hai phần đường tròn đó (E nằm trong góc xOy) (Hình 15).

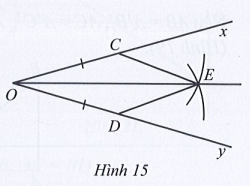
Sách bài tập Toán 7 Bài 4 (Cánh diều): Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh  (ảnh 1) 

Vẽ các đoạn thẳng CE, DE. Chứng minh:

a) ΔOCE = ΔODE;

b) OE là tia phân giác của góc xOy;

c) OCE^=ODE^.

Lời giải

a) Vì E là điểm chung của hai phần đường tròn tâm C, tâm D có cùng bán kính nên EC = ED.

Xét ∆OCE và ∆ODE có:

EC = ED (chứng minh trên),

OC = OD (giả thiết),

OE là cạnh chung.

Suy ra ∆OCE = ∆ODE (c.c.c).

Vậy ∆OCE = ∆ODE.

b) Vì ∆OCE = ∆ODE (chứng minh câu a).

Nên COE^=DOE^ (hai góc tương ứng).

Suy ra OE là tia phân giác của góc xOy.

Vậy OE là tia phân giác của góc xOy.

c) Vì ∆OCE = ∆ODE (chứng minh câu a)

Nên OCE^=ODE^ (hai góc tương ứng).

Vậy OCE^=ODE^.

Xem thêm các bài giải sách bài tập Toán 7 bộ sách Cánh diều hay, chi tiết khác:

Bài viết liên quan

247
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao